圆的反演学习笔记
圆的反演学习笔记
当初集训的时候听老师瞎扯性质，并不知道如何证明，现在也不知道，干脆将性质写下来，以后填坑算了。
1.定义：
假设有一圆c，圆心为o，半径为r，则一点p相对与o的反演点p’满足op*op’=r2
2.性质：
<1>.圆内的点反演后在圆外，圆上的点不变，圆外的点反演后在圆内。
<2>.经过圆心的直线反演后还是一样的直线。
<3>.不经过圆心的直线反演后变成一个过反演中心的圆。
<4>.不过圆心的圆反演后还是一个圆。
<5>.过圆心的圆反演后变成一条不过圆心的直线。
3.应用：
(1).求不过圆心的圆的反演圆：
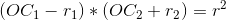
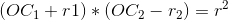
（1）式-（2）式，得：
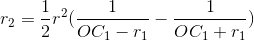
（1）式+（2）式，得：
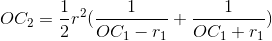
设反演中心坐标为(x0,y0),要反演的圆的圆心坐标为(x1,y1),反演后的圆圆心为(x2,y2)，则:
