虚树
虚树
1.什么时候用(为什么用):
对于某些树,我们并不需要用到全部的点。
如果用全部的点,会超时。
所以,我们将需要用到的点拎出来建树,来确保时间复杂度的优秀。
注:我们所建的虚树就是包含所有需求点,省略某些非需求点的最小连通子图。
如图:
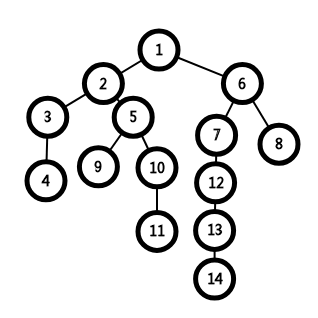
若图中需要用到点4、5、12、14,
我们只需放入1、2、4、5、12、14。
2.如何做:
我们用一个栈来保存一条链上的点。
在不断插入需要用的点的过程中,
设插入的点为u,设链尾与u的lca为t;
则t与这条链 在一条长的链上(t在这条链上 或 t是链首的祖先)。
如果t在这条链中,则深度在t下的点按栈序连边,
将t与第一个深度在t的下的点v连边,将t放在栈中v的位置(栈中不存在t),
将u放在t下一个。
如果t在这条链上,将栈中点按栈序连边,t与栈顶连边,清空栈,t为栈顶,将u放在t下一个。
画个图理解一下:
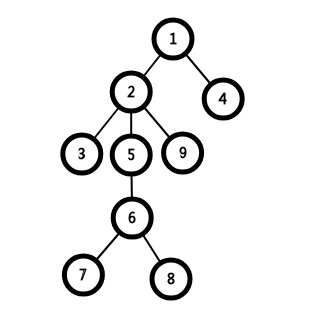
假如,栈中点为:2、6、7,加入的点为4,lca为1,t在链上,2与6连边,6与7连边,1与2连边,1、4放入栈。
假如,栈中点为:1、6、7,加入的点为9,lca为2,t在链中,6与7连边,2与6连边,2、9放入栈。
可以发现,两种情况几乎一模一样。
所以直接上代码:
1 void ins(int u) 2 { 3 if(top==1){s[++top]=u; return;} 4 int t=lca(u,s[top]); 5 if(s[top]==t) return; 6 while(top>1&&d[s[top-1]]>=d[t]) f[s[top-1]].push_back(s[top]),--top; 7 if(t!=s[top]) f[t].push_back(s[top]),s[top]=t; 8 if(t!=u) s[++top]=u; 9 }
3.为什么正确:
若u在栈代表的链中,t=u;
我们会将u以下的点按栈序连边,
u与离它最近的低于它的点连边,u放入栈(u不在栈中)。
栈中依旧为链。
若u不在栈代表的链中:
我们会将t以下的点按栈序连边,
t与离它最近的低于它的点连边,t放入栈(t不在栈中)。
u放入栈。
栈中依旧为链。
注:栈顶的深度只可能不变或变低。最后的栈顶定为虚树的根


