圆方树学习笔记
圆方树
一.是什么:
对于一个连通图,
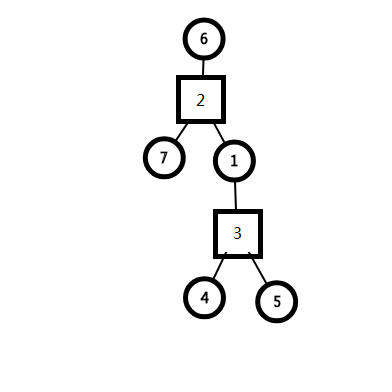
设所有原来的点为圆点,将每个点双连通分量缩成一个方点,与相邻的圆点连边,不存在圆点之间的边。
连接两个方点的圆点都是割点。
二.有什么用:
可以将图上问题转化为树上问题,利用树的优秀性质做题。
将圆点和方点附上合适的权值,可将图的问题转化为树型DP。
三.具体实现:
tarjan求点双,
将父节点和栈中点都与点双连边。
搜索变为有根树(可同时DP)。
四.代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=200006,M=400006; 4 int head[N],head2[N],low[N],dfn[N],siz[N],w[N],n,m; 5 int deep=0,cnt=0,top=0,s[N],t1,t2,num=0; 6 long long ans=0; 7 struct edge 8 { 9 int nxt,to; 10 }e[M<<1],g[M<<1]; 11 //e为原图,g为圆方树的图 12 inline int read() 13 { 14 int T=0,F=1; char ch=getchar(); 15 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 16 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 17 return F*T; 18 }//读入优化 19 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 20 inline void add2(int u,int v){g[++cnt].nxt=head2[u]; g[cnt].to=v; head2[u]=cnt;} 21 void tarjan(int u) 22 { 23 dfn[u]=low[u]=++deep; s[++top]=u; ++num; 24 int t; 25 for(int i=head[u];i,t=e[i].to;i=e[i].nxt) 26 { 27 if(!dfn[t]) 28 { 29 tarjan(t),low[u]=min(low[u],low[t]); 30 if(low[t]>=dfn[u]) 31 { 32 ++n; add2(n,u),add2(u,n); ++w[n]; 33 while(s[top+1]!=t) add2(s[top],n),add2(n,s[top]),++w[n],--top; 34 //add2表示:将点双里的圆点与点双的方点相连 35 } 36 } 37 else low[u]=min(low[u],dfn[t]); 38 } 39 }//tarjan 40 void dfs(int u,int fa) 41 { 42 printf("%d :",u); 43 for(int i=head2[u];i;i=g[i].nxt) if(g[i].to!=fa) printf(" %d",g[i].to); 44 for(int i=head2[u];i;i=g[i].nxt) 45 if(g[i].to!=fa) dfs(g[i].to,u); 46 }//输出圆方树的结构,n为输入的点数,n'为现在的点数 47 //1~n为圆点,n+1~n'为方点 48 int main() 49 { 50 n=read(),m=read(); 51 for(register int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2),add(t2,t1); 52 cnt=0; t1=n; 53 for(register int i=1;i<=t1;++i) if(!dfn[i]) top=0,num=0,tarjan(i),dfs(i,0); 54 return 0; 55 }
五.题目:


