2-SAT学习笔记
2-SAT学习笔记
1.what is:
有一个由n个bool变量组成的序列A,有一定的限制条件,求出满足条件的方案。
2.how to do:
(1).建图:
将每个点拆成(i<<1)和((i<<1)|1)[即 2*i 和 2*i+1 ],分别代表这个变量是真或假。
连接有向边(u->v)表示由u定能推出v。
有几种条件:
<1>.x or y(x|y):
当x为假时,y一定为真;当y为假时,x一定为真。
所以,连接(x<<1)->((y<<1)|1),(y<<1)->((x<<1)|1)。
<2>.x or(not y)(x|(!y)):
当x为假时,y一定为假;当y为真时,x一定为真。
所以,连接(x<<1)->(y<<1),((y<<1)|1)->((x<<1)|1)。
<3>.x xor y(x^y):
当x为假时,y一定为真;当y为假时,x一定为真;
当x为真时,y一定为假;当y为真时,x一定为假;
所以,连接(x<<1)->((y<<1)|1),(y<<1)->((x<<1)|1),
((x<<1)|1)->(y<<1),((y<<1)|1)->(x<<1)。
<4>.x xor (not y)(x^(!y)):
当x为假时,y一定为假;当y为假时,x一定为假;
当x为真时,y一定为真;当y为真时,x一定为真;
所以,连接(x<<1)->(y<<1),(y<<1)->(x<<1),
((x<<1)|1)->((y<<1)|1),((y<<1)|1)->((x<<1)|1)。
(2).判断:
对于一个强连通分量,选其中一个就能推出其它。
所以如果(i<<1)和((i<<1)|1)处在一个强连通分量中,此题无解。
若(i<<1)的强连通分量能推出((i<<1)|1)的强连通分量,选(i<<1)则必选((i<<1)|1),矛盾;所以只能选((i<<1)|1)。
若((i<<1)|1)的强连通分量能推出(i<<1)的强连通分量,反之,只能选(i<<1)。
若(i<<1)的强连通分量和((i<<1)|1)的强连通分量不存在推断关系,任意选择皆可。
所以直接按拓扑序排。
如果(i<<1)的拓扑序大于((i<<1)|1)的拓扑序,选(i<<1);
否则,选((i<<1)|1)。
又因tarjan是按dfs序搜索,所以缩点后的编号是反的拓扑序。
直接按编号比较即可:
如果(i<<1)的拓扑序小(不是“大”)于((i<<1)|1)的拓扑序,选(i<<1);
否则,选((i<<1)|1)。
有人可能会问,“不妨选”的情况难道不会导致错乱?
同级都可选择的(i<<1)和((i<<1)|1)判断是否是玄学。
存不存在都可选择的两点u和v,u选为假,(u<<1)->((v<<1)|1),v却也选为假。
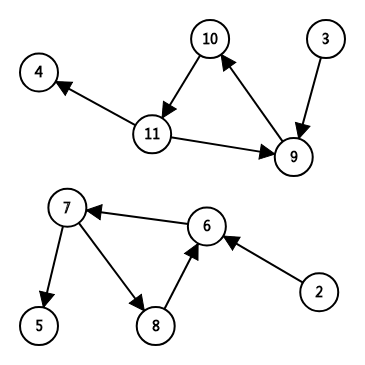
图中,模拟tarjan过程如下:
1>.2:缩点为1;
2>.6、7、8:缩点为2;
3>.5:缩点为3;
4>.3:缩点为4;
5>.9、10、11:缩点为5;
6>.4:缩点为6;
2、3为1的真和假,4、5为2的真和假。
编号:2<3,5<4;
选择2和5,处于同一链上。
即tarjan会先搜处于同一链上的点,所以处于同一链上的点都是大于或小于另一条链的,不存在一个大一个小的情况。
若u选为假,则编号(u<<1)<((u<<1)|1),(u<<1)->((v<<1)|1),则编号((v<<1)|1)<(v<<1)。
(3).代码:
这里,假为i,真为(i+n)。
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=2000006; 5 int head[N],cnt=0,n,m,t1,t2,dfn[N],low[N],num[N],s[N],tot=0,top=0,deep=0,t3,t4; 6 struct edge 7 { 8 int nxt,to; 9 }e[N]; 10 inline int read() 11 { 12 int T=0,F=1; char ch=getchar(); 13 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 14 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 15 return F*T; 16 } 17 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 18 void tarjan(int u) 19 { 20 dfn[u]=low[u]=++deep; s[++top]=u; 21 for(int i=head[u];i;i=e[i].nxt) 22 { 23 if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]); 24 else if(!num[e[i].to]) low[u]=min(low[u],dfn[e[i].to]); 25 } 26 if(dfn[u]==low[u]) 27 { 28 ++tot; num[u]=tot; 29 while(s[top]!=u) num[s[top]]=tot,--top; 30 --top; 31 } 32 } 33 int main() 34 { 35 n=read(),m=read(); 36 for(re int i=1;i<=m;++i) t1=read(),t2=read(),t3=read(),t4=read(),add(t1+(t2^1)*n,t3+t4*n),add(t3+(t4^1)*n,t1+t2*n); cnt=0; 37 //建图 38 n<<=1; 39 for(re int i=1;i<=n;++i) if(!dfn[i]) tarjan(i); memset(dfn,0,sizeof(dfn)); 40 //缩点 41 n>>=1; deep=0; 42 for(re int i=1;i<=n;++i) if(num[i]==num[i+n]){printf("IMPOSSIBLE"); return 0;} 43 //是否真假在同一强连通分量 44 printf("POSSIBLE\n"); 45 for(re int i=1;i<=n;++i) 46 { 47 if(num[i]<num[i+n]) printf("0 "); 48 else printf("1 "); 49 } 50 return 0; 51 }


