tarjan习题题解
tarjan习题
一.割点:
1.模板:
洛谷P3388 【模板】割点(割顶)
题目背景
割点
题目描述
给出一个n个点,m条边的无向图,求图的割点。
输入输出格式
输入格式:
第一行输入n,m
下面m行每行输入x,y;x,y表示x到y有一条边
输出格式:
第一行输出割点个数
第二行按照节点编号从小到大输出节点,用空格隔开
输入输出样例
输入样例#1:
6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6
输出样例#1:
1
5
说明
对于全部数据n≤20000,m≤100000
点的编号均大于0小于等于n。
tarjan图不一定联通。
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=20006,M=200006; 5 int n,m,low[N],head[N],dfn[N],deep=0,cnt=0,is_cut[N],t1,t2,tot=0; 6 struct edge 7 { 8 int nxt,to; 9 }e[M]; 10 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 11 inline int read() 12 { 13 int T=0,F=1; char ch=getchar(); 14 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 15 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 16 return F*T; 17 } 18 void tarjan(int u,int fa) 19 { 20 dfn[u]=low[u]=++deep; int num=0,v; 21 for(int i=head[u];i;i=e[i].nxt) 22 { 23 v=e[i].to; 24 if(!dfn[v]) 25 { 26 ++num,tarjan(v,u),low[u]=min(low[u],low[v]); 27 if(fa&&low[v]>=dfn[u]) is_cut[u]=1; 28 } 29 else low[u]=min(low[u],dfn[v]); 30 } 31 if(!fa&&num>=2) is_cut[u]=1; 32 } 33 int main() 34 { 35 n=read(); m=read(); 36 for(re int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2),add(t2,t1); 37 for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0); 38 for(int i=1;i<=n;++i) if(is_cut[i]) ++tot; 39 printf("%d\n",tot); 40 for(int i=1;i<=n;++i) if(is_cut[i]) printf("%d ",i); 41 return 0; 42 }
2.矿场搭建:
洛谷P3225 [HNOI2012]矿场搭建
题目描述
煤矿工地可以看成是由隧道连接挖煤点组成的无向图。为安全起见,希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口,使得无论哪一个挖煤点坍塌之后,其他挖煤点的工人都有一条道路通向救援出口。
请写一个程序,用来计算至少需要设置几个救援出口,以及不同最少救援出口的设置方案总数。
输入输出格式
输入格式:
输入文件有若干组数据,每组数据的第一行是一个正整数 N(N<=500),表示工地的隧道数,接下来的 N 行每行是用空格隔开的两个整数 S 和 T,表示挖 S 与挖煤点 T 由隧道直接连接。输入数据以 0 结尾。
输出格式:
输入文件中有多少组数据,输出文件 output.txt 中就有多少行。每行对应一组输入数据的 结果。
其中第 i 行以 Case i: 开始(注意大小写,Case 与 i 之间有空格,i 与之间无空格,之后有空格),
其后是用空格隔开的两个正整数,第一个正整数表示对于第 i 组输入数据至少需 要设置几个救援出口,
第二个正整数表示对于第 i 组输入数据不同最少救援出口的设置方案总 数。输入数据保证答案小于 2^64。
输出格式参照以下输入输出样例。
输入输出样例
输入样例#1:
9
1 3
4 1
3 5
1 2
2 6
1 5
6 3
1 6
3 2
6
1 2
1 3
2 4
2 5
3 6
3 7
0
输出样例#1:
Case 1: 2 4
Case 2: 4 1
说明
Case 1 的四组解分别是(2,4),(3,4),(4,5),(4,6);
Case 2 的一组解为(4,5,6,7)。
一句话题意:
给出一个n个点、m条边的无向连通图,设置一些点使删除任意一个点后,剩下的点互相连通。
求这些点最少有多少个,最少的方案有多少种。
思路:
非割点删除时,整个连通块仍然连通;
删割点时,因为每次只删一个,
所以若包含它的点双连通分量不止一个割点(即这个点双连通分量与至少两个点双连通分量相连),删去这个割点后仍能到达其它点双连通分量的救援出口,无影响;
若只有一个割点,便要在自己里设一个救援出口。
最后要特判只有一个点双连通分量的情况,
若救援出口坍塌,所有人要能转移到另一个救援出口,故要设立两个。
另外,思路之所以正确,是因为不存在所有点都至少有两个割点的情况,那样就只有一个点双连通分量。
代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=506; 4 int n,m,cnt=0,head[N],dfn[N],low[N],cut[N],deep=0,fa,t1,t2,d[N],s[N],top,tot,siz[N],num[N][N],p=0; 5 long long ans=0; 6 struct edge 7 { 8 int nxt,to; 9 }e[N*2]; 10 inline int read() 11 { 12 int T=0,F=1; char ch=getchar(); 13 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 14 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 15 return T*F; 16 } 17 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 18 void tarjan(int u) 19 { 20 dfn[u]=low[u]=++deep; s[++top]=u; int o=0; 21 for(int i=head[u];i;i=e[i].nxt) 22 { 23 if(!dfn[e[i].to]) 24 { 25 ++o; 26 tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]); 27 if(low[e[i].to]>=dfn[u]) 28 { 29 if(u!=fa) cut[u]=1; ++tot; 30 while(s[top]!=u) num[tot][++siz[tot]]=s[top],--top; 31 num[tot][++siz[tot]]=s[top]; 32 //求出点双连通分量中的所有点 33 } 34 } 35 else low[u]=min(low[u],dfn[e[i].to]); 36 } 37 if(u==fa&&o>=2) cut[u]=1; 38 } 39 int main() 40 { 41 m=read(); 42 while(m) 43 { 44 tot=cnt=deep=top=n=0; ans=1; memset(head,0,sizeof(head)); memset(low,0,sizeof(low)); memset(dfn,0,sizeof(dfn)); 45 memset(cut,0,sizeof(cut)); memset(d,0,sizeof(d)); memset(siz,0,sizeof(siz)); memset(num,0,sizeof(num)); 46 //赋初值 47 for(int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2),add(t2,t1),n=max(n,max(t1,t2)); 48 //连边 49 for(int i=1;i<=n;++i) if(!dfn[i]) fa=i,tarjan(i); 50 //tarjan求点双连通分量 51 cnt=0; ++p; 52 for(int i=1;i<=tot;++i) 53 { 54 deep=0; 55 for(int j=1;j<=siz[i];++j) 56 if(cut[num[i][j]]) ++deep; 57 //求割点数deep 58 if(deep==1) ++cnt,ans*=(siz[i]-1); 59 } 60 if(tot==1) cnt=2,ans=n*(n-1)/2; 61 //特判 62 printf("Case %d: %d %lld\n",p,cnt,ans); 63 m=read(); 64 } 65 return 0; 66 }
3.BLO:
洛谷P3469 [POI2008]BLO-Blockade
题目描述
在Byteotia有n个城镇。 一些城镇之间由无向边连接。 在城镇外没有十字路口,尽管可能有桥,隧道或者高架公路(反正不考虑这些)。每两个城镇之间至多只有一条直接连接的道路。人们可以从任意一个城镇直接或间接到达另一个城镇。 每个城镇都有一个公民,他们被孤独所困扰。事实证明,每个公民都想拜访其他所有公民一次(在主人所在的城镇)。所以,一共会有n*(n-1)次拜访。
不幸的是,一个程序员总罢工正在进行中,那些程序员迫切要求购买某个软件。
作为抗议行动,程序员们计划封锁一些城镇,阻止人们进入,离开或者路过那里。
正如我们所说,他们正在讨论选择哪些城镇会导致最严重的后果。
编写一个程序:
读入Byteotia的道路系统,对于每个被决定的城镇,如果它被封锁,有多少访问不会发生,输出结果。
输入输出格式
第一行读入n,m,分别是城镇数目和道路数目
城镇编号1~n
接下来m行每行两个数字a,b,表示a和b之间有有一条无向边
输出n行,每行一个数字,为第i个城镇被锁时不能发生的访问的数量。
输入输出样例
输入样例#1:
5 5
1 2
2 3
1 3
3 4
4 5
输出样例#1:
8
8
16
14
8
一句话题意:
给出一个n个点、m条边的无向连通图,
求删除每个点后,不能连通的点对有多少个。
注:(i,j)和(j,i) (i!=j)算两个点对,被删除的点也算进点对。
思路:
对于每个点:
若不是割点,所有点不能到此点,共有(n-1)*1*2个点对不连通;
若是割点,可看作本身一个连通块,所有low[v]>=dfn[u](u:此点,v:儿子)的儿子各看作一个连通块,父亲和其它儿子看作一个连通块,
删去后,所有连通块互相不能到达。
所以答案即为:所有low[v]>=dfn[u]的子连通块的size[v]*(n-size[v]<v的子节点个数>*2(双向)+u到父辈们的u*(n-sum-1)*2(双向;sum为所有low[v]>=dfn[u]的子连通块的size(子节点个数)和)
代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=100006,M=500006; 4 int head[N],cnt=0,n,m,t1,t2,dfn[N],low[N],is_cut[N],tot=0,top=0,deep=0; 5 long long ans[N],num[N]; 6 struct edge 7 { 8 int nxt,to; 9 }e[M*2]; 10 inline int read() 11 { 12 int T=0,F=1; char ch=getchar(); 13 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 14 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 15 return F*T; 16 } 17 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 18 void tarjan(int u) 19 { 20 dfn[u]=low[u]=++deep; int o=0; num[u]=1; 21 long long sum=0; 22 for(int i=head[u];i;i=e[i].nxt) 23 { 24 if(!dfn[e[i].to]) 25 { 26 ++o; 27 tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]),num[u]+=num[e[i].to]; 28 if((low[e[i].to]>=dfn[u]&&u!=t1)||(u==t1&&o>=2)) is_cut[u]=1; 29 //判断割点 30 if(low[e[i].to]>=dfn[u]) sum+=num[e[i].to],ans[u]+=num[e[i].to]*(n-num[e[i].to]); 31 //求size和 32 } 33 else low[u]=min(low[u],dfn[e[i].to]); 34 } 35 if(is_cut[u]) ans[u]+=(n-sum-1)*(sum+1)+(n-1); 36 //统计答案 37 } 38 int main() 39 { 40 n=read(),m=read(); 41 for(int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2),add(t2,t1); cnt=0; 42 //连边 43 for(int i=1;i<=n;++i) if(!dfn[i]) t1=i,tarjan(i); 44 for(int i=1;i<=n;++i) 45 { 46 if(is_cut[i]) printf("%lld\n",ans[i]); 47 else printf("%d\n",(n-1)*2); 48 } 49 return 0; 50 }
二.桥:
1.桐桐的糖果计划:
vijos P1325桐桐的糖果计划
题目描述
桐桐很喜欢吃棒棒糖。他家处在一大堆糖果店的附近。 但是,他们家的区域经常出现塞车、塞人等情况,这导致他不得不等到塞的车或人走光了他才能去买到他最爱吃的棒棒糖品种。于是,他去找市长帮他修路,使得每两个糖果店之间至少有两条完全不同的路。可是市长经费有限,于是让桐桐找出哪些路被塞住后会使某些糖果店与糖果店间无法到达及最少的修路条数。
你能帮助他吃到他最喜爱的糖果吗?
注:1-> 3-> 2 和 1-> 3-> 4-> 2 为不完全不同的路,即不符合题意的路。
1-> 3-> 4-> 2 和 1-> 5-> 2 为完全不同的路,即符合题意的路。
输入
输入第一行是两个数n,m(n< =5000,m< =10000) 接下来的m行,每行两个数i,j,表示i,j间有一条边连接。
输出
输出有两行。第一行为塞住后就不可以到达某些糖果店的道路条数,第二行为最少的修路条数。
样例输入
7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7
样例输出
3
2
一句话题意:
无向连通图,求桥的个数,并求加多少条边后整张图连通且无桥。
思路:
将度数为1的边双连通分量互连,
度数大于等于2的边双连通分量在度数为1的边双连通分量连接后也互连。
简单来讲,将边双连通分量缩点,图就变成了一棵树,将所有叶子结点互连(叶子结点个数为奇数就将剩下的一个点随便连)后就满足条件。
如:
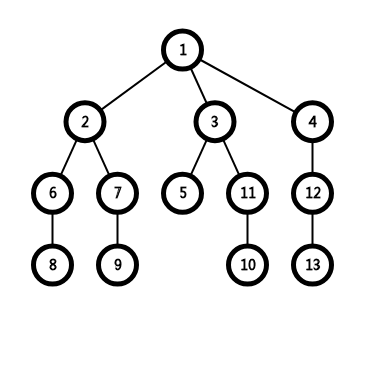
变成:
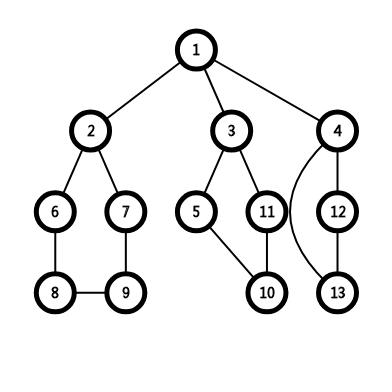
代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=5006,M=10006; 4 int head[N],cnt=1,n,m,t1,t2,dfn[N],low[N],deep=0,v[M*2],f[N],tot=0,d[N],g[N],book[N],p=0; 5 map<int,int> ha[N]; 6 int getf(int u){return g[u]==u?u:g[u]=getf(g[u]);} 7 void merge(int u,int v) 8 { 9 u=getf(u); v=getf(v); 10 if(u==v) return; 11 g[u]=v; 12 } 13 struct edge 14 { 15 int nxt,to; 16 }e[M*2]; 17 inline int read() 18 { 19 int T=0,F=1; char ch=getchar(); 20 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 21 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 22 return F*T; 23 } 24 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 25 void tarjan(int u) 26 { 27 dfn[u]=low[u]=++deep; 28 for(int i=head[u];i;i=e[i].nxt) 29 { 30 if(v[i^1]||v[i]) continue; 31 if(!dfn[e[i].to]) v[i]=1,f[e[i].to]=u,tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]); 32 else low[u]=min(low[u],dfn[e[i].to]); 33 } 34 } 35 int main() 36 { 37 n=read(),m=read(); 38 for(int i=1;i<=n;++i) g[i]=i; 39 for(int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2),add(t2,t1); 40 for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i); 41 for(int i=1;i<=n;++i) if(f[i]&&low[i]>dfn[f[i]]) ++tot,ha[i][f[i]]=1,ha[f[i]][i]=1; 42 //判桥 43 for(int i=1;i<=n;++i) 44 for(int j=head[i];j;j=e[j].nxt) if(ha[i].find(e[j].to)==ha[i].end()) merge(i,e[j].to); 45 cnt=0; 46 for(int i=1;i<=n;++i) g[i]=getf(i);//并查集判所属的边双连通分量 47 for(int i=1;i<=n;++i) 48 if(f[i]&&low[i]>dfn[f[i]]) ++d[g[i]],++d[g[f[i]]];//求度数 49 for(int i=1;i<=n;++i) if(d[i]==1) ++cnt;//求叶子结点个数 50 printf("%d\n%d",tot,(cnt+1)/2); 51 return 0; 52 }
三.缩点(强连通分量)
1.软件安装:
洛谷P2515 [HAOI2010]软件安装
题目描述
现在我们的手头有N个软件,对于一个软件i,它要占用wi磁盘空间,它的价值为vi。我们希望从中选择一些软件安装到一台磁盘容量为M计算机上,使得这些软件的价值尽可能大(即vi的和最大)。
但是现在有个问题:软件之间存在依赖关系,即软件i只有在安装了软件j(包括软件j的直接或间接依赖)的情况下才能正确工作(软件i依赖软件j)。幸运的是,一个软件最多依赖另外一个软件。如果一个软件不能正常工作,那么它能够发挥的作用为0。
我们现在知道了软件之间的依赖关系:软件i依赖软件di 。
现在请你设计出一种方案,安装价值尽量大的软件。一个软件只能被安装一次,如果一个软件没有依赖则di=0,这时只要这个软件安装了,它就能正常工作。
输入输出格式
输入格式:
第1行:N,M(0<=N<=100, 0<= M<= 500)
第2行:w1,w2,w3,…,wn (0<=wi<=M)
第3行:v1,v2,v3,…,vn (0<=vi<=1000)
第4行:d1,d2,d3,…,dn (0<=di<=M,di!=i)
输出格式:
一个整数,代表最大价值
输入输出样例
输入样例#1:
3 10
5 5 6
2 3 4
0 1 1
输出样例#1:
5
一句话题意:
n个点、小于等于n条有向边,每个点都只有一条入边,有的点不存在入边,不存在自环。
每个点都有代价和权值,每一条边i到j表示必须选i才能选j。
如何选点使小于等于m的代价下权值最大,且权值为多少?
思路:
对于构成一个强连通分量的点,选一个就必须选全部,代价和权值都为所有点的和。
想到缩点。
缩完点后的图是一个森林,且只有选父亲才能选儿子,容易想到树型DP。
建立一个虚点作为根,连接所有入度为0的点,用树型背包即可。
代码:
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=1006,M=1006; 5 int n,m,deep=0,cnt=0,tot=0,top=0,t; 6 int num[N],dfn[N],low[N],s[N],v[N],head1[N],head2[N],rd[N],w1[N],w2[N],x[N],y[N],ans[106][N]; 7 struct edge 8 { 9 int nxt,to; 10 }e[M],f[M]; 11 inline void add(int u,int v,edge a[],int head[]){a[++cnt].nxt=head[u]; a[cnt].to=v; head[u]=cnt;} 12 inline int read() 13 { 14 int T=0,F=1; char ch=getchar(); 15 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 16 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 17 return F*T; 18 } 19 void tarjan(int u) 20 { 21 dfn[u]=low[u]=++deep; s[++top]=u; v[u]=1; 22 for(int i=head1[u];i;i=e[i].nxt) 23 { 24 if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]); 25 else if(v[e[i].to]) low[u]=min(low[u],low[e[i].to]); 26 } 27 if(dfn[u]==low[u]) 28 { 29 v[u]=0,num[u]=++tot; 30 while(s[top]!=u) num[s[top]]=tot,v[s[top]]=0,--top; 31 --top; 32 } 33 } 34 void dfs(int u) 35 { 36 for(int j=w2[u];j<=m;++j) ans[u][j]=y[u]; 37 for(int i=head2[u];i;i=f[i].nxt) 38 { 39 dfs(f[i].to); 40 for(int j=m;j>=w2[u];--j) for(int k=0;k<=j-w2[u];++k) ans[u][j]=max(ans[u][j],ans[f[i].to][k]+ans[u][j-k]); 41 } 42 }//树型背包 43 int main() 44 { 45 n=read(),m=read(); 46 for(int i=1;i<=n;++i) w1[i]=read(); 47 for(int i=1;i<=n;++i) x[i]=read(); 48 for(int i=1;i<=n;++i){t=read(); if(t) add(t,i,e,head1);}//建图 49 for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);//tarjan求强连通分量 50 cnt=0; 51 for(int i=1;i<=n;++i) 52 { 53 w2[num[i]]+=w1[i]; y[num[i]]+=x[i]; 54 for(int j=head1[i];j;j=e[j].nxt) if(num[i]!=num[e[j].to]) add(num[i],num[e[j].to],f,head2),++rd[num[e[j].to]]; 55 }//建缩完点后的图 ,并求好每个强连通分量的代价和权值 56 for(int i=1;i<=tot;++i) if(!rd[i]) add(tot+1,i,f,head2); 57 dfs(tot+1);//虚点为tot+1 58 printf("%d",ans[tot+1][m]); 59 return 0; 60 }
2.有机化学之神偶尔会做作弊:
洛谷P2783 有机化学之神偶尔会做作弊
题目背景
XS中学化学竞赛组教练是一个酷爱炉石的人。
有一天他一边搓炉石一边监考,而你作为一个信息竞赛的大神也来凑热闹。
然而你的化竞基友却向你求助了。
“第1354题怎么做”<--手语 他问道。
题目描述
你翻到那一题:给定一个烃,只含有单键(给初中生的一个理解性解释:就是一堆碳用横线连起来,横线都是单条的)。
然后炎魔之王拉格纳罗斯用他的火焰净化了一切环(???)。所有的环状碳都变成了一个碳。如图所示。
然后指定多组碳,求出它们之间总共有多少碳。如图所示(和上图没有关系)。
但是因为在考试,所以你只能把这个答案用手语告诉你的基友。你决定用二进制来表示最后的答案。如图所示(不要在意,和题目没有什么没关系)。
输入输出格式
输入格式:
第一行两个整数n,m.表示有n个点,m根键
接下来m行每行两个整数u,v表示u号碳和v号碳有一根键
接下来一个整数tot表示询问次数
接下来tot行每行两个整数,a,b表示询问的两个碳的编号
输出格式:
共tot行
每行一个二进制数
输入输出样例
输入样例#1:
3 2
1 2
2 3
2
1 2
2 3
输出样例#1:
10
10
说明
1<n<=10000,1<m<=50000
(两个碳不成环)
一句话题意:
n个点、2m条边的有向图,将每个强连通分量缩为一个点,求缩点后的两个点之间的距离。
思路:
水题,假黑题。
很明显的缩点,缩完后就成了一个DAG,形成一棵树。
求树上的距离,lca啊。
水,水,水,水,水……
注意:1.题目中的边要看作无向的,连正向和反向。
2.两个点不成一个强连通分量。
代码:
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=10006,M=100006; 5 int n,m,deep=0,cnt=0,tot=0,top=0,t1,t2,t; 6 int num[N],dfn[N],low[N],s[N],v[N],head1[N],head2[N]; 7 int d[N],ff[N][18]; 8 struct edge 9 { 10 int nxt,to; 11 }e[M],f[M]; 12 inline void add(int u,int v,edge a[],int head[]){a[++cnt].nxt=head[u]; a[cnt].to=v; head[u]=cnt;} 13 inline int read() 14 { 15 int T=0,F=1; char ch=getchar(); 16 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 17 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 18 return F*T; 19 } 20 void tarjan(int u,int fa) 21 { 22 dfn[u]=low[u]=++deep; s[++top]=u; v[u]=1; 23 for(int i=head1[u];i;i=e[i].nxt) 24 { 25 if(e[i].to!=fa) 26 { 27 if(!dfn[e[i].to]) tarjan(e[i].to,u),low[u]=min(low[u],low[e[i].to]); 28 else if(v[e[i].to]) low[u]=min(low[u],low[e[i].to]); 29 } 30 } 31 if(dfn[u]==low[u]) 32 { 33 v[u]=0,num[u]=++tot; 34 while(s[top]!=u) num[s[top]]=tot,v[s[top]]=0,--top; 35 --top; 36 } 37 } 38 void dfs(int u,int fa) 39 { 40 d[u]=d[fa]+1; ff[u][0]=fa; 41 for(int i=1;i<=15;++i) ff[u][i]=ff[ff[u][i-1]][i-1]; 42 for(int i=head2[u];i;i=f[i].nxt) if(f[i].to!=fa) dfs(f[i].to,u); 43 } 44 inline int lca(int l,int r) 45 { 46 if(d[l]<d[r]) swap(l,r); 47 for(int i=15;i>=0;--i) if(d[r]+(1<<i)<=d[l]) l=ff[l][i]; 48 if(l==r) return l; 49 for(int i=15;i>=0;--i) 50 { 51 if(ff[l][i]==ff[r][i]) continue; 52 l=ff[l][i],r=ff[r][i]; 53 } 54 return ff[l][0]; 55 } 56 int main() 57 { 58 n=read(),m=read(); 59 for(int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2,e,head1),add(t2,t1,e,head1); 60 for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0); 61 cnt=0; 62 for(int i=1;i<=n;++i) 63 for(int j=head1[i];j;j=e[j].nxt) if(num[i]!=num[e[j].to]) add(num[i],num[e[j].to],f,head2); 64 dfs(1,0); m=read(); 65 for(re int i=1;i<=m;++i) 66 { 67 t1=read(),t2=read(),t1=num[t1],t2=num[t2]; t=lca(t1,t2); 68 t=d[t1]+d[t2]-d[t]-d[t]+1,cnt=0; 69 while(t) s[++cnt]=(t&1),t>>=1; 70 for(int j=cnt;j>=1;--j) printf("%d",s[j]); 71 printf("\n"); 72 } 73 return 0; 74 }
3.最大半连通子图:
洛谷P2272 [ZJOI2007]最大半连通子图
题目描述
一个有向图G=(V,E)称为半连通的(Semi-Connected),
如果满足:u,v∈V,满足u→v或v→u,即对于图中任意两点u,v,存在一条u到v的有向路径或者从v到u的有向路径。
若G'=(V',E')满足V'∈V,E'是E中所有跟V'有关的边,则称G'是G的一个导出子图。
若G'是G的导出子图,且G'半连通,则称G'为G的半连通子图。
若G'是G所有半连通子图中包含节点数最多的,则称G'是G的最大半连通子图。
给定一个有向图G,请求出G的最大半连通子图拥有的节点数K,以及不同的最大半连通子图的数目C。由于C可能比较大,仅要求输出C对X的余数。
输入输出格式
输入格式:
第一行包含两个整数N,M,X。N,M分别表示图G的点数与边数,X的意义如上文所述接下来M行,每行两个正整数a, b,表示一条有向边(a, b)。图中的每个点将编号为1,2,3…N,保证输入中同一个(a,b)不会出现两次。
输出格式:
应包含两行,第一行包含一个整数K。第二行包含整数C Mod X.
输入输出样例
输入样例#1:
6 6 20070603
1 2
2 1
1 3
2 4
5 6
6 4
输出样例#1:
3
3
说明
对于100%的数据,N<=100000, M<=1000000, X<=10^8
一句话题意:
没有什么好精简的,自己滚去看题。
思路:
首先,对于一个强连通分量,肯定能选就选。
缩点。
然后对于缩完点后的图,任意两点间要半连通,
所以肯定不存在这种情况:
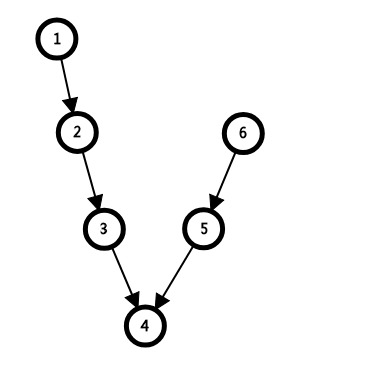
5、6点和1、2、3、4点不半连通。
所以,就是求缩点后最长链(所含点的个数最多)的大小和方案数了。
拓扑DP。
代码:
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=100006,M=1000006; 5 int n,m,deep=0,cnt=0,tot=0,top=0,t1,t2; 6 int num[N],dfn[N],low[N],s[N],v[N],head1[N],head2[N],rd[N]; 7 long long ans[N],maxa=-1,x,sum=0; 8 struct edge 9 { 10 int nxt,to; 11 }e[M],f[M]; 12 inline void add(int u,int v,edge a[],int head[]){a[++cnt].nxt=head[u]; a[cnt].to=v; head[u]=cnt;} 13 inline int read() 14 { 15 int T=0,F=1; char ch=getchar(); 16 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 17 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 18 return F*T; 19 } 20 void tarjan(int u) 21 { 22 dfn[u]=low[u]=++deep; s[++top]=u; v[u]=1; 23 for(int i=head1[u];i;i=e[i].nxt) 24 { 25 if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]); 26 else if(v[e[i].to]) low[u]=min(low[u],low[e[i].to]); 27 } 28 if(dfn[u]==low[u]) 29 { 30 v[u]=0,num[u]=++tot; 31 while(s[top]!=u) num[s[top]]=tot,v[s[top]]=0,--top; 32 --top; 33 } 34 } 35 void tppx() 36 { 37 queue<int> q; int tmp; 38 for(int i=1;i<=tot;++i) if(!rd[i]) ans[i]=1,v[i]=s[i],q.push(i); 39 while(!q.empty()) 40 { 41 tmp=q.front(),q.pop(); 42 if(maxa<v[tmp]) maxa=v[tmp],sum=ans[tmp]; 43 //v数组代表从入度为0的点到此点的节点数 44 //ans数组代表到此点长度为v的方案数 45 else if(maxa==v[tmp]) sum=(sum+ans[tmp])%x; 46 for(int i=head2[tmp];i;i=f[i].nxt) 47 { 48 if(!num[f[i].to]) 49 { 50 num[f[i].to]=1; 51 if(v[f[i].to]<v[tmp]+s[f[i].to]) v[f[i].to]=v[tmp]+s[f[i].to],ans[f[i].to]=ans[tmp]; 52 else if(v[f[i].to]==v[tmp]+s[f[i].to]) ans[f[i].to]=(ans[f[i].to]+ans[tmp])%x; 53 } 54 --rd[f[i].to]; 55 if(!rd[f[i].to]) q.push(f[i].to); 56 } 57 for(int i=head2[tmp];i;i=f[i].nxt) num[f[i].to]=0; 58 } 59 } 60 int main() 61 { 62 n=read(),m=read(),x=read(); 63 for(re int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2,e,head1); 64 for(re int i=1;i<=n;++i) if(!dfn[i]) tarjan(i); 65 memset(s,0,sizeof(s)); memset(v,0,sizeof(v)); 66 cnt=0; 67 for(re int i=1;i<=n;++i) 68 { 69 ++s[num[i]];//这个强连通分量包含的结点数 70 for(int j=head1[i];j;j=e[j].nxt) if(num[i]!=num[e[j].to]) add(num[i],num[e[j].to],f,head2),++rd[num[e[j].to]]; 71 } 72 memset(num,0,sizeof(num)); 73 tppx(); 74 printf("%lld\n%lld\n",maxa,sum); 75 return 0; 76 }
4.草鉴定:
洛谷P3119 [USACO15JAN]草鉴定Grass Cownoisseur
题目描述
约翰有n块草场,编号1到n,这些草场由若干条单行道相连。
奶牛贝西是美味牧草的鉴赏家,她想到达尽可能多的草场去品尝牧草。
贝西总是从1号草场出发,最后回到1号草场。
她想经过尽可能多的草场,贝西在通一个草场只吃一次草,所以一个草场可以经过多次。
因为草场是单行道连接,这给贝西的品鉴工作带来了很大的不便,贝西想偷偷逆向行走一次,但最多只能有一次逆行。
问,贝西最多能吃到多少个草场的牧草。
输入输出格式
输入:
第一行:草场数n,道路数m。
以下m行,每行x和y表明有x到y的单向边,不会有重复的道路出现。
输出:
一个数,逆行一次最多可以走几个草场。
输入输出样例
输入样例#1:
7 10
1 2
3 1
2 5
2 4
3 7
3 5
3 6
6 5
7 2
4 7
输出样例#1:
6
一句话题意:
n个点、m条边的有向图,求加一条反向边后,含1的强连通分量的最大点数。
思路:
对于在一个强连通分量的点,都能吃到。
缩点。
我们一定是加一条边使缩点后的图的一条链变成环。
设含1的强连通分量的编号为t
即找出含t且链首尾存在反向边的最长链。
蛇皮最长路求出从t到每个强连通分量的最大点数之和
满足条件的最长链一端在正图所能跑到的点,
另一端在反图跑到的点
判断两图之间是否有反向边,更新答案。
代码:
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=1e5+8,M=100006; 5 int n,m,dis[N][2],w[N],cnt=1,t2,t1,num[N],head2[N],head[N]; 6 int dfn[N],low[N],s[N],top=0,deep=0,tot=0,book[N],ans=0; 7 struct edge 8 { 9 int nxt,to; 10 }e[M],g[M*2]; 11 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 12 inline void add2(int u,int v){g[++cnt].nxt=head2[u]; g[cnt].to=v; head2[u]=cnt;} 13 inline int read() 14 { 15 int F=1,T=0; char ch=getchar(); 16 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 17 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 18 return F*T; 19 } 20 void tarjan(int u) 21 { 22 dfn[u]=low[u]=++deep; s[++top]=u; int v; 23 for(int i=head[u];i;i=e[i].nxt) 24 { 25 v=e[i].to; 26 if(!dfn[v]) tarjan(v),low[u]=min(low[u],low[v]); 27 else if(!num[e[i].to]) low[u]=min(low[u],dfn[v]); 28 } 29 if(dfn[u]==low[u]) 30 { 31 ++tot; w[tot]=1; num[u]=tot; 32 while(s[top]!=u) num[s[top]]=tot,++w[tot],--top; 33 --top; 34 } 35 } 36 void spfa(int u,int v) 37 { 38 dis[u][v]=w[u]; 39 queue<int> q; q.push(u); book[u]=1; 40 while(!q.empty()) 41 { 42 int tmp=q.front(); q.pop(); 43 for(int i=head2[tmp];i;i=g[i].nxt) 44 { 45 if((i&1)!=v) continue; 46 if(dis[g[i].to][v]<dis[tmp][v]+w[g[i].to]) 47 { 48 dis[g[i].to][v]=dis[tmp][v]+w[g[i].to]; 49 if(!book[g[i].to]) book[g[i].to]=1,q.push(g[i].to); 50 } 51 } 52 book[tmp]=0; 53 } 54 } 55 void dfs(int u) 56 { 57 book[u]=1; 58 for(int i=head2[u];i;i=g[i].nxt) 59 { 60 if(dis[u][0]&&dis[g[i].to][1]) ans=max(ans,dis[g[i].to][1]+dis[u][0]); 61 if((i&1)) continue; 62 if(!book[g[i].to]) dfs(g[i].to); 63 } 64 } 65 int main() 66 { 67 n=read(),m=read(); 68 for(re int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2); cnt=1;//注意!cnt从1开始 69 for(re int i=1;i<=n;++i) if(!dfn[i]) deep=top=0,tarjan(i); 70 for(re int i=1;i<=n;++i) for(int j=head[i];j;j=e[j].nxt) if(num[i]!=num[e[j].to]) add2(num[i],num[e[j].to]),add2(num[e[j].to],num[i]); 71 //正图边的编号是2的倍数,反图编号不是2的倍数 72 spfa(num[1],0);//跑正图 73 spfa(num[1],1);//跑反图 74 dfs(num[1]);//跑正图看是否有反向边 75 printf("%d\n",ans-w[num[1]]);//dis正反图都包含了w[num[1]] 76 return 0; 77 }
5.逛庭院:
洛谷P5008 逛庭院
题目背景
你在尘世中辗转了千百年
却只让我看你最后一眼
火光描摹容颜燃尽了时间
别留我一人,孑然一身
凋零在梦境里面。
——《银临&云の泣·锦鲤抄》
题目描述
这首歌的文案如下:(注:不阅读文案不影响下面的阅读)
宁武皇仁光九年锦文轩刻本《异闻录》载:
扶桑画师浅溪,居泰安,喜绘鲤。
院前一方荷塘,锦鲤游曳,溪常与嬉戏。
其时正武德之乱,藩镇割据,战事频仍,魑魅魍魉,肆逆于道。
兵戈逼泰安,街邻皆逃亡,独溪不舍锦鲤,未去。
是夜,院室倏火。
有人入火护溪,言其本鲤中妖,欲取溪命,却生情愫,遂不忍为之。
翌日天明,火势渐歇,人已不见。
溪始觉如梦,奔塘边,但见池水干涸,莲叶皆枯,塘中鲤亦不知所踪。
自始至终,未辨眉目,只记襟上层迭莲花,其色魅惑,似血着泪。
后有青岩居士闻之,叹曰:魑祟动情,必作灰飞。犹蛾之投火耳,非愚,乃命数也。
以下是题面内容
扶苏被画师和锦鲤的故事深深地打动了。为了能让锦鲤和画师继续生活在一起,他决定回到着火的庭院中灭掉大火。
画师的庭院可以抽象成一个有向图,每个点代表着一个着火的位置。
为了量化火势的大小,扶苏给每个点一个火力值,火力值越大,代表这个点的火势越强。
风助火势,火借风力,对于每一个着火点,都有可能因为大风使得火扩散到其他点。
有向图的每条边<u,v>代表大火是从点u扩散到点v的。
需要注意的是一个点可能会扩散到很多点,也可能是由很多点的大火一起扩散成的。
为了不因为灭掉火源让画师发现有人在帮他灭火,在任意时刻,扶苏不能灭掉任何一个不被任何点所扩散的点的火。
一个点的火被灭掉后,所代表该点的火扩散的所有边将消失。
需要说明的是,虽然边消失了,但是该点扩散到的所有点属性除入度以外都不会改变,更不会消失。
因为穿越的时间有限,扶苏只能灭掉最多k个点的火。
因为他菜的马上就要退役了所以他不知道最优方案是什么。
于是他想问问你他最多能扑灭多少火力值。
说人话:
给你一张有向图,每个点有一个点权。你可以任意选择一个有入度的点,获得它的点权并把它和它的出边从图上删去。任意时刻不能选择没有入度的点。最多能选择k个点,求最多能获得多少点权。
输入输出格式
输入格式:
输入的第一行是两个数n,m,k,代表图的点数和边数以及点数的限制
输入的第二行是n个整数,第i个数代表点i的火力值(点权)
下面mm行每行两个数u,v,代表一条由u指向v的有向边
输出格式:
输出的第一行一个整数,代表最大的火力值
输入输出样例
输入样例#1:
7 7 3
10 2 8 4 9 5 7
1 2
1 3
1 4
2 5
3 6
3 7
4 7
输出样例#1:
24
说明
本题采用多测试点捆绑测试。
各测试点数据范围与约定如下图所示
一句话题意:
n个点、m条边的有向图,你有k次选择点的机会,使所选点的权值最大,问最大多少。
每次选择的点入度不为0,并要删除此点和所有与其相连的边。
思路:
有向图->缩点和拓扑排序
看题:缩点 拓扑排序
缩点。
设原图为G,现图为G’。
则G’中入度为0的点中定有任意一点不能选择。
如图:
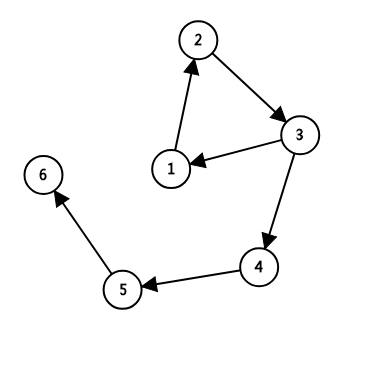
贪心地想,肯定不选点权最小的,标记它。
G’中入度不为0的点中都能选择。
如图:
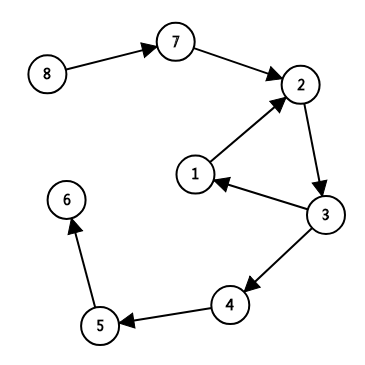
可以按3、1、2的顺序选择。
最后按点权排序,除标记的点外的前k个。
最后说一句,银临大大的歌敲好听的啦,有兴趣的同学可以听听《锦鲤抄》。
代码:
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=5e5+6,M=2e6+6; 5 int n,m,cnt=0,head[N],t1,t2,top=0,deep=0,tot=0,t; 6 int dfn[N],low[N],num[N],s[N],rd[N],w[N],k,ans=0; 7 struct edge 8 { 9 int nxt,to; 10 }e[M]; 11 struct xd{int x,i;}a[N]; 12 inline int read() 13 { 14 int T=0,F=1; char ch=getchar(); 15 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 16 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 17 return F*T; 18 } 19 inline void add1(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 20 void tarjan(int u) 21 { 22 dfn[u]=low[u]=++deep; s[++top]=u; 23 for(int i=head[u];i;i=e[i].nxt) 24 { 25 if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]); 26 else if(!num[e[i].to]) low[u]=min(low[u],dfn[e[i].to]); 27 } 28 if(low[u]==dfn[u]) 29 { 30 ++tot; num[u]=tot; 31 while(s[top]!=u) num[s[top]]=tot,--top; 32 --top; 33 } 34 } 35 bool cmp(xd u,xd v){return u.x>v.x;} 36 int main() 37 { 38 n=read(),m=read(),k=read(); 39 for(re int i=1;i<=n;++i) w[i]=read(),a[i].i=i,a[i].x=w[i]; 40 for(re int i=1;i<=m;++i) t1=read(),t2=read(),add1(t1,t2); cnt=0; 41 for(re int i=1;i<=n;++i) if(!dfn[i]) deep=top=0,tarjan(i); 42 memset(dfn,0x3f,sizeof(dfn)); memset(low,0,sizeof(low)); 43 //dfn代表这个强连通分量的最小点权,low代表最小点权的点的编号 44 for(re int i=1;i<=n;++i) for(int j=head[i];j;j=e[j].nxt) if(num[i]!=num[e[j].to]) ++rd[num[e[j].to]]; 45 for(re int i=1;i<=n;++i) if(!rd[num[i]]) if(dfn[num[i]]>w[i]) dfn[num[i]]=w[i],low[num[i]]=i; 46 sort(a+1,a+n+1,cmp); cnt=0; 47 for(re int i=1;i<=n&&cnt<k;++i) 48 { 49 t=a[i].i; 50 if(low[num[t]]!=t) ++cnt,ans+=w[t]; 51 } 52 printf("%d\n",ans); 53 return 0; 54 }
6.杀人游戏:
洛谷P4819 [中山市选]杀人游戏
题目描述
一位冷血的杀手潜入Na-wiat,并假装成平民。
警察希望能在N个人里面,查出谁是杀手。
警察能够对每一个人进行查证,假如查证的对象是平民,他会告诉警察,他认识的人,谁是杀手,谁是平民。
假如查证的对象是杀手,杀手将会把警察干掉。
现在警察掌握了每一个人认识谁。
每一个人都有可能是杀手,可看作他们是杀手的概率是相同的。
问:根据最优的情况,保证警察自身安全并知道谁是杀手的概率最大是多少?
输入输出格式
输入格式:
第一行有两个整数 N,M。 接下来有 M 行,每行两个整数 x,y表示 x 认识 y(y 不一定认识 x ,例如President同志)。
注:原文zz敏感内容已替换
输出格式:
仅包含一行一个实数,保留小数点后面 6 位,表示最大概率。
输入输出样例
输入样例#1:
5 4
1 2
1 3
1 4
1 5
输出样例#1:
0.800000
说明
警察只需要查证1。假如1是杀手,警察就会被杀。假如1不是杀手,他会告诉警察2,3,4,5谁是杀手。而1是杀手的概率是0.2,所以能知道谁是杀手但没被杀的概率是0.8。
对于%100的数据有1≤N≤100000,0≤M≤300000。
一句话题意:
其实题目讲的跟实际意思有些区别,所以这里我就多啰嗦啰嗦。
(也许是作者太蒟蒻了看不来了,QAQ~~)
其实就是问你最少删多少个点,就能确保谁是杀手。
最后输出删点个数/n。(差点就没看出来)
删一个点,就能知道所有它能到达的点的信息。
[假如查证的对象是平民,他会告诉警察,他直接或间接认识的人的信息]
(而不是只能知道与它相邻的点的信息)
思路:
所以是不是只要统计入度为0的强连通分量的个数?
然而这道题出(sang)的(xin)最(bing)好(kuang)的一点就在于此(坑~~~~)
(不知道有多少人被坑,而将其评为紫题难度)
实际上,这道题也不——容易(蒟蒻作者错了好几[一~~]次)
我们如果知道n-1人的信息,就不用继续问。
所以如果有一强连通分量入度为0,
所含点个数为1,
且选择其它入度为0的强连通分量能走遍它所能到达的所有结点,
最后答案减1。
注意:如果有多个这样的点,只算一个。
代码:
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=1e5+6,M=3e5+6; 5 int n,m,cnt=0,head[N],head2[N],t1,t2,top=0,deep=0,tot=0; 6 int dfn[N],low[N],num[N],siz[N],s[N],rd[N],flag=0; 7 struct edge 8 { 9 int nxt,to; 10 }e[M],f[M]; 11 inline int read() 12 { 13 int T=0,F=1; char ch=getchar(); 14 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 15 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 16 return F*T; 17 } 18 inline void add1(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 19 inline void add2(int u,int v){f[++cnt].nxt=head2[u]; f[cnt].to=v; head2[u]=cnt; ++rd[v];} 20 void tarjan(int u) 21 { 22 dfn[u]=low[u]=++deep; s[++top]=u; 23 for(int i=head[u];i;i=e[i].nxt) 24 { 25 if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]); 26 else if(!num[e[i].to]) low[u]=min(low[u],dfn[e[i].to]); 27 } 28 if(low[u]==dfn[u]) 29 { 30 ++tot; siz[tot]=1; num[u]=tot; 31 while(s[top]!=u) ++siz[tot],num[s[top]]=tot,--top; 32 --top; 33 } 34 } 35 void dfs(int u) 36 { 37 dfn[u]=1; 38 for(int i=head2[u];i;i=f[i].nxt) 39 { 40 if(!dfn[f[i].to]) dfs(f[i].to); 41 ++low[f[i].to]; 42 } 43 } 44 int main() 45 { 46 n=read(),m=read(); 47 for(re int i=1;i<=m;++i) t1=read(),t2=read(),add1(t1,t2); cnt=0; 48 for(re int i=1;i<=n;++i) if(!dfn[i]) deep=top=0,tarjan(i); 49 for(re int i=1;i<=n;++i) for(int j=head[i];j;j=e[j].nxt) if(num[i]!=num[e[j].to]) add2(num[i],num[e[j].to]); 50 memset(dfn,0,sizeof(dfn)); memset(low,0,sizeof(low)); cnt=0; 51 //作者习惯了省吃俭用,能省则省,dfn和low就重复利用了。 52 //dfn代表走没走过,low代表走过几次 53 for(int i=1;i<=tot;++i) if(!dfn[i]) dfs(i); 54 for(int i=1;i<=tot;++i) 55 if(!rd[i]){ 56 if(siz[i]==1) 57 { 58 flag=1; 59 for(int j=head2[i];j;j=f[j].nxt) 60 if(low[f[j].to]==1) flag=0;//至少有一个点不能被其它点走到 61 } 62 ++cnt; 63 } 64 if(flag) --cnt; 65 printf("%.6lf\n",(double)((n-cnt)*1.0000000000/n)); 66 return 0; 67 }

