点双连通分量和边双连通分量学习笔记

点双连通分量和边双连通分量学习笔记

1.简介：

对于一个连通图，如果任意两点至少存在两条点不重复路径，则称这个图为点双连通的（简称双连通）；如果任意两点至少存在两条边不重复路径，则称该图为边双连通的。点双连通图的定义等价于任意两条边都同在一个简单环中，而边双连通图的定义等价于任意一条边至少在一个简单环中。对一个无向图，点双连通的极大子图称为点双连通分量（简称双连通分量），边双连通的极大子图称为边双连通分量。

而在每一个点双连通图中，内部无割点；

在每一个边双连通图中，内部无桥。

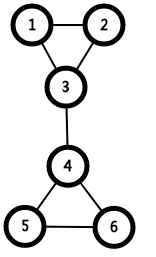
如图：

 

 

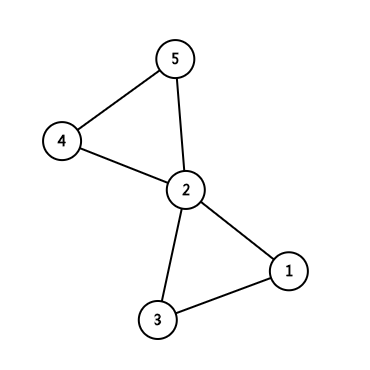
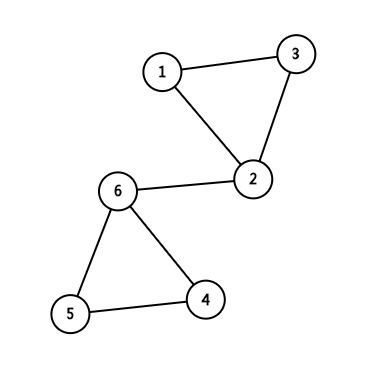
1、2、3，2、4、5为两个点双连通分量，1、2、3、4、5却在一个边双连通分量中；其中，2为割点。

而第二个图中，2-6边为桥。

 

2.性质：
  <1>.点双连通分量:
     (1).点双连通分量之间以割点连接，且两个点双连通分量之间有且只有一个割点。
         证明：
            若两个点双连通分量之间共用两个点，则删除其中任意一个点，所有点依旧连通。
         如图：

                        

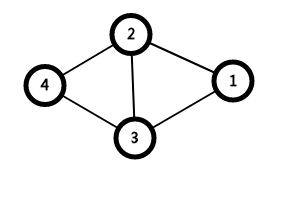
     (2).每一个割点可任意属于多个点双连通分量，因此求点双连通分量时，可能包含重复的点。
             (3).只有一条边连通的两个点也是一个点双连通分量，如：

        

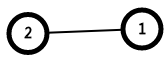
         所以，在下图中，存在（1、2、3）,（3、4），（4、5、6）三个点双连通分量。

         

     (4).对于此点为根的情况，第一个儿子也属于点双连通分量，故不能用判断割点的方法来判断，

         只要dfn[父]<=low[子]，便可将其加入点双：

        

 

                在此图中，1、2、3、4在同一个点双连通分量里，但2是1的第一个儿子

    (5).对于删去此点不会不与祖辈连通的儿子，在处理其他儿子的点双连通分量时，不能将其删去，如。

        

 

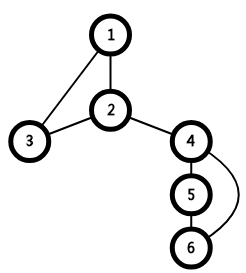
                    1、2、3共同构成一个点双连通分量，不能在处理4、5、6是将其删去。

                    所以代码不该为：

                    

         while(s[top]!=u) ++siz[tot]=s[top],num[s[top]]=tot,--top;

                   而应是

                   

        v=e[i].to;
        while(s[top+1]!=v) ++siz[tot],num[s[top]]=tot,--top;

       <2>.边双连通分量：

        可将图看作森林，节点为边双连通分量，树边为桥:

               

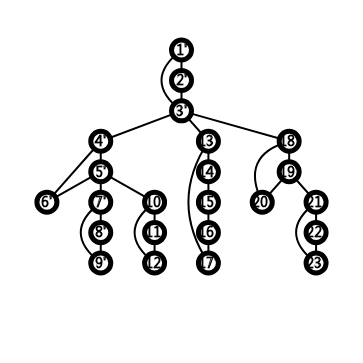
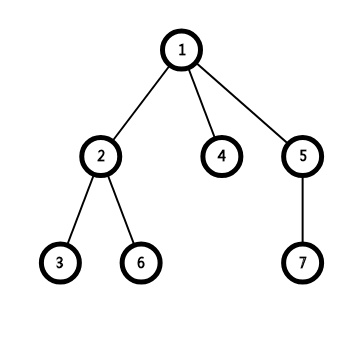
        第二张图是第一张图中的点双连通分量缩点后的样子。

 

     边双连通分量没有什么性质，反正也很简单。                   ——LY巨佬

3.做法和代码:

    日复一日的神仙tarjan算法：

     1>.点双连通分量：

        用栈来储存，按dfs序来加点，将此点与low小于其dfn的点放入一个点双连通分量中（注：此点不退栈）

        

void tarjan(int u)
{
    dfn[u]=low[u]=++deep; s[++top]=u; int o=0,v;
    for(int i=head[u];i;i=e[i].nxt)
    {
        v=e[i].to;
        if(!dfn[v])
        {
            ++o;
            tarjan(v),low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
            {
                if(u!=fa) cut[u]=1; ++tot;
                while(s[top+1]!=v) num[tot][++siz[tot]]=s[top],id[s[top]]=tot,--top;
                num[tot][++siz[tot]]=u;//将id[u]默认属于它父亲的tot了
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
    if(u==fa&&o>=2) cut[u]=1;
}

 

     2>.边双连通分量：

        删去桥就行了。

 

#include<bits/stdc++.h>
using namespace std;
const int N=5006,M=10006;
int head[N],cnt=1,n,m,t1,t2,book[N],dfn[N],low[N],deep=0,v[M*2],f[N],tot=0,d[N],g[N],p=0,num[N][N],siz[N];
map<int,int> ha[N];
int getf(int u){return g[u]==u?u:g[u]=getf(g[u]);}
void merge(int u,int v)
{
    u=getf(u); v=getf(v);
    if(u==v) return;
    g[u]=v;
}
struct edge
{
    int nxt,to;
}e[M*2]; 
inline int read()
{
    int T=0,F=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
    while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
    return F*T;
}
inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 
void tarjan(int u)
{
    dfn[u]=low[u]=++deep;
    for(int i=head[u];i;i=e[i].nxt)
    {
        if(v[i^1]||v[i]) continue;
        if(!dfn[e[i].to]) v[i]=1,f[e[i].to]=u,tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]);
        else low[u]=min(low[u],dfn[e[i].to]);
    }
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;++i) g[i]=i;
    for(int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2),add(t2,t1);
    for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
    for(int i=1;i<=n;++i) if(f[i]&&low[i]>dfn[f[i]]) ++tot,ha[i][f[i]]=1,ha[f[i]][i]=1;
    for(int i=1;i<=n;++i)
        for(int j=head[i];j;j=e[j].nxt) if(ha[i].find(e[j].to)==ha[i].end()) merge(i,e[j].to);
    for(int i=1;i<=n;++i) g[i]=getf(i);
    for(int i=1;i<=n;++i)
    {
        if(!book[g[i]]) ++p,d[g[i]]=p,book[g[i]]=1;
        g[i]=d[g[i]],num[g[i]][++siz[g[i]]]=i;
    } 
    printf("共有%d个边双连通分量\n",p);
    for(int i=1;i<=p;++i)
    {
        printf("第%d个边双连通分量共有%d个点",i,siz[i]);
        for(int j=1;j<=siz[i];++j) printf("%d ",num[i][j]);
        printf("\n");
    }
    return 0;
}