割点和桥学习笔记
割点和桥
1.什么是割点和桥:
如果在图G中去掉一个顶点(自然同时去掉与该顶点相关联的所有边)后,该图的连通分支数增加,则称该顶点为G的割点(割顶)(cut-vertex)。
设无向图G=<V,E>,若存在E'⊆E使得p(G-E')>p(G),且对于任意的E''⊂E',均有p(G-E'')=p(G),则称E'是G的边割集,或简称为割集。若E'={e},则称e为割边或桥。
--度娘
对于一个连通图,如果任意两点至少存在两条点不重复路径,则称这个图为点双连通的(简称双连通);如果任意两点至少存在两条边不重复路径,则称该图为边双连通的。点双连通图的定义等价于任意两条边都同在一个简单环中,而边双连通图的定义等价于任意一条边至少在一个简单环中。对一个无向图,点双连通的极大子图称为点双连通分量(简称双连通分量),边双连通的极大子图称为边双连通分量。
而在每一个点双连通图中,内部无割点;
在每一个边双连通图中,内部无桥。
如图:
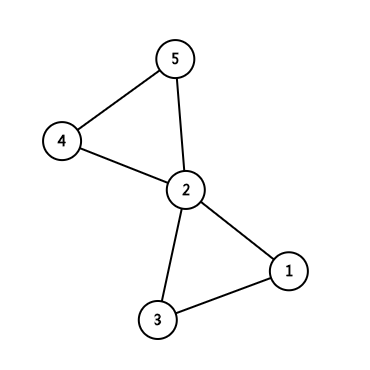
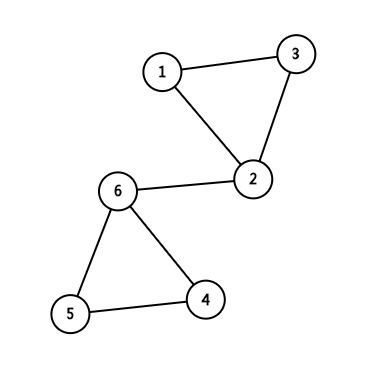
1、2、3,2、4、5为两个点双连通分量,1、2、3、4、5却在一个边双连通分量中;其中,2为割点。
而第二个图中,2-6边为桥。
2.怎么判断割点和桥:
Tarjan算法,老朋友了。
对于每个点,我们dfs求出dfs序,设这个点为u,其儿子为v;
若所有v不能到达dfs序小于u的点,则删去u所有v不与和dfs序小于u的点连通,连通块个数增加,所以u为割点;
当然,还有错误!!!
对于第一个搜索的点(dfs序为1)来说,若只有一个子节点,便不是割点!
如:

若v除了u-v边,不能到达dfs序小于等于u的点,u-v便是桥。
上图中,3没有其它边到2,所以2-3为桥;而4的父亲是3,还可以通过4-5,5-3到3,不是桥。
下面论证tarjan算法的正确性:
1.为什么可以搜到所有桥:
桥最多有n-1条,
因为对于一个点来说,最多向父节点连一条桥,而如果超过一条,父子间就不存在桥;
而向儿子们连的桥,可将其视作属于儿子们。
2.为什么可以搜到所有割点:
将这个点的祖宗看作一个连通块,将它的每个儿子看作一个连通块,它是连接多个连通块的关键点,
如果删去它之后,所有儿子连通块跟祖宗连通块相连,此点不是割点;
只要有一个子连通块不跟父连通块相连通,删去它后连通块个数增加,是割点。
你可能会想问:可不可能存在删去它后,几个子连通块与父连通块连通,其它子连通块与这几个子连通块连通呢?
不存在的!
根据dfs的性质,除了父亲,其它与它连通的都是儿子。
如果“其它子连通块与这几个子连通块连通”,“其它子连通块”原来就属于“这几个子连通块”。
最后贴贴代码:
割点:
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=20006,M=200006; 5 int n,m,low[N],head[N],dfn[N],deep=0,cnt=0,is_cut[N],t1,t2,tot=0; 6 struct edge 7 { 8 int nxt,to; 9 }e[M]; 10 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 11 inline int read() 12 { 13 int T=0,F=1; char ch=getchar(); 14 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 15 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 16 return F*T; 17 } 18 void tarjan(int u,int fa) 19 { 20 dfn[u]=low[u]=++deep; int num=0,v; 21 for(int i=head[u];i;i=e[i].nxt) 22 { 23 v=e[i].to; 24 if(!dfn[v]) 25 { 26 ++num,tarjan(v,u),low[u]=min(low[u],low[v]); 27 if(fa&&low[v]>=dfn[u]) is_cut[u]=1; 28 } 29 else low[u]=min(low[u],dfn[v]); 30 } 31 if(!fa&&num>=2) is_cut[u]=1; 32 } 33 int main() 34 { 35 n=read(); m=read(); 36 for(re int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2),add(t2,t1); 37 for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0); 38 for(int i=1;i<=n;++i) if(is_cut[i]) ++tot; 39 printf("%d\n",tot); 40 for(int i=1;i<=n;++i) if(is_cut[i]) printf("%d ",i); 41 return 0; 42 }
桥:
1 #include<bits/stdc++.h> 2 #define re register 3 using namespace std; 4 const int N=20006,M=200006; 5 int n,m,low[N],head[N],dfn[N],deep=0,cnt=0,t1,t2,f[N]; 6 struct edge 7 { 8 int nxt,to; 9 }e[M]; 10 inline void add(int u,int v){e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt;} 11 inline int read() 12 { 13 int T=0,F=1; char ch=getchar(); 14 while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();} 15 while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar(); 16 return F*T; 17 } 18 void tarjan(int u,int fa) 19 { 20 f[u]=fa; dfn[u]=low[u]=++deep; int v; 21 for(int i=head[u];i;i=e[i].nxt) 22 { 23 v=e[i].to; 24 if(!dfn[v]) tarjan(v,u),low[u]=min(low[u],low[v]); 25 else if(v!=fa) low[u]=min(low[u],dfn[v]); 26 } 27 } 28 int main() 29 { 30 n=read(); m=read(); 31 for(re int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2),add(t2,t1); 32 for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0); 33 for(int i=1;i<=n;++i) 34 if(f[i]&&low[i]>dfn[f[i]]) printf("%d %d\n",i,f[i]); 35 return 0; 36 }


