缩点(有向图的强连通分量)学习笔记

缩点(有向图的强连通分量)学习笔记

1.什么是强连通分量？：

有向图强连通分量:在有向图G中，如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。——度娘

显然正确，但是文绉绉的又难懂。

其实就是有一大团点，它们之间可以互相到达，且没有其它的点与它们互可到达，那么这一大团点就是有向图的一个强联通分量。

一个强连通分量可以看作一个或几个环拼接在一起。

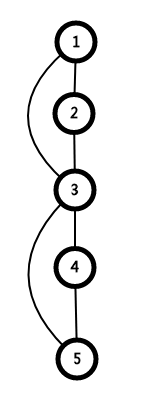
如：

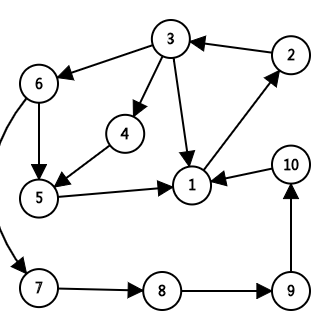
2.如何操作？：

首先对于整个有向图进行dfs，若dfs树中存在子树有到达父亲节点，从父亲到这个点则都可互相到达，这些点有可能与父亲原属的强连通图合并,也有可能成为新的一个强连通分量。

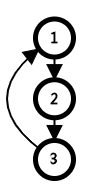
如上图。

所以我们判断一个点是否在一个强连通分量中，就用它是否能到达dfs序比他小的点。

但我们如何将一个强连通分量的点记录呢？

答：用一个栈储存，遇到一个不能到达dfs序比他小的点的点，就将栈里的点都标记为一个新的强连通分量，再清空栈（一个点我们也看作一个强连通分量）。

我们用dfn数组记录dfs序，low数组记录能到达的点最小的dfs编号。

对于每一个点，需要用它的儿子的low来更新自己的low,如上图中的2号点;

然而，若有连向父亲的边呢？是不是直接用父亲的dfn来更新自己的low？

当然是对的！！！（作者就曾经错在这里,曾今以为是对的，但打模板时错了，改了两处，结果以为是因为将dfn改为low才对的，后面发现不是，果然我还是太蒟蒻了qaq_~~~~~）

在tarjan算法中，都是用父亲的dfn来更新自己的low,

但在有向图中，若自己的父亲有连向祖父等祖宗，那么自己和祖宗在同一个强连通分量；

而在无向图中，则属于两个强连通分量。

如：

                                 

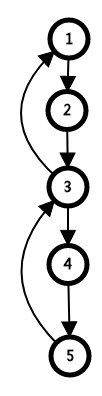
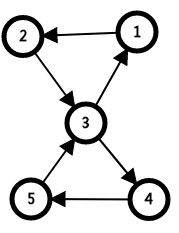
其中，1、2、3、4、5互可到达，只有dfn[1]==low[1]，都是一个强连通分量。

           

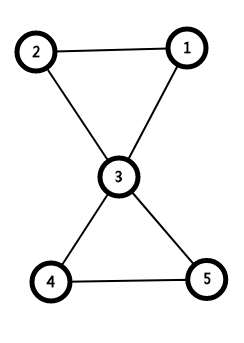
此时，用low来更新错误

 

还有，注意：对于已经属于一个强连通分量的点，不能用它的low来更新连向它的点！

       

所以，low[5]为5。

 

void tarjan(int u)//当前点
{
    low[u]=dfn[u]=++deep; x[++top]=u; v[u]=1;
    for(int i=head1[u];i;i=e[i].nxt)
    {
        if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]);//连向儿子的边
        else if(v[e[i].to]) low[u]=min(low[u],low[e[i].to]);//连向父亲且不属于一个强连通分量
    }
   if(dfn[u]==low[u])//找到一个强连通分量
   {
        num[u]=++tot; v[u]=0;
        while(x[top]!=u) v[x[top]]=0,num[x[top]]=tot,--top;
        --top;
     }
}
int main()
{
    for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
    return 0;
}

 

 

 

最后，模拟一个图的tarjan过程：

 

一共有一个强连通分量:1.{1,2,3,4,5,6,7,8,9}。

u=1:dfn[1]=1,++top,x[1]=1,tarjan(8);

u=8:dfn[8]=2,++top,x[2]=8,tarjan(9);

u=9:dfn[9]=3,++top,x[3]=9,low[9]=1;

u=8:low[8]=1;

u=1:tarjan(2);

u=2:dfn[2]=4,++top,x[4]=2,tarjan(3);

u=3:dfn[3]=5,++top,x[5]=3,tarjan(4);

u=4:dfn[4]=6,++top,x[6]=4,low[4]=low[2]=4;

u=3:low[3]=low[4]=4;

u=2:low[2]=4,tarjan(5);

u=5:dfn[5]=7,++top,x[7]=5,tarjan(6);

u=6:dfn[6]=8,++top,x[8]=6,tarjan(7);

u=7:dfn[7]=9,++top,x[9]=7,low[7]=1;

u=6:low[6]=1;

u=5:low[5]=1;

u=2:low[2]=1;

u=1:dfn[1]==low[1]=1→++tot,将x[1]到x[9]标记为tot=1,top=0;

结束。

3.缩点：

将每个强联通分量看作一点，将所有连向强联通分量内的点连向这个强联通分量。

int main()
{
    n=read(); m=read();
    for(int i=1;i<=n;++i) w1[i]=read();
    for(re int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2,e,head1);
    cnt=0;
    for(int i=1;i<=n;++i)
    {
        w2[num[i]]+=w1[i];
        for(int j=head1[i];j;j=e[j].nxt) if(num[i]!=num[e[j].to]) add(num[i],num[e[j].to],f,head2),++rd[num[e[j].to]];
    }
    return 0;
}

洛谷P3387 【模板】缩点

题目背景

缩点+DP

题目描述

给定一个n个点m条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

输入输出格式

输入格式：

 

第一行，n,m

第二行，n个整数，依次代表点权

第三至m+2行，每行两个整数u,v，表示u->v有一条有向边

 

输出格式：

 

共一行，最大的点权之和。

 

输入输出样例

输入样例#1： 

2 2
1 1
1 2
2 1

输出样例#1： 

2

说明

n<=10^4,m<=10^5,0<=点权<=1000

算法：Tarjan缩点+DAGdp

题解:

当进入一个强连通分量时，肯定将这个强连通分量都走一遍，所以缩点，变为一个DAG（有向无环图），然后按拓扑序dp，每个点的答案为所有能到达它的点的答案的最大值+自己的点值，输出所有点中答案的最大值。

用每个点的答案更新它所能到达的所有点的答案。

代码如下：

#include<bits/stdc++.h>
#define re register
using namespace std;
const int N=10006,M=100006;
int n,m,t1,t2,w1[N],w2[N],num[N],cnt=0,head1[N],t,tot=0,head2[N],x[N],dfn[N],low[N],ans[N],maxa=-1,rd[N],deep=0,top=0,v[N];
struct edge
{
    int to,nxt;
}e[M],f[M];
inline void add(int u,int v,edge a[],int head[]){a[++cnt].to=v,a[cnt].nxt=head[u],head[u]=cnt;}
inline int read()
{
    int T=0,F=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
    while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
    return F*T;
}
void tarjan(int u)
{
    low[u]=dfn[u]=++deep; x[++top]=u; v[u]=1;
    for(int i=head1[u];i;i=e[i].nxt)
    {
        if(!dfn[e[i].to]) tarjan(e[i].to),low[u]=min(low[u],low[e[i].to]);
        else if(v[e[i].to]) low[u]=min(low[u],low[e[i].to]);
    }
    if(dfn[u]==low[u])
    {
        num[u]=++tot; v[u]=0;
        while(x[top]!=u) v[x[top]]=0,num[x[top]]=tot,--top;
        --top;
    }
}
void tppx()
{
    queue<int> q; cnt=0;
    for(int i=1;i<=tot;++i) if(!rd[i]) x[++cnt]=i,q.push(i);
    while(!q.empty())
    {
        int tmp=q.front(); q.pop();
        for(int i=head2[tmp];i;i=f[i].nxt)
        {
            --rd[f[i].to];
            if(!rd[f[i].to]) x[++cnt]=f[i].to,q.push(f[i].to);
        }
    }
}
int main()
{
    n=read(); m=read();
    for(int i=1;i<=n;++i) w1[i]=read();
    for(re int i=1;i<=m;++i) t1=read(),t2=read(),add(t1,t2,e,head1);
    for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
    cnt=0;
    for(int i=1;i<=n;++i)
    {
        w2[num[i]]+=w1[i];
        for(int j=head1[i];j;j=e[j].nxt) if(num[i]!=num[e[j].to]) add(num[i],num[e[j].to],f,head2),++rd[num[e[j].to]];
    }
    memset(x,0,sizeof(x)); tppx();
    for(int i=1;i<=n;++i)
    {
        t=x[i]; ans[t]=max(ans[t],w2[t]);
        maxa=max(maxa,ans[t]);
        for(int j=head2[t];j;j=f[j].nxt) ans[f[j].to]=max(ans[f[j].to],ans[t]+w2[f[j].to]);
    }
    printf("%d\n",maxa);
    return 0;
}