数据分析第四篇：相关分析

相关分析是数据分析的一个基本方法，可以用于发现不同变量之间的关联性，关联是指数据之间变化的相似性，这可以通过相关系数来描述。发现相关性可以帮助你预测未来，而发现因果关系意味着你可以改变世界。

一，协方差和相关系数

如果随机变量X和Y是相互独立的，那么协方差

Cov(X,Y) = E{ [X-E(X)] [Y-E(Y)] } = 0，

这意味着当协方差Cov(X,Y) 不等于 0 时，X和Y不相互独立，而是存在一定的关系，此时，称作X和Y相关。在统计学上，使用协方差和相关系数来描述随机变量X和Y的相关性：

协方差：如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。从数值来看，协方差的数值越大，两个变量同向程度也就越大。

，µ是变量的期望。

相关系数：相关系数消除了两个变量变化幅度的影响，只是单纯反应两个变量每单位变化时的相似程度。

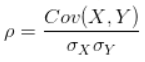，δ是变量的标准差。

相关系数用于描述定量变量之间的关系，相关系数的符号（+、-）表明关系的方向（正相关、负相关），其值的大小表示关系的强弱程度（完全不相关时为0，完全相关时为1）。

例如，下面两种情况中，很容易看出X和Y都是同向变化的，而这个“同向变化”有个非常显著特征：X、Y同向变化的过程，具有极高的相似度。

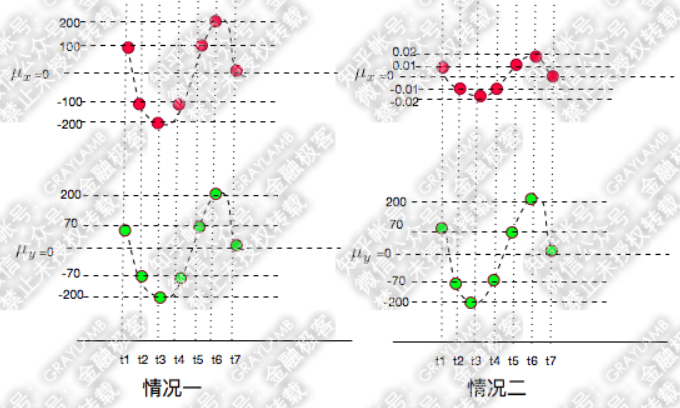
1，观察协方差，情况一的协方差是：

情况二的协方差是：

协方差的数值相差一万倍，只能从两个协方差都是正数判断出在这两种情况下X、Y都是同向变化，但是一点也看不出两种情况下X、Y的变化都具有相似性这一特点。

2，观察相关系数，情况一的相关系数是：

情况二的相关系数是：

虽然两种情况的协方差相差1万倍，但是，它们的相关系数是相同的，这说明，X的变化与Y的变化具有很高的相似度。

二，相关的类型

R可以计算多种相关系数，包括Pearson相关系数、Spearman（秩）相关系数、Kendall（秩）相关系数、偏相关系数等相关系数，相关系数描述的是变量之间的线性相关程度。

Pearson相关系数衡量了两个连续型变量之间的线性相关程度，要求数据连续变量的取值服从正态分布；
Spearman等级相关系数衡量两个变量之间秩次（排序的位置）的相关程度，通常用于计算离散型数据、分类变量或等级变量之间的相关性；
Kendall等级相关系数用于计算有序的分类变量之间的相关系数，对于有序的分类变量，例如，评委对选手的评级，优、中、差等。

1，R函数

cor()函数可以计算相关系数，而cov()函数用于计算协方差：

cor(x, y = NULL, use = "everything", method = c("pearson", "kendall", "spearman"))
cov(x, y = NULL, use = "everything", method = c("pearson", "kendall", "spearman"))

参数注释：

x：矩阵或数据框
y：默认情况下，y=NULL表示y=x，也就是说，所有变量之间两两计算相关，也可以指定其他的矩阵或数据框，使得x和y的变量之间两两计算相关。
use：指定缺失数据的处理方式，可选的方式为all.obs（遇到缺失数据时报错）、everything（遇到缺失数据时，把相关系数的计算结果设置为missing）、complete.obs（行删除）以及pairwise.complete.obs（成对删除）
method：指定相关系数的类型，可选类型为"pearson", "kendall", "spearman"

例如，使用R基础安装包中的state.x77数据集，它提供了美国50个州的人口、收入、文盲率（Illiteracy）、预期寿命（Life Exp）、谋杀率和高中毕业率（HS Grad）等数据。

states <- state.x77[,1:6]

> cor(states)
            Population     Income Illiteracy    Life Exp     Murder     HS Grad
Population  1.00000000  0.2082276  0.1076224 -0.06805195  0.3436428 -0.09848975
Income      0.20822756  1.0000000 -0.4370752  0.34025534 -0.2300776  0.61993232
Illiteracy  0.10762237 -0.4370752  1.0000000 -0.58847793  0.7029752 -0.65718861
Life Exp   -0.06805195  0.3402553 -0.5884779  1.00000000 -0.7808458  0.58221620
Murder      0.34364275 -0.2300776  0.7029752 -0.78084575  1.0000000 -0.48797102
HS Grad    -0.09848975  0.6199323 -0.6571886  0.58221620 -0.4879710  1.00000000

可以看到，收入和高中毕业率之间存在很强的正相关（约0.620），文盲率和谋杀率之间存在很强的正相关（约0.703），文盲率和高中毕业率之间存在很强的负相关（约-0.657），预期寿命和谋杀率之间存在很强的负相关（约-0.781）等。

2，Pearson相关系数

Pearson线性相关系数一般用于分析连个连续性变量之间的线性相关的程度，计算公式是：

Pearson线性相关系数要求连续变量的取值服从正太分布，相关系数r的取值范围是： -1 <= r <= 1，相关系数有如下特征：

r>0 表示正相关，r<0表示负相关；
r=0 表示不存在线性关系
r=1 或 r=-1 表示存在完全的线性关系

0 < | r | <1表示变量之间存在不同程度的线性相关，根据约定的规则：

| r | <=0.3 ：为弱线性相关或不存在线性相关；
0.3 < | r | <=0.5 ：低度线性相关，认为存在线性相关，但是相关性不明显
0.5 < | r | <=0.8 ：显著线性相关，认为存在强线性相关，存在明显的相关性
| r | >0.8 ：高度相关，认为存在极强的线性相关

3，Spearman秩相关系数

对于分类或等级变量之间的关联性，可以采用Spearman秩相关系数（也称作等级相关系数）来描述。“秩”是一种顺序或者排序，秩相关系数是根据原始数据的排序位置进行求解，计算公式如下，d是秩次差的平方，n是等级个数：

秩次是指数据排序之后的序号，对于有序的分类序列，1、3、5、6、8，数值1的秩次是1，数字5的秩次是3。对于同一个变量，相同的取值必须具有相同的秩次，例如：

例如，按照从大到小的顺序对X和Y进行排序：

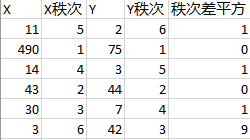
Spearman秩相关系数其实是利用两变量的秩次大小作线性相关分析，下表用于计算变量X和Y的秩相关系数 ρ = 1 - 6*(1+1+1+9) / (6*35) =0.657

从Spearman秩相关系数的计算过程中，可以看到，不管X和Y这两个变量的值差距有多大，只需要算一下它们每个值所处的排列位置的差值，就可以求出秩相关性系数。

4，Kendall等级相关系数

Kendall等级（Rank）相关系数，是一种秩相关系数，kendall秩相关系数用于：有n个统计对象，每个对象有两个属性，检查这两个属性的变化是否一致。

举个例子，假设老师对评委的评价等级：3表示优、2表示中、1表示差，使用评分的Kendall相关系数，查看2位评委对6位选手的评价标准是否一致：

X <- c(3,1,2,2,1,3)
Y <- c(1,2,3,2,1,1)
cor(X,Y,method="kendall")
[1] -0.2611165

再举个例子，有一组8人的身高和体重，先按照身高排序，再按照体重排序，我们得到两组数据：

使用Kendall等级相关系数这两个排名（按身高排名和按体重排名）之间的相关性。

5，偏相关

偏相关是指在控制一个或多个定量变量（称作条件变量）时，另外两个定量变量之间的相关关系。可以使用ggm包中的pcor()函数计算偏相关系数。

pcor(u, S)

参数注释：

u：位置向量，前两个整数表示要计算偏相关系数的变量下标，其余的整数为条件变量的下标。
S：是数据集的协方差矩阵，即cov()函数计算的结果

例如：在控制了收入、文盲率和高中毕业率的条件下，计算的人口和谋杀率之间的偏相关系数为0.346：

> library(igraph)
> library(ggm)
> colnames(states)
[1] "Population" "Income"     "Illiteracy" "Life Exp"   "Murder"     "HS Grad"  
> pcor(c(1,5,2,3,6),cov(states))
[1] 0.3462724

三，相关性的显著性检验

在计算好相关系数之后，需要对相关性进行显著性检验，常用的原假设是变量间不相关（即总体的相关系数为0），可以使用cor.test()函数对单个的Pearson、Spearman和Kendall相关系数进行显著性检验，以验证原假设是否成立。如果p值很小，说明变量之间存在相关性，相关性的大小由相关系数确定。

显著性检验返回的结果中，p值（p value）就是当原假设为真时所得到的样本观察结果出现的概率。如果p值很小，说明原假设情况的发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，p值越小，我们拒绝原假设的理由越充分。

小概率原理是指：在统计学中，通常把在现实世界中发生几率小于5%的事件称之为“不可能事件”，通常把显著性水平定义为0.05，或0.025。当p值小于显著性水平时，把原假设视为不可能事件，因为拒绝原假设。

1，cor.test()检验

cor.test()每次只能检验一种相关关系，原假设是变量间不相关，即总体的相关系数是0。

cor.test(x, y,
         alternative = c("two.sided", "less", "greater"),
         method = c("pearson", "kendall", "spearman"),
         exact = NULL, conf.level = 0.95, continuity = FALSE, ...)

参数注释:

alternative：用于指定进行双侧检验还是单侧检验，有效值是 "two.sided", "greater" 和 "less"，对于单侧检验，当总体的相关系数小于0时，使用alternative="less"；当总体的相关系数大于0时，使用alternative="greater"；默认情况下，alternative="two.side"，表示总体相关系数不等于0。
method：指定计算的相关类型，
exact：逻辑值，是否计算出精确的p值
conf.level：检验的置信水平

例如，下面的代码用于检验预期寿命和谋杀率的Pearson相关系数为0的原假设，

> cor.test(states[,3],states[,5])

    Pearson's product-moment correlation

data:  states[, 3] and states[, 5]
t = 6.8479, df = 48, p-value = 1.258e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.5279280 0.8207295
sample estimates:
      cor 
0.7029752

检验的结果是：p值（p-value=1.258e-08)，样本估计的相关系数cor 是 0.703，这说明：

假设总体的相关度为0，则预计在1千万次中只会有少于1次的机会见到0.703的样本相关度，由于这种情况几乎不可能发生，所以拒绝原假设，即预期寿命和谋杀率之间的总体相关度不为0。

2，corr.test()检验

psych包中的corr.test()函数，可以依次为Pearson、Spearman或Kendall计算相关矩阵和显著性水平。

corr.test(x, y = NULL, use = "pairwise",method="pearson",adjust="holm", alpha=.05,ci=TRUE)

参数注释：

use：指定缺失数据的处理方式，默认值是pairwise（成对删除）；complete（行删除）
method：计算相关的方法，Pearson（默认值）、Spearman或Kendall

3，偏相关的显著性检验

在多元正态性的假设下，psych包中的pcor.test()函数用于检验在控制一个或多个条件变量时，两个变量之间的独立性。

pcor.test(r, q, n)

参数注释：

r：是由pcor()函数计算得到的偏相关系数
q：要控制的变量（以位置向量表示）
n：样本大小

四，相关图

利用corrgram包中的corrgram()函数，使用图形来显示相关系数矩阵，

corrgram(x, order = FALSE,lower.panel = panel, upper.panel = panel, text.panel = textPanel, main='title'
  col.regions = colorRampPalette(c("red", "salmon","white", "royalblue", "navy")), cor.method = "pearson",...)

常用的参数注释：

x：数据集
order：变量是否被排序
lower.panel / upeer.panel：对角线下/上的面板
text.panel=panel.txt：对角线显示为文本
main：主标题
col.regions：颜色，使用该参数控制函数中使用的颜色。
cor.method：做相关分析的函数名称，默认值是person，其他可用的值是：spearman, kendall

例如，以mtcars数据框中的变量相关性为例，它含有11个变量，对每个变量都测量了32辆汽车，使用corrgram()函数获得相关系数：

> library(corrgram)
> corrgram(mtcars,order = TRUE, lower.panel = panel.ellipse,upper.panel = panel.pie,text.panel = panel.txt,main='Corrgram of mtcars intercorrelations')

对于相关图矩阵，对角线上显示的是变量的名称，该变量实际上是垂直的直线和水平的直线的交点，这两条直线上的各个点表示也是该变量。