统计1:概述
概率论是人们在长期实践中发现的理论,是客观存在的。自然界和社会上发生的现象是多种多样的,有一类现象,在一定条件下必然发生,称作确定性现象,而概率论研究的现象是不确定性现象,嗯嗯,醒醒,概率论研究的对象是随机现象。那什么是随机现象呢?在个别试验中呈现出不确定性,而在大量重复实验中呈现出固有规律性的现象,称作随机现象,在大量重复实验中所呈现的固有规律,是统计规律性,也就是概率。
一,概率和频率
在提到概率之前,不得不说频率。对于一个随机事件来说,在一次试验中可能发生,也可能不发生,那么,如何表征事件在一次试验中发生的可能性大小呢?为了解答这个问题,引入了频率。频率描述了事件发生的频繁程度,频率越大,事件发生的越频繁,这意味着事件在一次试验中发生的可能性越大。我们定义,概率表征事件在一次试验中发生的可能性大小,因此,可从频率引出概率。
大数定理和中心极限定理是概率论的基本理论。大数定理论证了频率具有稳定性,中心极限定理表明了正态分布是普遍适用的。
概率是事件的固有规律,必须是稳定的一个数值,频率具有稳定性吗?在长期实践中,当试验次数不断增大时,事件发生的频率稳定在一个值附近,这一客观事实证明频率具有稳定性。伯努利大数定理用数学公式证明了频率的稳定性,因此,在实际应用中,当试验次数很大时,可以用事件的频率来代替事件的概率,用于表征事件发生的可能性大小。
正态分布是最重要的概率分布之一,中心极限定理表明,在相当一般的条件下,当独立随机变量的个数不断增加时,其和的分布趋于正太分布,通俗地说,如果一个事件受到N(N趋近于无穷)个独立因素的共同影响,且每个因素产生的影响都是独立的,那么这个事件发生的概率就服从中心极限定理,收敛于正态分布。因此,在实际应用中,正态分布是非常重要的,只要影响因素足够多,每个因素的作用都很微小,不必考虑每个因素服从什么分布,都可以用正态分布来预测事件发生的概率。
在研究概率论时,可以使用随机变量代表随机试验的一个结果,而这个随机变量具有数值属性,代表一个数值,这使得,可以使用数学分析的方法来描述随机现象。随机变量的取值随实验的结果而定,在试验之前不能预知事件的概率,且它的取值有一定的概率。在计算概率时,根据随机变量是否可以罗列,把随机变量分为离散型和连续型。
二,离散性随机变量
如果随机变量的全部取值是有限个或可列无限多个,这种随机变量称作离散性随机变量。 离散性随机变量使用分布规律来研究,服从二项分布或泊松分布。要归纳一个离散型随机变量的统计规律,只需要知道随机变量的可能取值,以及每一个取值的可能值。也就是说,对于每一个可能的取值,都有一个数值来表征该值出现的可能性。
1,二项分布
二项分布频繁地用于对以下描述的一种实验进行建模:从总数量大小为N的两个事物中进行n次放回抽样,以某一事物为基准,计算成功抽取这个事物的次数的概率。要注意的是必须进行的是放回抽样。
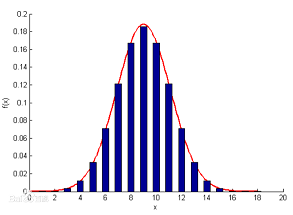
设随机变量X服从0-1分布,X只可能取0和1两个值,在n次实验中,X发生k次的概率是:
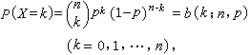
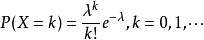
泊松分布的参数λ是单位时间内随机事件平均发生的次数。泊松分布的图形大概是
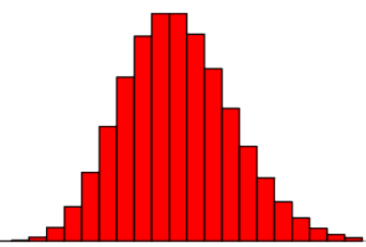
可以看到,泊松分布的特点是概率先随着k值的增加而增加,再达到顶点后,随着k值的增加而减少。
三,连续性随机变量
对于连续性随机变量,由于其可能的取值不能一一列举出来,通常情况下,连续性随机变量取某一个值的概率都是0。连续性随机变量使用概率密度来研究,服从概率密度函数。常用的概率密度是:均匀分布,指数分布和正态分布。 概率密度是什么意思?简单来说,就是连续随机变量落在某个区间的面积就是其概率。
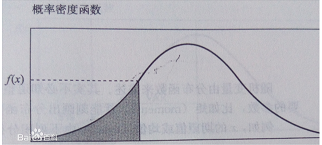
从坐标系上看,把概率密度看成是纵坐标,区间看成是横坐标,概率密度对区间的积分就是面积,而这个面积就是事件在这个区间发生的概率,所有区间的面积的和为1,因此,事件发生在某一个区间内的概率就是面积的大小。
1,指数分布
指数分布(也称为负指数分布)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程,因此,指数分布用来表示独立随机事件发生的时间间隔的概率分布:

其中,x是两个事件发生之间的时间间隔,λ > 0是指数分布的一个参数,常被称为率参数(rate parameter),即每单位时间内发生某事件的次数,指数分布的x区间是[0,∞)。 如果一个随机变量X呈指数分布,则可以写作:X~ E(λ)。
无记忆性是指数函数的一个重要特征,无记忆性(Memoryless Property)又称遗失记忆性,这表示如果一个随机变量呈指数分布,当s,t>0时,有P(T>t+s|T>t)=P(T>s),
如果T是某一元件的寿命,已知元件使用了t小时,它总共使用至少s+t小时的条件概率,与从开始使用时算起它使用至少s小时的概率相等,也就是说,元件对它已经使用过的s小时没有记忆。
指数分布的概率密度函数如下图所示:
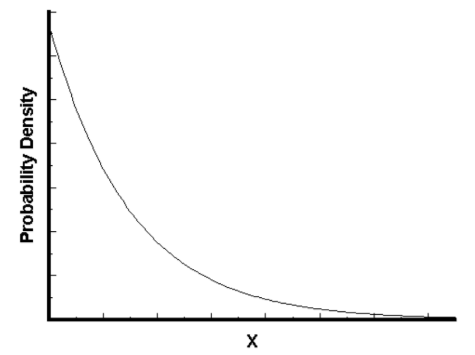
可以看到,随着间隔时间变长,事件发生的概率急剧下降,呈指数式衰减。

2,正态分布
正态分布的的概率密度函数是,其中μ,σ( σ>0)为常数,μ是数学期望,σ是标准差。
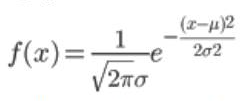
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为X~N(μ,σ2),其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。我们把μ = 0,σ = 1的正态分布是标准正态分布。
结论:若 X~N(μ,σ2),那么随机变量X的期望和方差是:E(X)=μ,D(X)=σ2。
正态分布的概率密度图形如下所示:
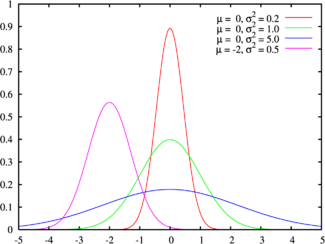
正态分布曲线的性质:
- 关于x=μ对称,并且当x=μ时,取得最大值。
- 固定μ,改变σ的值,由于最大值f(μ)跟σ 负相关,当σ越小,图形变得越尖,因为X落在μ附近的概率越大,σ被称作幅度参数。
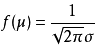
- 固定σ,改变的值μ,则图形沿着Ox轴平移,而不改变其形状,μ被称为位置参数。
四,随机变量的数字特征
对于单个随机变量,有两个描述性统计量:
- 数学期望,是随机变量的均值,是随机变量和概率的乘积的加和。
- 方差:表征随机变量和均值的偏离程度。
两个随机变量之间的线性关系:
- 协方差表征两个随机变量的变化相关程度。通俗地说,是两个变量在变化过程中是同方向变化(同时增大),还是反方向变化(一个增大,一个减小),以及变化的程度(数值越大,同向程度越大)。
- 相关系数,也称为线性相关系数,用于表征两个随机变量的线性变化的相关程度,如果相关系数是0,表示两个随机变量之间没有关系,不相关。
1,数学期望

2,方差
方差刻画了随机变量的取值对于其数学期望的离散程度。(标准差、方差越大,离散程度越大)

3,协方差
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。

4,相关系数
相关系数消除了两个变量变化幅度的影响,只是单纯反应两个变量每单位变化时的相似程度。

五,样本和抽样
数据统计是以概率论为理论基础,根据试验数据来研究随机现象,根据客观规律对研究对象做出合理的估计和推断。数理统计的内容包括:收集和整理资料、统计推断,而统计推断的基本问题是:估计问题和假设检验。
对某一项数量指标进行实验,进而预测该指标的数值,是数理统计研究的课题。对某一个指标,在试验中出现的所有可能的观察值称为总体,每一个可能的观察值称为个体,总体中所包含的个数称为总体的容量。在实际中,总体的分布是未知的,通过从总体中抽取一部分个体,根据样本数据对总体的分布做出推断,被抽取的部分个体叫做总体的一个样本。
一个总体对应一个随机变量X,对总体X进行一次观测记作随机变量X1,观测的结果记作x1。当进行n次观察后,得到一组实数x1, x2, ... , xn,它们依次是随机变量X1, X2, ..., Xn的观察值,称为样本值。
从总体中抽取一个个体,叫做一次抽样。为了逼近总体的分布,抽样时需要满足两个条件:
- 抽样的个体和总体具有相同的分布;
- 抽样的个体相互独立;
采用这种方式得到的样本,我们有理由近似地认为样本分布和总体分布相同,这样的样本称作简单随机样本。
抽样分为放回抽样和不放回抽样,对于有限总体,采用放回抽样就能得到简单随机样本,但是,返回抽样使用起来不方便,当个体的总数要比样本的容量大的多时,在实际中,通常把不放回抽样近似地当作返回抽样。
总结:总体的分布一般是未知的,在实际的统计推断中,都是利用样本的信息推断总体,得到有关总体分布的信息。
六,统计量
样本是进行统计推断的依据,定义 设X1, X2, ..., Xn是来自总体X的一个样本,g(X1, X2, ..., Xn)是样本X1, X2, ..., Xn的函数,若g中不含未知数,则称 g(X1, X2, ..., Xn) 是一个统计量。
统计量是随机变量的一个函数,是对样本的一个量化指标,常用的统计量是:
样本均值: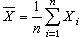
样本方差:
样本k阶矩,ak是原点距,mk是中心距:
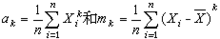
七,抽样分布
统计量的分布称为抽样分布,在使用统计量进行统计推断时,需要知道统计量的分布。当总体的分布函数已知时,抽样分布是确定的。
统计量也称作样本估计量,是样本的一个函数,以样本平均数为例,它是总体平均数的一个估计量,如果按照相同的样本容量,相同的抽样方式,反复地抽取样本,每次可以计算一个平均数,所有可能样本的平均数所形成的分布,就是样本平均数的抽样分布。
三大抽样分布是指卡方分布(χ2分布)、t分布和F分布,是来自正态总体的三个常用的分布。
八,显著性检验
在统计学中,显著性检验是“假设检验”中最常用的一种,显著性检验是用于检测科学实验中实验组与对照组之间是否有差异以及差异是否显著的办法。
显著性检验是假设检验的一种,那什么是假设检验?假设检验就是事先对总体(随机变量)的参数或总体分布形式做出一个假设,然后利用样本信息来判断这个假设是否合理。
在验证假设的过程中,总是提出两个相互对立的假设,把要检验的假设称作原假设,记作H0,把与H0对立的假设称作备择假设,记作H1。假设检验需要解决的问题是:指定一个合理的检验法则,利用已知样本的数据作出决策,是接受假设H0,还是拒绝假设H0。
什么是显著性检验?由于检验法则是根据样本作出的,总有可能做出错误的决策。在假设H0实际上为真时,做出拒绝H0的错误,称这类“弃真”的错误为第I类错误;当H0实际上为假时,做出接受H0的错误,称这类“取伪”的错误为第II类错误。把犯第I类错误的概率记作α,把犯第II类错误的概率记作β。因此,在确定检验法则时,应尽可能使犯这两类错误的概率都较小。一般来说,当样本容量固定时,如果减少犯一类错误的概率,则犯另一类错误的概率往往增大。如果要使犯两类错误的概率都减少,除非增加样本容量。
在给定样本容量的情况下,我们总是控制犯第I类错误的概率α,这种只对犯第I类错误的概率加以控制,而不考虑犯第II类错误的概率β的检验,称作显著性检验。概率α称为显著性水平,通常显著性水平的取值有α =0.05和0.025 ,代表着显著性检验的结论错误率必须低于5%、2.5%和1%。在统计学中,通常把在现实世界中发生几率小于5%的事件称之为“不可能事件”。
在显著性检验中,需要用到检验统计量,根据检验法来确定统计量,常用的统计量是Z统计量和t统计量。当检验统计量取某个区域C中的值时,拒绝原假设H0,则称区域C为拒绝域,拒绝域的边界点称为临界点。
处理参数的假设检验问题的步骤如下:
- 根据实际问题的要求,提出原假设H0和备择假设H1;
- 给定显著性水平α以及样本容量n;
- 确定检验统计量以及拒绝域的形式;
- 按P{当H0为真拒绝H0}<=α 求出拒绝域;
- 取样,根据样本观测值做出决策,是接受H0还是拒绝H0。
显著性检验通常分为两大类:临界值法和p值法。
参考文档:


