统计3：样本和统计量
统计推断是指，在数理统计中，我们研究的随机变量，其分布是未知的，或者是不完全知道的，人们是通过对所研究的随机变量进行重复独立的观察，得到许多观察值，对这些数据进行分析，从而对所研究的随机变量的分布做出种种推断。
一，随机样本
总体和个体 在数理统计中，研究对象是某一项数量指标（例如，学生的身高，体重等），对这一项数量指标进行观察。把试验的全部可能的观察值称为总体，每一个可能的观察值称为个体。
总体中的每一个个体是随机试验的一个观察值，因此，它是某一随机变量X的值。一个总体就对应一个随机变量X，对总体的研究就是对一个随机变量X的研究。
样本 在实际中，总体的分布一般是未知的，或只知道它具有某种形式而其中包含了未知参数。在数理统计中，人们都是通过从总体中抽取一部分个体，根据获得的数据对总体分布做出推断，被抽出的部分个体叫做总体的一个样本。
所谓从总体抽取一个个体，就是对总体X进行一次观察并记录观察结果。在相同的条件下对总体X进行n次重复的，独立的观察，把n次观察的结果按照试验的次序记为：X1,X2,...,Xn，
由于X1,X2,...,Xn是对随机变量X观察的结果，且各次观察是在相同的条件下独立进行的，所以有理由认为X1,X2,...,Xn是相互独立的，且都与X具有相同分布的随机变量，把X1,X2,...,Xn 称为来自总体X的一个简单随机样本。
当n次观察一经完成，得到一组实数x1,x2,...,xn，它们依次是随机变量X1,X2,...,Xn的观察值，称为样本值。
样本 定义， 设X是具有分布函数F的随机变量，若 X1,X2,...,Xn 是具有同一分布函数F的，相互独立的随机变量，则称 X1,X2,...,Xn 为从分布函数F（或总体F，总体X）得到的简单随机样本，简称样本。它们的观察值 x1,x2,...,xn称为样本值，又称为X的n个独立的观察值。
若 X1,X2,...,Xn 为总体X的一个样本，则X1,X2,...,Xn相互独立，且它们的分布函数都是F(x)，所以(X1,X2,...,Xn)的分布函数是：
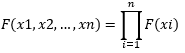
白话：随机变量X1,X2,...,Xn同时发生的概率是单独发生的概率之积。
二，统计量
样本是进行统计推断的依据，在应用时，往往不是直接使用样本本身，而是针对不同的指标构造样本的适当函数（即统计量），利用统计量进行统计推断。
1，统计量的定义
定义 设X1, X2, ..., Xn是来自总体X的一个样本，g(X1, X2, ..., Xn)是样本X1, X2, ..., Xn的函数，若g中不含未知数，则称 g(X1, X2, ..., Xn) 是一个统计量。
因为 X1, X2, ..., Xn 都是随机变量，而统计量g(X1, X2, ..., Xn)是随机变量的函数，因此统计量是一个随机变量。设x1，x2，...，xn是相应于样本X1，X2，...，Xn的样本值，则称g(x1，x2，...，xn)是g(X1, X2, ..., Xn)的观察值。
2，常用的统计量
统计量是随机变量的一个函数，是对样本的一个量化指标，常用的统计量是：
样本均值：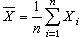
样本方差：
，注意是S2的分母是n-1
样本k阶矩，ak是原点距，mk是中心距：
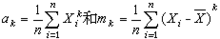
3，经验分布函数
经验分布函数是与总体分布函数F(x)相对应的统计量，也就是说，经验分布函数是一个统计量，只不过是随机变量X的分布函数的函数。
记经验分布函数Fn(x)=S(x)，表示X1, X2, ..., Xn中不大于x的随机变量的个数。
一般，设x1,x2,...,xn是总体F的一个容量为n的样本值，先将x1,x2,...,xn按照自小到大的次序排列，并重新编号，设为x(1) <= x(2)<=...<=x(n)
那么经验分布函数Fn(x)的观察值为：
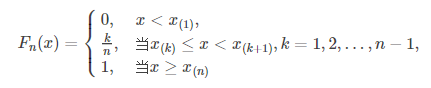
为什么 要定义经验分布函数呢？接下来介绍一个最重要的定理：格里纹科定理。
设x1,x2,...xn是取自总体分布函数为F(x)的样本，Fn(x)是其经验分布函数，当n→∞时，有
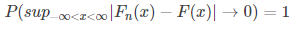
也即是说当n足够大时，经验分布函数是总体分布函数F(x)的一个良好的近似。格里纹科定理表明，当样本数足够多时，用样本估计总体是合理的，这即是数理统计的基础。
4，经验分布函数图形
求经验分布函数Fn(x)在一点x处的值，只要求出随机变量X的n个观测值(x1,x2,..,xn)中小于或等于x的个数，再除以观测次数n即可。由此可见，经验分布函数Fn(x)就是在n次重复独立实验中事件{X<=x}出现的频率。
经验分布函数Fn(x)的图形是一条呈跳跃上升的。
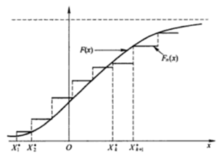
如果样本观测值(x1,x2,..,xn)中没有重复的数值，则每一跳跃为1/n。图中圆滑曲线是总体X的理论分布函数F(x)的图形。若把经验分布函数的图形连成折线，那么它实际就是累积频率直方图，这和概率分布函数的性质是一致的。
三，抽样分布
统计量的分布称为抽样分布，在使用统计量进行统计推断时，常需要直到它的分布。当总体的分布函数已知时，抽样分布是确定的，然而要求出统计量的精确分布，一般来说是困难的。
统计量的三大分布是指卡方分布（χ2分布）、t分布和F分布，是来自正态总体的三个常用的抽样分布，下文会详细介绍，此处略。
1，关于样本均值和方差的重要结论
设总体X(不管服从什么分布，只要均值和方差村子啊)的均值为μ，方差为σ； X1,X2,...,Xn是子来自总体X的一个样本，
和S2分别是样本均值和样本方差，
则有E()=μ，D()=σ2/n，E(S2)=σ2。
2，正态总体的样本均值与样本方差的分布
定理一：设 X1,X2,...,Xn是来自正态总体N(μ,σ2)的样本，那么是样本均值，则有
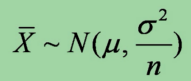
设统计量 Z，n为样本容量，μ为样本均值，S为样本标准差，
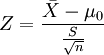
那么Z服从标准正态分布，即Z~N(0,1)，这就是在假设检验中用到的Z检验统计量。
定理二：设 X1,X2,...,Xn是来自正态总体N(μ,σ2)的样本，和S2分别是样本均值和样本方差，则有
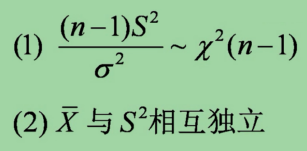
设卡方统计量χ2，那么该统计量服从卡方分布，即χ2~χ2(n-1)，这就是假设检验中经常用到得卡方检验统计量。
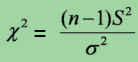
定理三：设 X1,X2,...,Xn是来自正态总体N(μ,σ2)的样本，和S2分别是样本均值和样本方差，则有
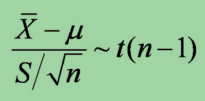
设统计量t，那么该统计量服从t分布，即t~t(n-1)，这就是假设检验中经常用到得t检验统计量。
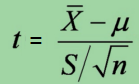
定理四：（两个正态总体的样本均值和样本方差的分布）
设X1,X2......Xn1和Y1,Y2..........Yn2分别是来自正态总体N(μ1,σ12)N(μ2,σ22)的样本，且这两个样本相互独立
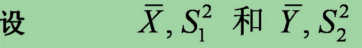
分别是这两个样本的样本均值和样本方差，则有
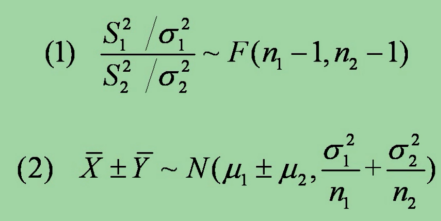
参考文档：
