DAX 第七篇:迭代函数
迭代是指逐行遍历表,访问一行叫做一次迭代,而每一次迭代得到的结果会作为下一次迭代的初始值。迭代函数至少拥有两个参数:
- 第一个参数:要遍历的行集
- 第二个参数:对同一行的不同字段要执行计算的表达式。
一,迭代函数计算的过程
最常见的迭代函数是SUMX函数,第一个参数Sales是要迭代的表或表值表达式,第二个参数是逐行计算的表达式:
SUMX( Sales, Sales[Quantity]*Sales[Net Price] )
迭代函数计算的过程:
Step1:要迭代的表或表值表达式受到筛选上下文的过滤,减少了数据表的总行数,也就是说,减少了迭代的次数,这个操作发生在迭代操作之前。
Step2:开始迭代,每一次迭代都会生成一个行上下文,在行上下文中计算表达式的值。
Step3:迭代函数把每一次迭代的结果聚合到一起,生成一个标量值作为结果返回。对于SUMX函数,是把每一次迭代的结果进行加和,最后返回总和。
二,迭代的基数
迭代的基数就是迭代操作执行的次数,要提高迭代函数的性能,需要减少迭代的基数。
对于以下DAX表达式,迭代的基数是Sales表的行数,Sales表的行数越多,迭代的基数越大。
SUMX( Sales, Sales[Quantity]*Sales[Net Price] )
对于嵌套的迭代函数,迭代的基数受到各个迭代函数的基数的影响,相当于多层嵌套的循环,每一层循环都要逐行遍历。
举个例子,对于以下嵌套的迭代函数,其执行的过程是:
SUMX(Product,
SUMX( RELATEDTABLE(Sales),
Sales[Quantity]* Product[Net Price])
)
第一步:计算外层的迭代函数,对Product表进行过滤,获得被迭代的数据行集1。
第二步:开始迭代,对于Product的每一行,都生成一个行上下文,并把行上下文传递给内层的迭代函数,
- 由于行上下文不执行筛选,不能直接使用关系( 原因一)
- 还由于内层的SUMX迭代函数,也不能把外层行上下文转换为筛选上下文(原因二),因此需要使用RELATEDTABLE函数,从Sales表中获取相关联的数据行集,作为内层迭代函数要执行迭代的数据行集2。
- 从Sales表中获取到相关联的数据行集2之后,开始执行内层SUMX的迭代计算,最终返回内层SUMX迭代计算的结果。
第三步:迭代“第二步”,直到遍历数据行集1的全部行,并把迭代的结果加和返回。
嵌套的迭代函数,代码不够简洁,优化之后的写法避免了迭代函数的嵌套,在DAX引擎中执行更为高效:
SUMX( Sales, Sales[Quantity]* RELATED(Product[Net Price]) )
三,在迭代函数中使用上下文转换
如果在行上下文中使用了CALCULATE函数或度量,那么行上下文会被转换为等价的筛选上下文。
详细过程,请阅读:DAX 第五篇:CALCULATE函数详解
附:分位数函数
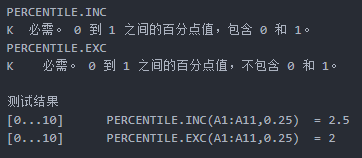
k表示期望的百分位值,其中INC是指inclusive(包含),EXC是指exclusive(不包含)。后缀带EXC的函数,参数k的取值范围是0-1,不包含0和1;后缀带INC的函数,参数k的取值范围是0-1,包含0和1。
PERCENTILE.EXC(<column>, <k>)
PERCENTILE.INC(<column>, <k>)
PERCENTILEX.EXC(<table>, <expression>, k)
PERCENTILEX.INC(<table>, <expression>, k)
当指定百分位数的值介于数组中的两个值之间时,这4个函数都会进行插值。 如果无法插入指定的k百分位数,则返回错误。
- 对于 INC函数,如果k不是1 /(n - 1)的倍数,则这4个函数将进行插值以确定第k个百分位数的值。
- 对于 EXC函数,如果k不是1 /(n + 1)的倍数,则这4个函数将进行插值以确定第k个百分位数的值。
PERCENTILE.INC
计算原理是:对于数组中的每个值,都会按照从小到大的顺序给定一个百分位(基于n-1),假如数组有n个数值,这n个百分位分别是:0/(n-1)、1/(n-1)、2/(n-1)……n-1/(n-1),当k值与这些百分位相同时,即k是1/(n-1)的倍数,直接返回数组中对应的数值,如果k不是 1/(n-1) 的倍数,则 PERCENTILE.INC 使用插值法来确定第k个百分点的值。
PERCENTILE.EXC
计算原理是:对于数组中的每个值,都会按照从小到大的顺序给定一个百分位(基于n+1),假如数组有n个数值,这n个百分位分别是:1/(n+1)、2/(n+1)、3/(n+1)……n/(n+1),当k值与这些百分位相同时,即k是1/(n+1)的倍数,直接返回数组中对应的数值,如果k不是 1/(n+1) 的倍数,则 PERCENTILE.EXC 使用插值法来确定第k个百分点的值。
引用简书上《 分位数计算,分析Excel中函数实现原理》的一个例子,作者是过桥0811 :

Python代码实现:

import math def percentile_inc(array,k): if len(array) == 0: return "数组不能为空" if k > 1 or k < 0: return "系数需为 0 到 1 之间的百分点值,包含 0 和 1" array_sort = sorted(array) address = (len(array_sort) - 1) * k + 1 if address == len(array_sort): return array_sort[len(array_sort) - 1] i = int(math.modf(address)[1]) #取出整数部分 j = math.modf(address)[0] #取出小数部分 value = array_sort[i-1] + (array_sort[i] - array_sort[i-1]) * j #print("数组为:" + str(array), "系数为:" + str(k),"百分位数为:" + str(value)) return value def percentile_exc(array,k): if len(array) == 0: return "数组不能为空" if k >= 1 or k <= 0: return "系数需为 0 到 1 之间的百分点值,不包含 0 和 1 " array_sort = sorted(array) address = (len(array_sort) + 1) * k if address < 1: return "因系数过小,不能通过插入值来确定指定的百分点的值" i = int(math.modf(address)[1]) #取出整数部分 j = math.modf(address)[0] #取出小数部分 value = array_sort[i-1] + (array_sort[i] - array_sort[i-1]) * j #print("数组为:" + str(array), "系数为:" + str(k),"百分位数为:" + str(value)) return value print(percentile_inc([10,9,8,7,6,5,4,3,2,1,0],0)) print(percentile_inc([10,9,8,7,6,5,4,3,2,1,0],0.01)) print(percentile_inc([10,9,8,7,6,5,4,3,2,1,0],0.25)) print(percentile_inc([10,9,8,7,6,5,4,3,2,1,0],1)) print(percentile_inc([1,3,2,4],0.3)) # 官网测试数据 print(percentile_exc([10,9,8,7,6,5,4,3,2,1,0],0)) print(percentile_exc([10,9,8,7,6,5,4,3,2,1,0],0.01)) print(percentile_exc([10,9,8,7,6,5,4,3,2,1,0],0.09)) print(percentile_exc([10,9,8,7,6,5,4,3,2,1,0],0.25)) print(percentile_exc([1,2,3,6,6,6,7,8,9],0.25)) # 官网测试数据
参考文档:



