转：方差分析——概念和原理
原文地址：《方差分析——概念和原理》
方差分析(analysis of variance)，简写为ANOVA，指的是利用对多个样本的方差的分析，得出总体均值是否相等的判定。本篇是我学习统计学的笔记，为了方便自己理解，也为了今后回顾能快速记忆起来。
案例说明
为了检验某小学六年级教学质量的差异，从该小学六年级的三个班级中分别选取一定数量的学生，分成三个组（三个样本），对他们期末考试的平均分进行统计分析。如果实验显示每个每组的均值相同，即三个班期末考试的成绩差异不大，则表明该小学六年级不同班级的教学质量没有差异，and vice versa。
每个样本组的平均分分别为 ，方差分别为
给出零假设 ：
备择假设 ：样本组的均值不全相等
方差分析将会依据观测数据判定假设是否成立。
进行方差分析有3个假定条件：
- 每个样本的值服从正态分布
- 每个样本的方差
相同
- 每个样本中的个体相互独立
假定零假设正确， ，三个样本均值相等，同时根据假定条件中的2：样本的方差相同，是不是可以看成——三个样本均取自均值
=
，方差为
的同一总体。
方差分析的核心是中心极限定理。
从均值为 ，方差为
的总体中抽取样本容量为
的样本组，每个样本组的均值服从均值
，方差
的正态分布。（中心极限定理）
这里需要澄清样本和总体的概念：总体有三个，分别是三个班级的所有学生，从三个总体中分别抽取出样本容量为n的三个集合，是我们所谓的样本。如下图
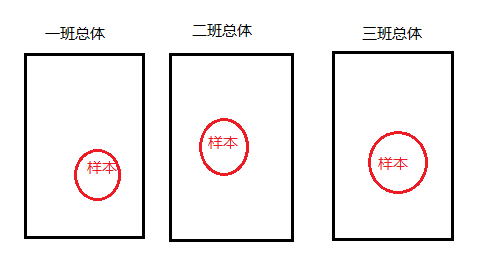
经过观测，如果样本的均值差异较大，可以推出，每个总体的均值不同；如果样本均值相等，每个总体的均值可能很接近。
这里的一个隐含推理就是：三个样本来自同一总体，即将整个六年级看做一个整体，不存在班级差异。这样，在抽取的样本量相同的假定条件下，抽样符合中心极限定理。可以推测样本均值的分布符合正态分布，在某一区间内的概率会大。
正态分布曲线
若 成立，我们所得的三个班级是这个曲线上的某三个点，正态分布的均值是三个样本的均值的平均数，即
，
正态分布的方差可用如下公式进行估计
，
其中 是样本数量，
是样本均值的方差。根据中心极限定理
，有
，即
可以证明这是样本方差的无偏估计，称为
的组间估计。
另一方面，如果 为假，则三个样本来自不同的总体
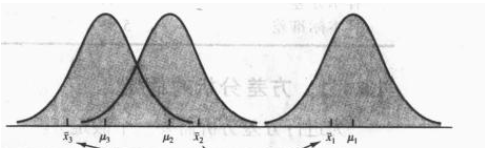三个样本来自不同总体
有三个不同的分布。如果将三个班看做一个总体，则总体的方差也会更大，总体的方差可用三个样本方差的均值来估计：
，称为
的组内估计。
如果 不成立，组内估计可用于总体的方差估计。因为当
成立时，每个样本的方差相同，等于总体方差，此时方差的组间估计是更好的估计。故当组内估计和组间估计接近时，
为真。这就是方差分析的核心思路。
正式声明
设有 组样本，每组有
个独立样本，
表示每组中的第几个样本，
表示第几个样本组。
定义零假设 ：
对应的备择假设 ：样本均值不完全相等
可以计算每组的均值 （其中
为第
组的第
个样本）
每组方差
若k个样本来自同一总体，该总体的均值等于所有样本中的样本个体之和除以总个体数 ，另一种方法是样本均值的均值
总体方差的组间估计为
总体方差的组内估计为
有了上面一段啰里啰嗦的公式之后，F检验的正式说明是：如果零假设为真，总体方差的组间估计和组内估计的比值，服从分子自由度为 ，分母自由度为
的F分布
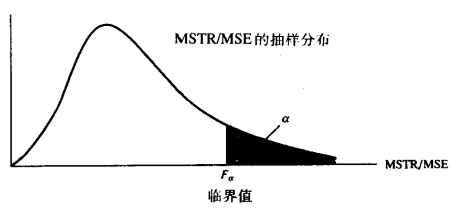F分布和当中的拒绝域
应用
给定显著性水平 ，F分布对应的临界值为
，当
时，拒绝
原文地址：
