codeforces766E Mahmoud and a xor trip(按位统计+树形DP)
本文版权归ljh2000和博客园共有,欢迎转载,但须保留此声明,并给出原文链接,谢谢合作。
本文作者:ljh2000
作者博客:http://www.cnblogs.com/ljh2000-jump/
转载请注明出处,侵权必究,保留最终解释权!
Description
Mahmoud and Ehab live in a country with n cities numbered from 1 to n and connected by n - 1 undirected roads. It's guaranteed that you can reach any city from any other using these roads. Each city has a number ai attached to it.
We define the distance from city x to city y as the xor of numbers attached to the cities on the path from x to y (including both x andy). In other words if values attached to the cities on the path from x to y form an array p of length l then the distance between them is  , where
, where  is bitwise xor operation.
is bitwise xor operation.
Mahmoud and Ehab want to choose two cities and make a journey from one to another. The index of the start city is always less than or equal to the index of the finish city (they may start and finish in the same city and in this case the distance equals the number attached to that city). They can't determine the two cities so they try every city as a start and every city with greater index as a finish. They want to know the total distance between all pairs of cities.
The first line contains integer n (1 ≤ n ≤ 105) — the number of cities in Mahmoud and Ehab's country.
Then the second line contains n integers a1, a2, ..., an (0 ≤ ai ≤ 106) which represent the numbers attached to the cities. Integer ai is attached to the city i.
Each of the next n - 1 lines contains two integers u and v (1 ≤ u, v ≤ n, u ≠ v), denoting that there is an undirected road between cities u and v. It's guaranteed that you can reach any city from any other using these roads.
Output one number denoting the total distance between all pairs of cities.
3
1 2 3
1 2
2 3
10
5
1 2 3 4 5
1 2
2 3
3 4
3 5
52
5
10 9 8 7 6
1 2
2 3
3 4
3 5
131
A bitwise xor takes two bit integers of equal length and performs the logical xor operation on each pair of corresponding bits. The result in each position is 1 if only the first bit is 1 or only the second bit is 1, but will be 0 if both are 0 or both are 1. You can read more about bitwise xor operation here: https://en.wikipedia.org/wiki/Bitwise_operation#XOR.
In the first sample the available paths are:
- city 1 to itself with a distance of 1,
- city 2 to itself with a distance of 2,
- city 3 to itself with a distance of 3,
- city 1 to city 2 with a distance of
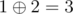 ,
, - city 1 to city 3 with a distance of
 ,
, - city 2 to city 3 with a distance of
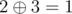 .
.
正解:按位统计+树形DP
解题报告:
题目要求在一棵带权树上的两两路径上点权异或和的总和。
对于这种位运算的题目,我们的想法必然是按位考虑的,因为位与位之间彼此独立,可以单独考虑。
那么拆成每一位之后,题目变成了统计0和1两种情况的组合的数目,最后乘2的幂次即可。f[x][0、1]表示x这一位为0、1时的数量,考虑我们可以每次把之前做完的子树与其父亲节点合并,然后再与当前节点组合计算贡献。
值得一提的是,有必要注意一下向上转移的细节。如果x的这一位是0,显然没有影响;但是如果这一位是1,就会导致往上异或之后改变一下,需要注意。
//It is made by ljh2000
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <string>
#include <complex>
using namespace std;
typedef long long LL;
const int MAXN = 100011;
const int MAXM = 200011;
int n,a[MAXN],first[MAXN],ecnt,to[MAXM],next[MAXM];
LL ans,f[MAXN][2],now;
inline int getint(){
int w=0,q=0; char c=getchar(); while((c<'0'||c>'9') && c!='-') c=getchar();
if(c=='-') q=1,c=getchar(); while (c>='0'&&c<='9') w=w*10+c-'0',c=getchar(); return q?-w:w;
}
inline void dfs(int x,int fa,int wei){
int pos=a[x]>>wei; pos=pos&1;
f[x][pos]=1; f[x][pos^1]=0;
for(int i=first[x];i;i=next[i]) {
int v=to[i]; if(v==fa) continue;
dfs(v,x,wei);
ans+=f[v][pos]*f[x][pos^1]*now;
ans+=f[v][pos^1]*f[x][pos]*now;
if(pos==0) {
f[x][pos]+=f[v][pos];
f[x][pos^1]+=f[v][pos^1];
}
else {
f[x][pos^1]+=f[v][pos];
f[x][pos]+=f[v][pos^1];
}
}
}
inline void work(){
n=getint(); for(int i=1;i<=n;i++) a[i]=getint(),ans+=a[i]; int x,y;
for(int i=1;i<n;i++) {
x=getint(); y=getint();
next[++ecnt]=first[x]; first[x]=ecnt; to[ecnt]=y;
next[++ecnt]=first[y]; first[y]=ecnt; to[ecnt]=x;
}
for(int i=0;i<=20;i++) {
now=(1<<i);
dfs(1,0,i);
}
printf("%lld",ans);
}
int main()
{
work();
return 0;
}


