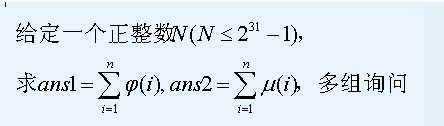BZOJ3944 Sum

本文版权归ljh2000和博客园共有，欢迎转载，但须保留此声明，并给出原文链接，谢谢合作。

 

 

 

本文作者：ljh2000
作者博客：http://www.cnblogs.com/ljh2000-jump/
转载请注明出处，侵权必究，保留最终解释权！

 

 

Description

 

Input

一共T+1行

第1行为数据组数T(T<=10)

第2~T+1行每行一个正整数N，代表一组询问

 

 

 

Output

一共T行，每行两个用空格分隔的数ans1,ans2

 

 

Sample Input

6
1
2
8
13
30
2333

Sample Output

1 1
2 0
22 -2
58 -3
278 -3
1655470 2

 

 

正解：线性筛+杜教筛

解题报告：

　　这道题是杜教筛模板题，在笔记本上推了两遍才开始写......

　　

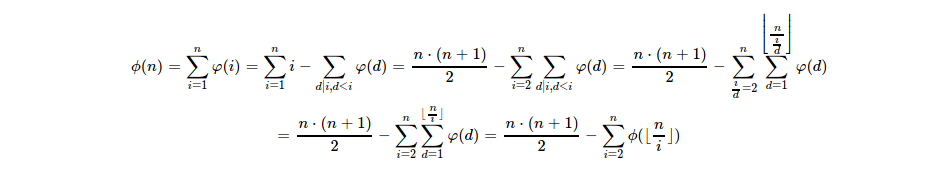
　　显然后面那一坨可以记忆化搜索。

　　另外因为无法用数组存下来（此时$\frac{n}{i}$大于等于$n^{\frac{2}{3}}$），所以我们考虑用分子（即$i$，显然小于等于$n^{\frac{1}{3}}$）表示这个分数所代表的欧拉函数前缀和，即可避开存不下的尴尬问题。　　

　　ps:我讨厌$2^{31}-1$！！！！！！！！看看我代码中的unsigned int就懂了。

　　

 

//It is made by ljh2000
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef unsigned int uint;
const int MAXN = 5400011;
const int m = 5400000;
const int MAXM = 100011;
int n,prime[MAXN],cnt;
LL mobius[MAXN],phi[MAXN];
LL ans_phi[MAXM],ans_mo[MAXM];
bool vis[MAXN],visp[MAXM],vism[MAXM];
inline int getint(){
    int w=0,q=0; char c=getchar(); while((c<'0'||c>'9') && c!='-') c=getchar();
    if(c=='-') q=1,c=getchar(); while (c>='0'&&c<='9') w=w*10+c-'0',c=getchar(); return q?-w:w;
}

inline void init(){
	mobius[1]=1; phi[1]=1;
	for(int i=2;i<=m;i++) {
		if(!vis[i]) { prime[++cnt]=i; mobius[i]=-1; phi[i]=i-1; }
		for(int j=1;j<=cnt && (LL)i*prime[j]<=m;j++) {
			vis[i*prime[j]]=1;
			if(i%prime[j]==0) { phi[i*prime[j]]=phi[i]*prime[j]; mobius[i*prime[j]]=0; break; }
			else { phi[i*prime[j]]=phi[i]*phi[prime[j]]; mobius[i*prime[j]]=-mobius[i]; }
		}
	}
	for(int i=2;i<=m;i++) mobius[i]+=mobius[i-1],phi[i]+=phi[i-1];
}

inline LL get_phi(uint now){
	if(now<=m) return phi[now];
	int nn=n/now,nex; if(visp[nn]) return ans_phi[nn];
	LL sav=(LL)now*(now+1)>>1;  
	for(uint i=2;i<=now;i=nex+1) {
		nex=now/(now/i);
		sav-=get_phi(now/i/*!!!*/)*(nex-i+1);
	}
	visp[nn]=1;
	ans_phi[nn]=sav;
	return sav;
}

inline LL get_mo(uint now){
	if(now<=m) return mobius[now];
	int nn=n/now,nex; if(vism[nn]) return ans_mo[nn];
	LL sav=1;
	for(uint i=2;i<=now;i=nex+1) {
		nex=now/(now/i);
		sav-=get_mo(now/i/*!!!*/)*(nex-i+1);
	}
	vism[nn]=1;/*!!!*/
	ans_mo[nn]=sav;
	return sav;
}

inline void work(){
	int T=getint(); init(); 
	while(T--) {
		n=getint(); memset(visp,0,sizeof(visp)); memset(vism,0,sizeof(vism));
		LL ans1=get_phi(n); LL ans2=get_mo(n);
		printf("%lld %lld\n",ans1,ans2);	   
	}
}

int main()
{
    work();
    return 0;
}