BZOJ3434 [Wc2014]时空穿梭
本文版权归ljh2000和博客园共有,欢迎转载,但须保留此声明,并给出原文链接,谢谢合作。
本文作者:ljh2000
作者博客:http://www.cnblogs.com/ljh2000-jump/
转载请注明出处,侵权必究,保留最终解释权!
Description

Input
第一行包含一个正整数T,表示有T组数据求解
每组数据包含两行,第一行包含两个正整数N,C(c>=2),分别表示空间的
维数和需要选择的暂停点个数
第二行包含N个正整数,依次表示M1,M2....Mn
Output
有T行,每行一个非负整数,依次对应每组数据的答案。
Sample Input
2 3
3 4
3 3
3 4 4
4 4
5 9 7 8
Sample Output
4
846
HINT
样例数据第一组共有两种可行方案:一种是选择(1,1),( 2,2) ,( 3,3) ,另一种是选择 ( 1,2) ,( 2,3) ,( 3,4) 。
T<=1000,N<=11,C<=20,Mi<=100000
正解:莫比乌斯反演+组合数学
解题报告:
下面摘自我校学长rhl的solution:

到这一步应该是很好推的,然而我并没有一开始就想出来。
第一行是原始的式子,然后我们考虑变枚举每个△x的值,枚举每个gcd(不妨设为g)的贡献,则可得到第二行式子,注意这个式子满足当且仅当每个△x的gcd为1;
第二行到第三行是莫比乌斯函数的应用:莫比乌斯函数前缀和为1当且仅当n=1。显然前缀和为1的时候说明t只能取1,也就是说△x的gcd为1。
下面是进一步的推导:
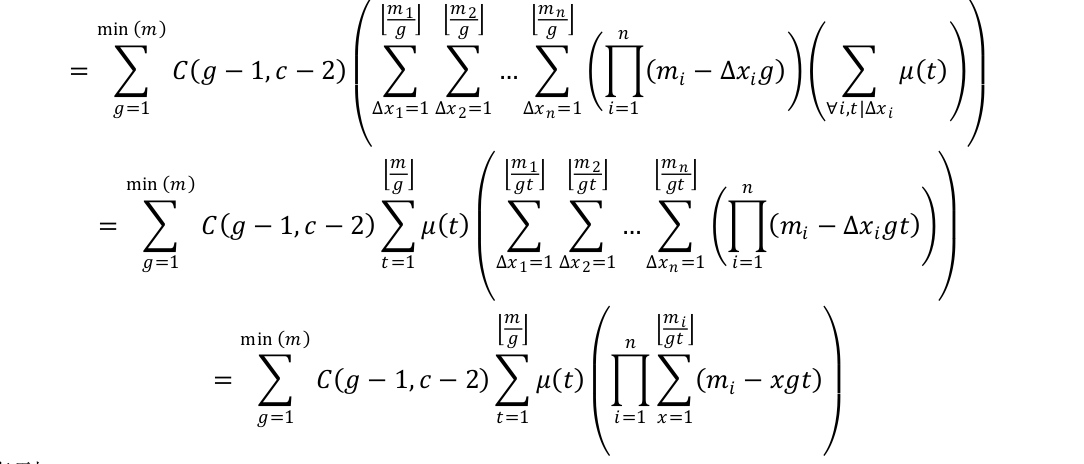
容易发现从图中第一行到第二行是提出了t,提出t的方式我们可以这样理解:
把t的莫比乌斯函数前缀和看成一个整体,那么我枚举△x再枚举t,可以等价于先枚举t再去枚举当前的这个t所产生的贡献,所以△x的范围中再用t去约束。而因为t的最大值肯定是在最小的那个m中取到,所以最大值就是$\left\lfloor\frac{m}{g}\right\rfloor$。
第二行到第三行,相当于是用了一次乘法分配律。可以想象有n列数,每列数就是对应着每个△x的取值范围,第二行的那一块相当于是每一列中取一个数然后一一对应,就可以变成每个数先加起来再乘。以$n=2$为例,△x1取第一个值的时候,△x2可以取第二列的所有值,然后△x1的这一个值和所有的△x2的取值分别组合,就可以先对于△x2求和再乘上△x1的那个唯一取值即可,而每个△x1的取值都是对应的与每个△x2组合,所以△x1的部分也可以求和。就变成了上面的式子长得那样。
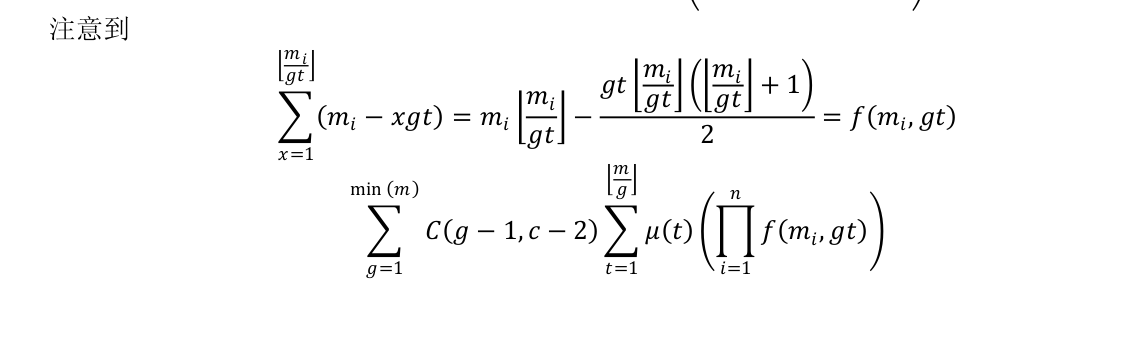

第二行到第三行,同样可以理解成乘法分配率。不难想象,拆开之后每一项都是形如$f$项的未知数是$gt$,组合数C的是$g$,莫比乌斯函数μ的是$t$。那么我可以采用惯用策略:计算$f$项的贡献,不妨设$h=g*t$,同时枚举一个$g$,那么$h/g$就是原来的$t$,想想就会发现这样可以覆盖到所有的情况,也就是说这样枚举的话就可以把$h$项的贡献计算完成了。
得到第五行的式子之后,就可以得到一个$O(nm)$的算法,看了看数据范围,应该有$60$分了。然而我试了试只有50分,看来我也变成常数boy了。
接下来我们考虑如何优化上式:


如图中所述,函数是由若干段构成的,那么每一段都可以一起计算,最后加在一起就可以了。
到此为止就算over了。
总结一下:
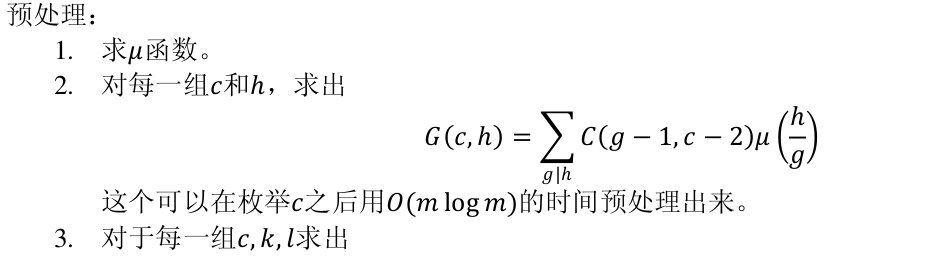

推导+调试用了我两天时间!!!一把辛酸泪
//It is made by ljh2000
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <string>
using namespace std;
typedef long long LL;
const int MAXN = 12;
const int inf = (1<<30);
const int MAXL = 100011;
const int MAXM = 4000011;
const int MOD = 10007;
int n,c,m[MAXN],prime[MAXL],Mc,mobius[MAXL],cnt,mn,mx,C[MAXL][21],ans,G[21][MAXL],f[21][12][MAXL],a[MAXN];
bool vis[MAXL];
namespace save{ int n[1011],c[1011]; int m[1011][12]; }
inline void MO(int &x){ if(x>MOD) x%=MOD; else if(x<-MOD) x%=MOD; }
inline int getint(){
int w=0,q=0; char c=getchar(); while((c<'0'||c>'9') && c!='-') c=getchar();
if(c=='-') q=1,c=getchar(); while (c>='0'&&c<='9') w=w*10+c-'0',c=getchar(); return q?-w:w;
}
inline void init(){
mobius[1]=1; int lim=Mc-2,x;
for(int i=2;i<=mx;i++) {//线性筛+递推莫比乌斯函数
if(!vis[i]) { mobius[i]=-1; prime[++cnt]=i; }
for(int j=1;j<=cnt&&i*prime[j]<=mx;j++) {
vis[i*prime[j]]=1;
if(i%prime[j]) mobius[i*prime[j]]=-mobius[i];
else { mobius[i*prime[j]]=0; break; }
}
}
C[0][0]=1; for(int i=1;i<=mx;i++){ C[i][0]=1; for(int j=1;j<=lim;j++) C[i][j]=C[i-1][j-1]+C[i-1][j],MO(C[i][j]); }
for(int cc=2;cc<=Mc;cc++) {//预处理G数组,G[cc][i]表示c=cc、h=i时的G(h)的值
for(int i=1;i<=mx;i++) {
for(int j=i,ci=1;j<=mx;j+=i,ci++) {
G[cc][j]+=C[i-1][cc-2]*mobius[ci];
MO(G[cc][j]);
}
}
}
for(int h=1;h<=mx;h++) {//f[cc][j][i]表示G(h)*h^j中1到h的前缀和,固定指数!
for(int cc=1;cc<=Mc;cc++) {
x=1;
for(int j=0;j<=11;j++) {
f[cc][j][h]=G[cc][h]*x+f[cc][j][h-1]; MO(f[cc][j][h]);
x*=h; MO(x);
}
}
}
}
inline void cal(int h){//若干个形如(px+q)的一次式相乘
int x1,x0,t; memset(a,0,sizeof(a)); a[0]=1;//初始化
for(int i=1;i<=n;i++) {
t=(m[i]/h);
x1=( -(LL)t*(t+1)/2 )%MOD;//计算p,注意有一个负号
x0=( (LL)m[i]*t )%MOD;//计算q
for(int j=n;j>=1;j--)
a[j]=a[j]*x0+a[j-1]*x1,MO(a[j]);//第j次项可以由上次的第j-1次项*px,也可以由上次的第j项*q得到
a[0]=a[0]*x0;//0次项单独考虑
MO(a[0]);
}
}
inline void work(){
int T=getint();
for(int o=1;o<=T;o++) {
save::n[o]=getint(),save::c[o]=getint(); Mc=max(save::c[o],Mc);
for(int i=1;i<=save::n[o];i++) save::m[o][i]=getint(),mx=max(mx,save::m[o][i]);
}
init();
for(int o=1;o<=T;o++) {
n=save::n[o]; c=save::c[o]; mn=inf;//最小的m
for(int i=1;i<=n;i++) m[i]=save::m[o][i],mn=min(mn,m[i]);
ans=0; int nex;
for(int i=1;i<=mn;i=nex+1) {
nex=mn; for(int j=1;j<=n;j++) nex=min(nex,m[j]/(m[j]/i));
cal(i); for(int j=0;j<=n;j++) ans+=a[j]*(f[c][j][nex]-f[c][j][i-1]),MO(ans);
}
ans%=MOD; ans+=MOD; ans%=MOD;
printf("%d\n",ans);
}
}
int main()
{
work();
return 0;
}

