BZOJ1005 [HNOI2008]明明的烦恼

Description

　　自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?

Input

　　第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1

Output

　　一个整数,表示不同的满足要求的树的个数,无解输出0

Sample Input

3
1
-1
-1

Sample Output

2

HINT

　　两棵树分别为1-2-3;1-3-2

 

正解：purfer 序列+组合数学+高精度

解题报告：

　　我是看的一篇极其详细的博客看懂的，我还是太弱了，组合数学都不熟练。。。

　　传送门：http://www.cnblogs.com/zhj5chengfeng/archive/2013/08/23/3278557.html

 

（我是题解的搬运工）：

这题需要了解一种数列： Purfer Sequence

我们知道，一棵树可以用括号序列来表示，但是，一棵顶点标号（1~n）的树，还可以用一个叫做 Purfer Sequence 的数列表示

一个含有 n 个节点的 Purfer Sequence 有 n-2 个数，Purfer Sequence 中的每个数是 1~n 中的一个数

 

一个定理：一个 Purfer Sequence 和一棵树一一对应

 

先看看怎么由一个树得到 Purfer Sequence

由 一棵树得到它的 Purfer Sequence 总共需要 n-2 步，每一步都在当前的树中寻找具有最小标号的叶子节点（度为 1），将与其相连的点的标号设为 Purfer Sequence 的第 i 个元素，并将此叶子节点从树中删除，直到最后得到一个长度为 n-2 的 Purfer Sequence 和一个只有两个节点的树

 

看看下面的例子：

假设有一颗树有 5 个节点，四条边依次为：(1, 2), (1, 3), (2, 4), (2, 5)，如下图所示：

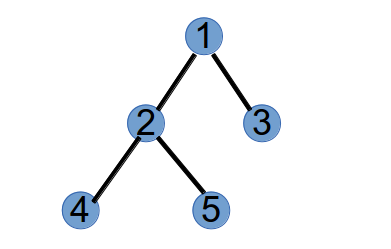
第 1 步，选取具有最小标号的叶子节点 3，将与它相连的点 1 作为第 1 个 Purfer Number，并从树中删掉节点 3：

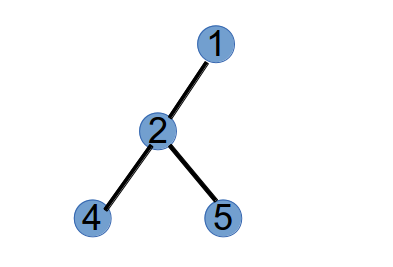
第 2 步，选取最小标号的叶子节点 1，将与其相连的点 2 作为第 2 个 Purfer Number，并从树中删掉点 1：

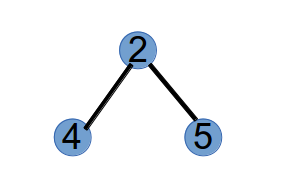
第 3 步，选取最小标号的叶子节点 4，将与其相连的点 2 作为第 3 个 Purfer Number，并从树中删掉点 4：

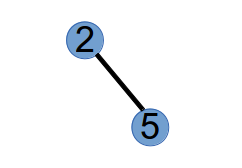
最后，我们得到的 Purfer Sequence 为：1 2 2

不难看出，上面的步骤得到的 Purfer Sequence 具有唯一性，也就是说，一个树，只能得到一个唯一的 Purfer Sequence

 

接下来看，怎么由一个 Purfer Sequence 得到一个树

由 Purfer Sequence 得到一棵树，先将所有编号为 1 到 n 的点的度赋初值为 1，然后加上它在 Purfer Sequence 中出现的次数，得到每个点的度

先执行 n-2 步，每一步，选取具有最小标号的度为 1 的点 u 与 Purfer Sequence 中的第 i 个数 v 表示的顶点相连，得到树中的一条边，并将 u 和 v 的度减一

最后再把剩下的两个度为 1 的点连边，加入到树中

 

我们可以根据上面的例子得到的 Purfer Sequence ：1 2 2 重新得到一棵树

Purfer Sequence 中共有 3 个数，可以知道，它表示的树中共有 5 个点，按照上面的方法计算他们的度为下表所示：

 

顶点	1	2	3	4	5
度	2	3	1	1	1

 

 

 

第 1 次执行，选取最小标号度为 1 的点 3 和 Purfer Sequence 中的第 1 个数 1 连边：

将 1 和 3 的度分别减一：

 

顶点	1	2	3	4	5
度	1	3	0	1	1

 

 

 

第 2 次执行，选取最小标号度为 1 的点 1 和 Purfer Sequence 中的第 2 个数 2 连边：

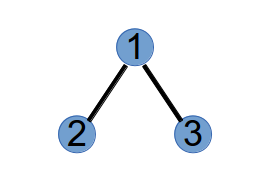
将 1 和 2 的度分别减一：

 

顶点	1	2	3	4	5
度	0	2	0	1	1

 

 

 

第 3 次执行，将最小标号度为 1 的点 4 和 Purfer Sequence 第 3 个数 2 连边：

将 2 和 4 的度分别减一：

 

顶点	1	2	3	4	5
度	0	1	0	0	1

 

 

 

最后，还剩下两个点 2 和 5 的度为 1，连边：

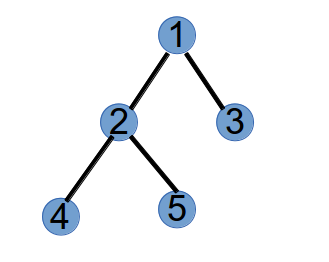
至此，一个 Purfer Sequence 得到的树画出来了，由上面的步骤可知，Purfer Sequence 和一个树唯一对应

综上，一个 Purfer Sequence 和一棵树一一对应

 

有了 Purfer Sequence 的知识，这题怎么搞定呢？

 

先不考虑无解的情况，从 Purfer Sequence 构造树的过程中可知，一个点的度数减一表示它在 Purfer Sequence 中出现了几次，那么：

假设度数有限制的点的数量为 cnt，他们的度数分别为：d[i]

另：

 

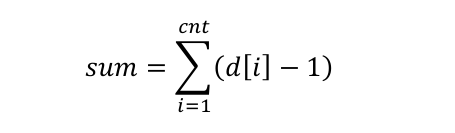
那么，在 Purfer Sequence 中的不同排列的总数为：

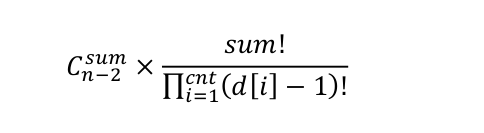
而剩下的 n-2-sum 个位置，可以随意的排列剩余的 n-cnt 个点，于是，总的方案数就应该是：

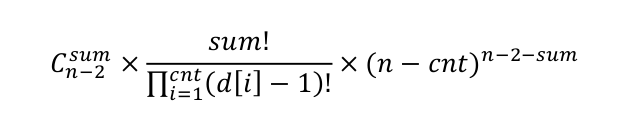
化简之后为：

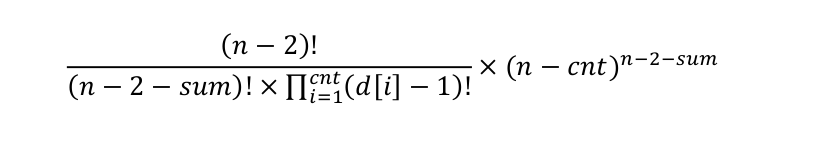
在有解的情况下，计算该结果输出就行了

 

备注：注意在prufer序列中不出现意味着度数为1！！！

 

 

//It is made by jump~
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <set>
#ifdef WIN32   
#define OT "%I64d"
#else
#define OT "%lld"
#endif
using namespace std;
typedef long long LL;
const int MAXN = 1011;
const int MOD = 1000000;
int n,d[MAXN],sum,cnt;
int prime[MAXN]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,443,449,457,461,463,467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,593,599,601,607,613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,719,727,733,739,743,751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,857,859,863,877,881,883,887,907,911,919,929,937,941,947,953,967,971,977,983,991,997};
int tong[MAXN];
int gao[MAXN];

inline int getint()
{
       int w=0,q=0;
       char c=getchar();
       while((c<'0' || c>'9') && c!='-') c=getchar();
       if (c=='-')  q=1, c=getchar();
       while (c>='0' && c<='9') w=w*10+c-'0', c=getchar();
       return q ? -w : w;
}

inline void divide(int x,int type){
    if(x==0||x==1) return ; 
    for(int j=0;j<=167;j++) {
    if(x<=1) break;
    while(x%prime[j]==0) tong[j]+=type,x/=prime[j];
    }
}

inline void work(){
    n=getint(); bool ok=true;
    for(int i=1;i<=n;i++) {
    d[i]=getint();
    if(d[i]==0 || d[i]>n-1) ok=false;
    if(d[i]>0)   sum+=d[i]-1,cnt++;
    }
    if(n==1) { if(!d[1]) printf("1"); else printf("0"); return ; }
    if(sum>n-2){ printf("0");return ;}
    if(!ok) { printf("0"); return ; } 
    for(int i=n-2-sum+1;i<=n-2;i++) divide(i,1);       
    for(int i=1;i<=n;i++) 
    if(d[i]>0){
        for(int j=1;j<=d[i]-1;j++) divide(j,-1);
    }
    
    int kuai=1; gao[kuai]=1; 
    for(int i=1;i<=n-2-sum;i++) {
    for(int j=1;j<=kuai;j++) gao[j]*=(n-cnt);
    for(int j=1;j<=kuai;j++) if(gao[j]>=MOD)  gao[j+1]+=gao[j]/MOD,gao[j]%=MOD;
    while(gao[kuai+1]) gao[kuai+1]+=gao[kuai]/MOD,gao[kuai]%=MOD,kuai++;
    }
    for(int i=0;i<=167;i++) {
    while(tong[i]) {
        for(int j=1;j<=kuai;j++) gao[j]*=prime[i];        
        for(int j=1;j<=kuai;j++) if(gao[j]>=MOD) gao[j+1]+=gao[j]/MOD,gao[j]%=MOD;
        while(gao[kuai+1]) gao[kuai+1]+=gao[kuai]/MOD,gao[kuai]%=MOD,kuai++;
        tong[i]--;
    }
    }
    printf("%d",gao[kuai]);
    for(int i=kuai-1;i>=1;i--) printf("%06d",gao[i]);
}

int main()
{
  work();
  return 0;
}