POJ2286 The Rotation Game

 

 

Description

The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind. 

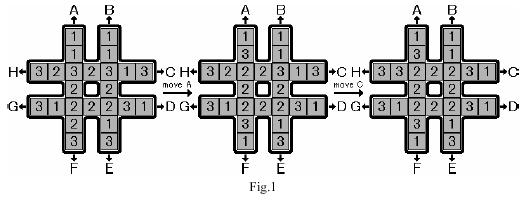
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration. 

Input

The input consists of no more than 30 test cases. Each test case has only one line that contains 24 numbers, which are the symbols of the blocks in the initial configuration. The rows of blocks are listed from top to bottom. For each row the blocks are listed from left to right. The numbers are separated by spaces. For example, the first test case in the sample input corresponds to the initial configuration in Fig.1. There are no blank lines between cases. There is a line containing a single `0' after the last test case that ends the input. 

Output

For each test case, you must output two lines. The first line contains all the moves needed to reach the final configuration. Each move is a letter, ranging from `A' to `H', and there should not be any spaces between the letters in the line. If no moves are needed, output `No moves needed' instead. In the second line, you must output the symbol of the blocks in the center square after these moves. If there are several possible solutions, you must output the one that uses the least number of moves. If there is still more than one possible solution, you must output the solution that is smallest in dictionary order for the letters of the moves. There is no need to output blank lines between cases. 

Sample Input

1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0

Sample Output

AC
2
DDHH
2

Source

Shanghai 2004

 

正解：迭代加深搜索（+大剪枝）

解题报告：

　　北大信息学夏令营一试第一题，当时考场上看没什么人做于是果断没做，考完再看才发现是个搜索题。

　　今天考试居然考到了这道题，好吧，就来填这个坑吧。

      首先迭代加深，确定搜索深度上界（保证dfs不会gi），然后我们考虑各种奇奇怪怪的剪枝。

　　显然，我们会在最终得到中间的一圈全是1或2或3，不妨取一个目前已经数量最多的数字来做一个估价若已经超过上界，就直接返回。

　　还有一个剪枝，如果上一次往上移动，那么这一次就不要往下移动。

　　代码如下：

 

//It is made by jump~
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#ifdef WIN32   
#define OT "%I64d"
#else
#define OT "%lld"
#endif
using namespace std;
typedef long long LL;
/*
图形一览：
         0     1
         2     3
 4   5   6  7  8  9  10
        11    12
13  14  15 16 17 18  19
        20    21
    22    23
*/
int num[8][7]={{0,2,6,11,15,20,22},{1,3,8,12,17,21,23},{10,9,8,7,6,5,4},{19,18,17,16,15,14,13}};
int ying[13]={5,4,7,6,1,0,3,2};
int center[8]={6,7,8,11,12,15,16,17};
int a[45];
int ans,sh;
char out[45];

inline int getint()
{
       int w=0,q=0;
       char c=getchar();
       while((c<'0' || c>'9') && c!='-') c=getchar();
       if (c=='-')  q=1, c=getchar();
       while (c>='0' && c<='9') w=w*10+c-'0', c=getchar();
       return q ? -w : w;
}

inline bool check(){
    int xun=a[center[0]];
    for(int i=1;i<=7;i++) if(a[center[i]]!=xun) return false;
    return true;
}

inline void mov(int x){
    int cun=a[num[x][0]];
    for(int i=0;i<=5;i++) {
    a[num[x][i]]=a[num[x][i+1]];
    }
    a[num[x][6]]=cun;
}

inline int count(int x){
    int total=0;
    for(int i=0;i<=7;i++) if(a[center[i]]!=x) total++;
    return total;
}

inline int gu(){
    return min( min(count(1),count(2)) , count(3));
}

inline void init(){
    for(int i=4;i<=7;i++) for(int j=0;j<=6;j++) num[i][j]=num[ying[i]][6-j];
    ying[12]=45;
}

inline bool dfs(int tim,int limit,int last){
    if(check()){
    //out[tim]=a[center[0]];
    sh=a[center[0]];
    return true;
    }
    else {
    if(gu()+tim>limit) return false;
    for(int i=0;i<8;i++) {
        if(ying[last]==i) continue;
        out[tim]='A'+i;
        mov(i);
        if(dfs(tim+1,limit,i)) return true;
        mov(ying[i]);
    }
    }
    return false;
}

inline void solve(){
    init();
    while(1){
    a[0]=getint();
    if(!a[0]) break;
    for(int i=1;i<=23;i++) a[i]=getint();

    if(check()) printf("No moves needed\n%d\n",a[center[0]]); 
    else{
        for(ans=1;;ans++) {
        if(dfs(0,ans,12)) break;
        }    
        printf("%s",out);
        printf("\n%d\n",sh);
    }
    memset(out,'\0',sizeof(out));
    }
}

int main()
{
  solve();
  return 0;
}