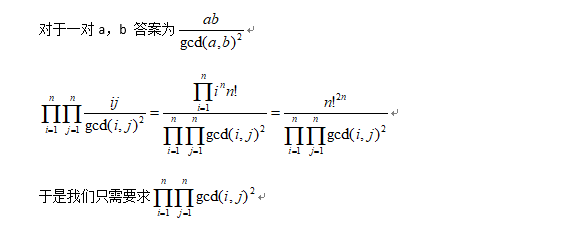HGOI 20181101题解

/*
又是爆0的一天（不知道今年高考难不难，反正今天(信息学)真的难！）
*/

solution：对于两个数相加，有一个显然的结论就是要么不进位（相对于位数大的），要么（进最多一位）

然后对于整个数组先排序，然后枚举每一个数，在它的前面找到和他相加进1位的点，讨论不变位和进一位累加求和即可

由于数列有序对于最左边的p满足f(a[p]+a[now])=f(a[now])+1对于他的右边所有的数都符合进一位的条件，这样可以二分查找找到最左端的点

# pragma GCC optimze(2)
# include<bits/stdc++.h>
# define int long long
using namespace std;
const int MAXN=1e6+10;
int n,a[MAXN];
inline int read()
{
    int X=0,w=0;char c=0;
    while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar();
    while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar();
    return w?-X:X;
}
int fun(int x)
{
    int ret=0;
    while (x){ ret++; x/=10;}
    return ret;
}
int find(int sl,int sr,int id)
{
    int l=sl,r=sr,ans=-1;
    int tmp=fun(a[id])+1;
    while (l<=r) {
        int mid=(l+r)/2;
        if (fun(a[mid]+a[id])==tmp) r=mid-1,ans=mid;
        else l=mid+1;
    }
    return ans;
}
signed main()
{
    n=read(); 
    for (int i=1;i<=n;i++) a[i]=read();
    sort(a+1,a+1+n);
    int ans=0;
    for (int i=2;i<=n;i++) {
        int p=find(1,i-1,i),tmp=fun(a[i]);
        if (p==-1) ans+=tmp*(i-1);
        else ans+=(tmp+1)*(i-p)+tmp*(p-1);
    }
    cout<<ans<<endl;
    return 0;
 }

solution：这个题有一个结论，就是对于全集U={所有人}的2ⁿ个子集，存在tot个满足下面关系的子集

子集中所有的权重加起来不足m，但是从其他不选的人随便拿一个放入子集权重都能大于等于m，最终统计出的tot就是答案

也就是最少需要锁的个数。

上面的结论是我们构造出来的，然后我们需要证明这个结论。

现在首先是两个性质的事情，

数学上我们定义：

• 证明条件：通过所有的证明条件推出一个结论的条件全集。
• 必要条件：是证明条件的子集,所有的必要条件的全集就是证明条件，无论是什么证明方法，都需要的条件。
• 充分条件：证明条件是充分条件的子集，也就是满足充分条件的一定满足必要条件。

（如证明一个图形是直角三角形，必要条件可以是：这个图形是三角形，充分条件可以是：这个图形是等腰RT三角形）

有这样的结论：

• 所有有这样的关系：必要条件⊆证明条件⊆充分条件
• 如果一个条件集既是必要条件又是充分条件，那么这个条件必然是证明条件。
• 我们证明必要条件就是证明满足这样的条件不一定可以构造出合法答案（找到反例）
• 我们证明充分条件就是在充分条件下，构造一种方法让其条件合法

回到题目，我们来证明上面的必要性和充分性，

• 必要性：由于上面任一子集的权值和都不足m，那么他们都至少缺一把锁不能开启，若锁的个数不足所有合法子集数把锁，那么由鸽巢原理可知，必然有两个子集缺的是同一把锁，然后如果我们把这两个子集拼起来，那么他们的权值和已经大于m了却不能打开全部的锁，与题意矛盾，故证明必要性。（可知锁至少是tot个）
• 充分性：（如果锁恰好是tot那么一定存在一种合法的分配方式让他们满足题设）假设我们将每一把锁（tot个）上都写一个居民的子集，然后令一个居民拥有除了这个居民对应的一把钥匙，然后任取一个集合和这个居民配对显然可以开启所有的锁，所有其充分性得证。
• 所以我们提出的条件是充分必要条件，所有就是证明条件，证必。

 

# include <bits/stdc++.h>
# define int long long
using namespace std;
const int MAXN=25;
int a[MAXN],t[MAXN];
int ans,n,m;
bool check()
{
    int sum=0;
    for (int i=1;i<=n;i++) if (t[i]) sum+=a[i];
    if (sum>=m) return false;
    for (int i=1;i<=n;i++) 
     if (t[i]==0&&sum+a[i]<m) return false;
    return true;  
}
void dfs(int dep)
{
    if (dep==n+1) { if (check()) ans++; return;}
    t[dep]=1;dfs(dep+1); 
    t[dep]=0;dfs(dep+1); 
}
signed main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    memset(t,0,sizeof(t));
    ans=0;
    dfs(1);
    cout<<ans<<endl;
    return 0;
}

 

 

 solution：