HGOI20181030 模拟题解

problem:给定一个序列,问你能不能通过一次交换把他弄成有序
sol:
对于0%的数据,满足数列是一个排列,然后我就打了这档分(自己瞎造的!)
对于100%的数据,显然我们先对数列进行排序然后上下匹配即可,如果数相同位置,数的大小不同有0个或2个就行否则不行
还是要仔细啊啊啊啊啊啊!


problem:给出一个图然后问你在某个地方到染料,被染的面积是多少。
sol:显然对于100%的数据情况有点多,然后我们分类讨论(我的方法贼tama烦)
首先我的草稿纸上出现这样一个东西:
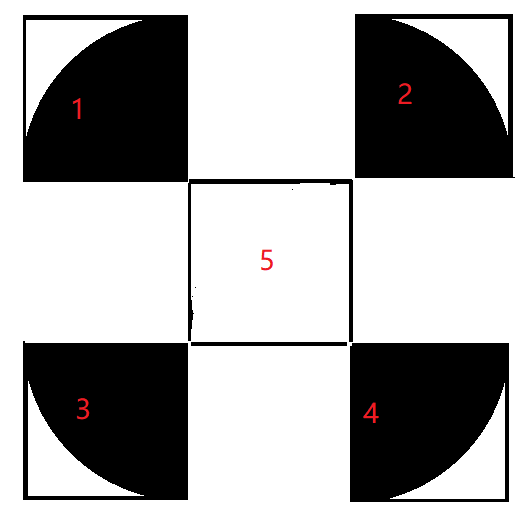
然后我就把这个图弄出来了mp数组就是存这几个图形中的一个
上面如果便利到这个点处在黑色的这边那么col=1,否则col=0
显然对于col=1,每一个格子他就是ans+=1/4π,否则ans+=1-1/4π,对于5号要特判ans+=1

对于每一个询问点我们跑4遍dfs,分别从块1-4为起点开始跑,计算面积(注意块的判重)
然后对出发情况进行分类讨论:
什么时候可以呢,我又写下了:

然后分类讨论:
- 左上出发为1:col=1,else col=0
- 左下出发为2:col=0;else col=1
- 右上出发为2:col=1;else col=0
- 右下出发为1:col=0;else col=1
- 特判:5号节点左上下右上下为5号那么col=1(其实这个倒无所谓)
然后怎么dfs呢?然后我的草稿纸上又出现的更加恶心的东西
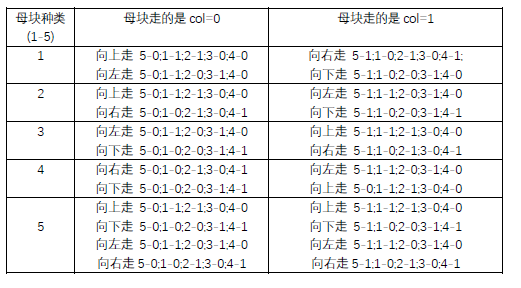
然后又是分类讨论(我都要吐了!!!)
然后写了。。大概300来行的样子吧。。也不长。。
我是码过斗地主(还有德州扑克作为第一题)的OIer!
上代码:(还打对了233333)
# include <bits/stdc++.h> #ifdef LOCAL #pragma GCC optimze(2) #endif using namespace std; const double pi=3.1415926535; const int dx[]={0,-1,0,1,0}; const int dy[]={0,0,1,0,-1}; const int MAXN=105*2; int mp[MAXN][MAXN]; bool vis[MAXN][MAXN]; int n,m; double ans; char s[MAXN]; inline int read() { int X=0,w=0; char c=0; while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar(); while ((c>='0'&&c<='9')) X=(X<<1)+(X<<3)+(c^48),c=getchar(); return w?-X:X; } inline void print(int x) { if (x<0) { putchar('-');x=-x;} if (x>9) print(x/10); putchar('0'+x%10); } inline void write(int x,int ch){ print(x);putchar(ch);} inline void writeln(int x) { print(x);putchar('\n');} void work0(int x,int y) { x*=2;y*=2; mp[x-1][y-1]=4; mp[x][y-1]=mp[x-1][y]=5; mp[x][y]=1; } void work1(int x,int y) { x*=2,y*=2; mp[x-1][y-1]=mp[x][y]=5; mp[x][y-1]=2; mp[x-1][y]=3; } bool check_wall(int x,int y) { if (mp[x][y]==2||mp[x][y]==3) return true; if (mp[x][y+1]==1||mp[x][y+1]==4) return true; if (mp[x+1][y]==1||mp[x+1][y]==4) return true; if (mp[x+1][y+1]==2||mp[x+1][y+1]==3) return true; return false; } double get(int a,int b) { if (a==5) return 1; if (b==1) return 0.25*pi; else return 1.0-0.25*pi; } void dfs(int sx,int sy,int col) { if (vis[sx][sy]) return; vis[sx][sy]=true; ans+=get(mp[sx][sy],col); for (int i=1;i<=4;i++) { int x=sx+dx[i],y=sy+dy[i]; if (x<1||x>2*n||y<1||y>2*m||vis[x][y]) continue; if (col==0) { if (mp[sx][sy]==1) { if (x==sx-1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,0);break; } } else if (x==sx&&y==sy-1) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,0);break; } } } else if (mp[sx][sy]==2) { if (x==sx-1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,0);break; } } else if (x==sx&&y==sy+1) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,1);break; } } } else if (mp[sx][sy]==3) { if (x==sx&&y==sy-1) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,0);break; } } else if (x==sx+1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,1);break; } } } else if (mp[sx][sy]==4) { if (x==sx&&y==sy+1) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,1);break; } } else if (x==sx+1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,1);break; } } } else if (mp[sx][sy]==5) { if (x==sx-1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,0);break; } } else if (x==sx&&y==sy-1) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,0);break; } } else if (x==sx+1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,1);break; } } else if(x==sx&&y==sy+1) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,1);break; } } } }else { if (mp[sx][sy]==1) { if(x==sx&&y==sy+1) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,1);break; } }else if (x==sx+1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,1);break; } } }else if (mp[sx][sy]==2) { if (x==sx&&y==sy-1) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,0);break; } } else if (x==sx+1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,1);break; } } } else if (mp[sx][sy]==3) { if (x==sx-1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,0);break; } } else if(x==sx&&y==sy+1) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,1);break; } } } else if (mp[sx][sy]==4) { if (x==sx&&y==sy-1) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,0);break; } } else if (x==sx-1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,0);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,0);break; } } } else if (mp[sx][sy]==5) { if (x==sx-1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,0);break; } } else if (x==sx&&y==sy-1) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,1);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,0);break; } } else if (x==sx+1&&y==sy) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,0);break; case 3:dfs(x,y,1);break; case 4:dfs(x,y,1);break; } } else if(x==sx&&y==sy+1) { switch (mp[x][y]) { case 5:dfs(x,y,1);break; case 1:dfs(x,y,0);break; case 2:dfs(x,y,1);break; case 3:dfs(x,y,0);break; case 4:dfs(x,y,1);break; } } } } } } int main() { #ifdef LOCAL freopen("input.in","r",stdin); #else freopen("flooding.in","r",stdin); freopen("flooding.out","w",stdout); #endif memset(mp,0,sizeof(mp)); n=read();m=read(); for (int i=1;i<=n;i++) { cin>>s;int len=strlen(s); for (int j=0;j<len;j++) if (s[j]=='0') work0(i,j+1); else work1(i,j+1); } int T=read(); int tx,ty; while (T--) { tx=read();ty=read(); if (check_wall(tx,ty)) { puts("0.0000");continue;} memset(vis,false,sizeof(vis)); ans=0; if (mp[tx][ty]==1) dfs(tx,ty,1); else if (mp[tx][ty]==4) dfs(tx,ty,0); if (mp[tx][ty+1]==2) dfs(tx,ty+1,1); else if (mp[tx][ty+1]==3) dfs(tx,ty+1,0); if (mp[tx+1][ty]==2) dfs(tx+1,ty,0); else if (mp[tx+1][ty]==3) dfs(tx+1,ty,1); if (mp[tx+1][ty+1]==1) dfs(tx+1,ty+1,0); else if (mp[tx+1][ty+1]==4) dfs(tx+1,ty+1,1); if (mp[tx][ty]==5) dfs(tx,ty,1); else if (mp[tx][ty+1]==5) dfs(tx,ty+1,1); else if (mp[tx+1][ty]==5) dfs(tx+1,ty,1); else if (mp[tx+1][ty+1]==5) dfs(tx+1,ty+1,1); printf("%.4lf\n",ans); } return 0; }

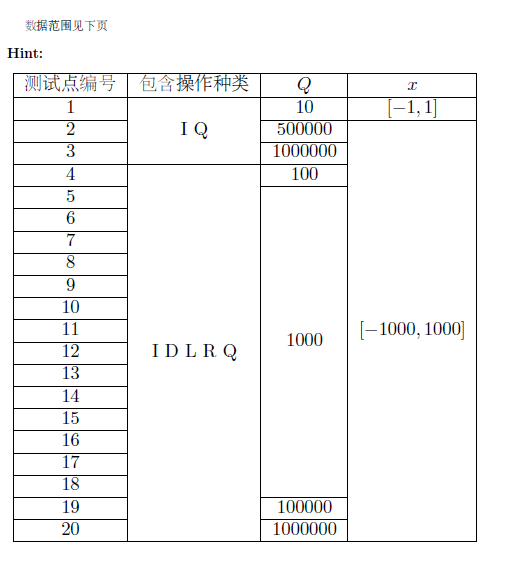
sol:显然需要注意越界的问题啊啊啊啊啊啊啊!
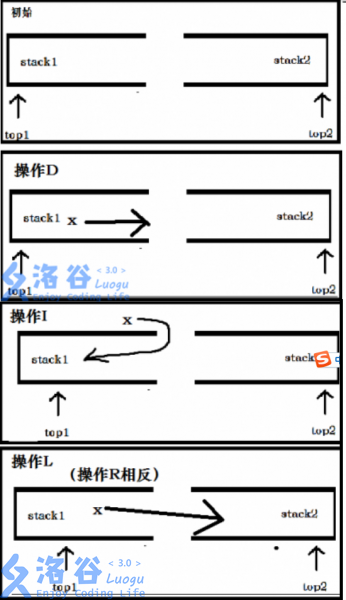
设两个手动栈St1和St2,其中保证St1都在光标左侧St2中元素被删除或者在光标的右侧,
于是我们可以维护一些删除(D)、移动(L,R)、插入(I)的操作m次操作平均复杂度基本上是O(m)的。
再维护一个现在的前缀和数组s,在每一次插入删除的时候O(1)转化(由于不影响前面的前缀和)
主要谈谈怎么样维护答案。 在每一次处理的时候ans[top1]表示前top1个元素最大前缀和是多少,只要和前缀和数组s[top1]对应取max就行
还是解释一下程序吧:
# include <bits/stdc++.h> #ifdef LOCAL #pragma GCC optimze(2) #endif using namespace std; const int MAXN=2e6+10; int st1[MAXN],st2[MAXN]; int s[MAXN],ans[MAXN]; inline int read() { int X=0,w=0; char c=0; while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar(); while ((c>='0'&&c<='9')) X=(X<<1)+(X<<3)+(c^48),c=getchar(); return w?-X:X; } inline void print(int x) { if (x<0) { putchar('-');x=-x;} if (x>9) print(x/10); putchar('0'+x%10); } inline void write(int x,int ch){ print(x);putchar(ch);} inline void writeln(int x) { print(x);putchar('\n');} int main() { ans[0]=-0x3f3f3f3f; int top1=0,top2=0,T=read(); while (T--){ char ch; cin>>ch; if(ch=='I') { int x=read(); st1[++top1]=x;//在光标前插入元素压如St1 s[top1]=x+s[top1-1]; //由于和前面不关联前缀和然后维护前缀和数组O(1) ans[top1]=max(ans[top1-1],s[top1]);//更新答案 } if(ch=='D') top1--; //出队直接弹掉就行 if(ch=='L') { if (top1!=0) { //注意判越界! int x=st1[top1--]; //把左栈元素压到右栈 st2[++top2]=x; } } if(ch=='R') { if (top2!=0) { int x=st2[top2--]; st1[++top1]=x; //把右栈元素压的左栈 s[top1]=s[top1-1]+x; //维护左边前缀和 ans[top1]=max(ans[top1-1],s[top1]); } } if(ch=='Q') { int x=read(); writeln(ans[x]);}//直接输出ans即可 } return 0; }

