普通平衡树Treap(含旋转)学习笔记

浅谈普通平衡树Treap

平衡树，Treap=Tree+heap这是一个很形象的东西

我们要维护一棵树，它满足堆的性质和二叉查找树的性质(BST)，这样的二叉树我们叫做平衡树

并且平衡树它的结构是接近于比较均衡的。

考虑Treap解决的问题：插入，删除，排名(排名为x的数，数x的排名)、前驱和后继

这里的英文函数名分别定义为insert(插入) erase(删除),rank(求数x的排名)，find(求排名是x的数)，pre(x的前驱)，nex(x的后继)

1⁰ Treap节点的定义和意义

对于一个Treap的节点我们定义如下变量size\val\cnt\key\ch[0]\ch[1]

分别解释一下他们的含义：

数的个数和数的种类是不同的概念！

size：和树链剖分中size[]的含义一样这里的含义是节点u以下含u有多少数的个数

val：储存在节点u中，相同元素的值

cnt：储存在节点u中，相同元素的数的个数

key：一个随机数在平衡树中要求父亲的key值，小于两个儿子的key值用来保证树的平衡

ch[0]：左儿子

ch[1]：右儿子

2⁰ rotate函数的解释*

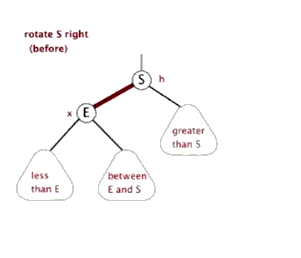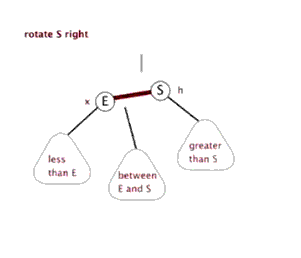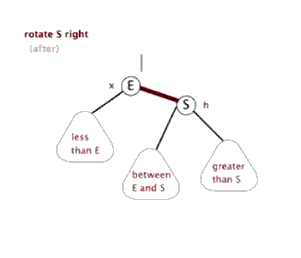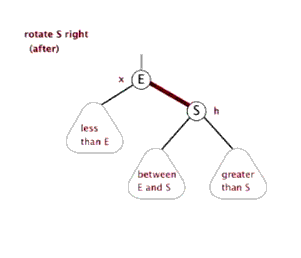
（以右旋为例）

这是原来的树：

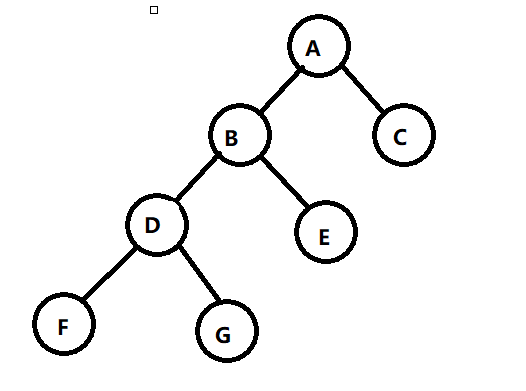
我们要把D点（是B的左儿子）右旋到根节点B

首先把D点和右节点G的边断，D和他父亲的边断。

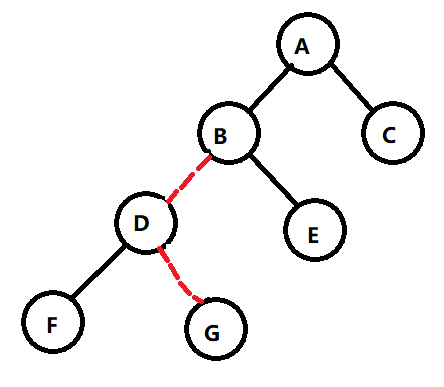
然而如果我们把D变成子树的根的话由BST的性质得D<B，所以B一定是D的右子节点。

等会！那G怎么办？

分析G的大小： B>G>D刚好可以放在B的左子树，然后把BDE这棵子树整个的连到D上刚刚好吧！

 

 其实真的比较清楚，就这么把左端点转到根节点了！

注意到我们这里是按照优先级的大小来确定转的方向从而确定出一个Heap（大根堆）的。

啊啊啊啊好容易找到两张动图GIF：

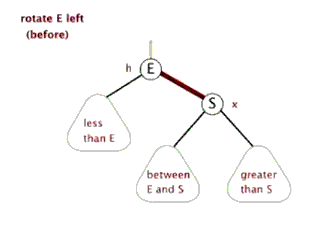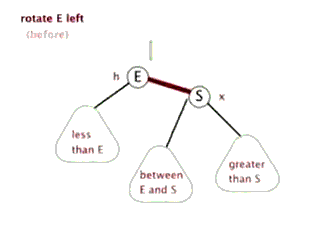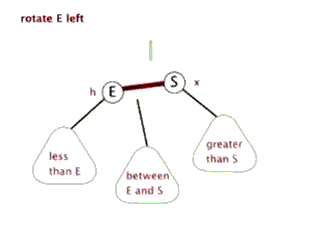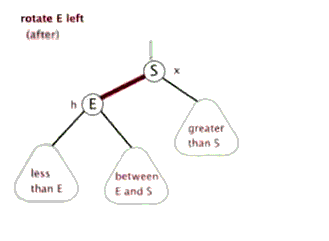
左旋：（右边儿子S上去，父亲E到左边）

右旋：（左边儿子E上去，父亲S到右边）

这样可以保证树的形态随机！

void rotate(int &x)//这是右旋
{
    int son=t[x].ch[0]; //son一直都是P 
    t[x].ch[0]=t[son].ch[1]; //Q的左节点为B
    t[son].ch[1]=x; //P的右节点是Q 
    up(x); up(x=son);//由于位置变化size和cnt都变化 
}

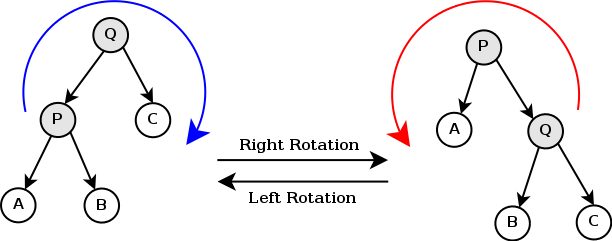
 请读者按照上图理解右旋的相关内容，并尝试写出左旋的代码：

 

void rotate(int &x)
{
    int son=t[x].ch[1];//son一直都是Q 
    t[x].ch[1]=t[son].ch[0];//P的右节点为B 
    t[son].ch[0]=x;//Q的左节点是P 
    up(x); up(x=son);//更新 
}

 

由此我们得到旋转一般写法：（d代表那个子节点（0左1右）想向上）

 

void rotate(int &x,int d)//包含左旋右旋d=1左旋(右子向上)d=0右旋(左子向上)
{
    int son=t[x].ch[d];
    t[x].ch[d]=t[son].ch[d^1];
    t[son].ch[d^1]=x;
    up(x); up(x=son);
}

3⁰其他函数略谈

A.insert

void insert(int &x,int val)//插入节点
{
    if (!x) {  //此节点为空新开一个
        x=++tot;
        t[x].size=t[x].cnt=1;
        t[x].val=val;
        t[x].key=rand();
        return;
    }
    t[x].size++; //进过一次x一定在x的子树上所以size要++
    if (t[x].val==val) { t[x].cnt++; return;} //等于就直接插入
    int d=t[x].val<val; //当前节点的val小于要求的val往大的搜
    insert(t[x].ch[d],val); //走对应的儿子
    if (t[x].key>t[t[x].ch[d]].key) rotate(x,d); //必须满足父节点的key大于两个儿子
}

B.erase

void erase(int &x,int val)
{
    if (!x) return;//节点为空跳过
    if (t[x].val==val) { //找到了
        if (t[x].cnt>1) { t[x].cnt--; t[x].size--; return;} //大于一不删点
        int d=t[ls].key>t[rs].key; //删点
        if (ls==0||rs==0) x=ls+rs; //往有孩子的一个地方走
        else rotate(x,d),erase(x,val); //先转一转把空节点放在下面，然后最终会被放在最底层
    } else t[x].size--,erase(t[x].ch[t[x].val<val],val); //经过出一定在x子树中所以x的size要--，然后往二叉查找方向搜
}

C.rank和find

int rank(int x,int val){//找val的rank值
    if (!x) return 0; //没有返回0
    if (t[x].val==val) return t[ls].size+1; //找到当前根就是x那么就是比他小的数的数目size+1（排名在他们之后）
    if (t[x].val>val) return rank(ls,val);//当前大了，那么往小的找
    return t[x].cnt+t[ls].size+rank(rs,val);  //当前小了说明左儿子的size和根节点的cnt都是比val小的要加上数的个数，然后往大的搜
}
int find(int rt,int k) //求rank=k的值是多少
{
    int x=rt; //从根开始
    while (1) {
        if (k<=t[ls].size) x=ls; //当前的k比左子树的元素个数少了那么一定往左子树搜
        else if (k>t[x].cnt+t[ls].size) k-=t[x].cnt+t[ls].size,x=rs;//如果当前的k比左子树数的个数和根节点的cnt之和还大那么就是在右子树里，减掉（t[x].cnt+t[ls].size）用新的k迭代(从另外一个根搜)
        else return t[x].val;//否则就是找到了return就行
    } 

D.pre和nex

int pre(int x,int val)
{
    if (!x) return -0x7f7f7f7f7f; //避免越界不让更新
    if (t[x].val>=val) return pre(ls,val); //等号千万别拉下
    return max(pre(rs,val),t[x].val);//以防搜不到
}
int nex(int x,int val)
{
    if (!x) return 0x7f7f7f7f7f;//避免越界不让更新
    if (t[x].val<=val) return nex(rs,val);//等号千万别拉下
    return min(nex(ls,val),t[x].val);//以防搜不到
}

4⁰模板题目

P3369 【模板】普通平衡树

题目描述

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

1. 插入x数
2. 删除x数(若有多个相同的数，因只删除一个)
3. 查询x数的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数，因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x，且最大的数)
6. 求x的后继(后继定义为大于x，且最小的数)

输入输出格式

输入格式：

第一行为n，表示操作的个数,下面n行每行有两个数opt和x，opt表示操作的序号( 1≤opt≤6 )

输出格式：

对于操作3,4,5,6每行输出一个数，表示对应答案

输入输出样例

输入样例#1： 

10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598

输出样例#1：

106465
84185
492737

输入样例#2： 

50
1 577793
1 408221
1 880861
2 408221
1 460353
1 223489
6 577713
4 2
5 889905
2 880861
1 100033
1 73956
1 22575
5 583761
6 571549
1 812645
4 3
1 643621
1 451623
6 14895
1 556691
4 1
1 225789
2 22575
1 632329
3 73956
1 316785
5 101413
4 11
5 639414
6 636353
1 272382
1 434049
2 643621
1 99617
2 577793
1 921581
1 894033
3 223489
1 767367
3 272382
1 642721
1 272033
3 632329
1 737721
1 864513
5 746457
1 877545
1 51097
1 484817

输出样例#2：

577793
460353
880861
577793
577793
100033
22575
22575
1
100033
643621
632329
643621
4
6
13
737721

说明

时空限制：1000ms,128M

1.n的数据范围： n≤100000

2.每个数的数据范围：[−10^7,10^7]

# include <bits/stdc++.h>
using namespace std;
const int MAXN=100005;
int root=0;int tot=0;
inline int read()
{
    int X=0,w=0;char c=0;
    while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar();
    while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar();
    return w?-X:X;
}
inline void po(int x){
    if (x<0) { putchar('-');x=-x;}
    if (x>9) po(x/10);
    putchar('0'+x%10);
}
inline void print(int x){ po(x);putchar('\n');}
struct Treap{ int size,val,cnt,key,ch[2];}t[MAXN];
#define ls t[x].ch[0]
#define rs t[x].ch[1]
void up(int x){t[x].size=t[x].cnt+t[ls].size+t[rs].size;}
void rotate(int &x,int d)
{
    int son=t[x].ch[d];
    t[x].ch[d]=t[son].ch[d^1];
    t[son].ch[d^1]=x;
    up(x); up(x=son);
}
void insert(int &x,int val)
{
    if (!x) { 
        x=++tot;
        t[x].size=t[x].cnt=1;
        t[x].val=val;
        t[x].key=rand();
        return;
    }
    t[x].size++;
    if (t[x].val==val) { t[x].cnt++; return;}
    int d=t[x].val<val;
    insert(t[x].ch[d],val);
    if (t[x].key>t[t[x].ch[d]].key) rotate(x,d);
}
void erase(int &x,int val)
{
    if (!x) return;
    if (t[x].val==val) {
        if (t[x].cnt>1) { t[x].cnt--; t[x].size--; return;}
        int d=t[ls].key>t[rs].key;
        if (ls==0||rs==0) x=ls+rs;
        else rotate(x,d),erase(x,val);
    } else t[x].size--,erase(t[x].ch[t[x].val<val],val);
}
inline int rank(int x,int val){
    if (!x) return 0;
    if (t[x].val==val) return t[ls].size+1;
    if (t[x].val>val) return rank(ls,val);
    return t[x].cnt+t[ls].size+rank(rs,val); 
}
int find(int rt,int k)
{
    int x=rt;
    while (1) {
        if (k<=t[ls].size) x=ls;
        else if (k>t[x].cnt+t[ls].size) k-=t[x].cnt+t[ls].size,x=rs;
        else return t[x].val;
    } 
}
inline int pre(int x,int val)
{
    if (!x) return -0x7f7f7f7f7f;
    if (t[x].val>=val) return pre(ls,val);
    return max(pre(rs,val),t[x].val);
}
int nex(int x,int val)
{
    if (!x) return 0x7f7f7f7f7f;
    if (t[x].val<=val) return nex(rs,val);
    return min(nex(ls,val),t[x].val);
}
int main()
{
    srand(time(NULL)*10007);
    int m=read(),opt,x;
    tot=0; 
    while (m--) {
        opt=read();x=read();
        switch (opt) {
            case 1:insert(root,x);break;
            case 2:erase(root,x);break;
            case 3:print(rank(root,x));break;
            case 4:print(find(root,x));break;
            case 5:print(pre(root,x));break;
            case 6:print(nex(root,x));break; 
        }
    }
    return 0;
}

5⁰注意点（容易码错的地方）

• 在全局定义root变量初始化为0
• rank函数请把return t[L].size+t[x].cnt+rank(R,val);语句放在最后不要放在中间！

6⁰STL平衡树了解下

# include <bits/stdc++.h>
# define int long long
using namespace std;
int n;
struct STL_Treap{
    vector<int>a;
    void insert(int x) { a.insert(lower_bound(a.begin(),a.end(),x),x);}
    void erase(int x)  {a.erase(lower_bound(a.begin(),a.end(),x));}
    int rank(int x) {return lower_bound(a.begin(),a.end(),x)-a.begin()+1;}
    int kth(int x){return a[x-1];}
    int pre(int x) {return *(--lower_bound(a.begin(),a.end(),x));}
    int nxt(int x){return *upper_bound(a.begin(),a.end(),x);}
}treap; 
signed main()
{
    scanf("%lld",&n);
    for (int i=1;i<=n;i++) {
        int a,b;
        scanf("%lld%lld",&a,&b);
        switch (a) {
            case 1ll:treap.insert(b);break;
            case 2ll:treap.erase(b);break;
            case 3ll:cout<<treap.rank(b)<<'\n';break;
            case 4ll:cout<<treap.kth(b)<<'\n';break;
            case 5ll:cout<<treap.pre(b)<<'\n';break;
            case 6ll:cout<<treap.nxt(b)<<'\n';break;
        }
    }
    return 0;
}