HGOI 20181027 幻象（概率DP）

• 40 pts: 考场上打了40分暴力，理论的话就是概率树，把每一个状态去去到各个带权（概率）的和就是答案

最终处理的话就是dfs出01序列0代表没有幻象，1代表出现幻象然后在每一次dfs出一段序列的时候双指针check一下更新答案

代码并不难，就是这样写的复杂度O(2ⁿ) 

code： （40pts）

# include <bits/stdc++.h>
using namespace std;
double ans;
int n,a[105];
double p1[105],p0[105];
void get()
{
    double pr=1.0;
    for (int i=1;i<=n;i++)
     if (a[i]==1) pr*=p1[i];
     else pr*=p0[i];
    int i=1; double sum=0;
    while (i<=n) {
        if (a[i]==0) { i++; continue;}
        int j=i; int res=0; 
        while (a[j]==1&&j<=n) j++,res++;
        i=j;
        sum=sum+(double) res*res;
    } 
    ans+=sum*pr;
}
void dfs(int dep)
{
    if (dep==n+1) { get(); return; }
    a[dep]=1; dfs(dep+1);
    a[dep]=0; dfs(dep+1);
}
int main()
{
    freopen("phantom.in","r",stdin);
    freopen("phantom.out","w",stdout);
    scanf("%d",&n);
    int x;
    for (int i=1;i<=n;i++) {
        scanf("%d",&x);
        p1[i]=(double) x/100.0;
        p0[i]=1.0-p1[i];
    }
    dfs(1);
    printf("%.1lf\n",ans);
    return 0;
}

• 60pts:hjc20032003考场上写了60分DP，这大概是O(n²)[前缀积]或者是O(n³)复杂度

具体做法是这样的：

令f[i]表示第i秒前幻象的期望，枚举是从j转移过来的，（这里需要注意枚举的j是断点所以从0开始枚举表示不断，否则会重复计数）

转移方程式这样的：

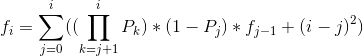
code:(60pts)

# include <bits/stdc++.h>
using namespace std;
const int MAXN=105;
double f[MAXN],p[MAXN];
int n;
int main()
{
    scanf("%d",&n); int x;
    for (int i=1;i<=n;i++) {
        scanf("%d",&x);
        p[i]=(double)x/100.0;
    } 
    f[1]=p[1];
    for (int i=2;i<=n;i++) {
        f[i]=0.0;
        for (int j=0;j<=i;j++) {
            double pr=1.0;
            for (int k=j+1;k<=i;k++) pr*=p[k];
            f[i]+=pr*(1-p[j])*(f[j-1]+(i-j)*(i-j));
        }
    }
    printf("%.1lf\n",f[n]);
    return 0;
 }

• 100pts: 状态改变一下，

记f[i]为第i秒之前期望幻象值

记g[i]为第i秒前连续期望幻象值

显然

• g[i]=(g[i-1]+1)*P[i]
• f[i]=f[i-1]+P[i]*((g[i-1]+1)²-g[i-1]²)

于是完成了O(1)转移，总复杂度O(n)

code(100 pts) 

# include <bits/stdc++.h>
using namespace std;
const int MAXN=1e6+10;
double p[MAXN],f[MAXN],g[MAXN];
int n;
double sqr(double x){ return x*x;}
int main()
{
    scanf("%d",&n);
    int x;
    for (int i=1;i<=n;i++) {
        scanf("%d",&x);
        p[i]=(double) x/100.0;
    }
    f[1]=p[1]; g[1]=p[1];
    for (int i=2;i<=n;i++) {
        f[i]=f[i-1]+p[i]*(sqr(g[i-1]+1)-sqr(g[i-1]));
        g[i]=(g[i-1]+1)*p[i];
    } 
    printf("%.1lf\n",f[n]);
    return 0;
}