整除分块 学习笔记

整除分块

HGOI20181027模拟题：

给定n,m,快速求出 FHT(n,m) % (1e9+7)的值。

 对于100%的数据： n,m <= 1,000,000,000

然后为了这个问题我们去找了整除分块的算法：

（例题） [CQOI2007]余数求和

        

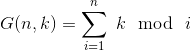
https://www.luogu.org/problemnew/show/P2261

 解析：

对于G(n,k) 化简 显然 a%b=a-[a/b]*b

 

在C++中floor(a/b)=a/b 所以我们打个表来看看k/i的规律

# include<bits/stdc++.h>
using namespace std;
int main()
{
    int n=10;
    printf("i      ");
    for (int i=1;i<=n;i++)
       printf("%d ",i);
    putchar('\n'); printf("%d/i  ",n); 
    for (int i=1;i<=n;i++) 
     printf("%d ",n/i);
    putchar('\n');
    return 0;
} 

我们发现这样的规律：n/i的值相同的总是出现在相邻位置！

 

 

在上面的式子中也就是说k/i这个东西是下取整的在一个区间内是不会变的

设[k/i]=a (这里是下取整[]): a<=k/i<a+1

然后参变分离：

得 :      i<=k/a;     i>k/(a+1)

所以在这里我们发现了对于区间i∈[L,R]其[k/i]是一个定值，当且仅当L=k/([k/i]+1)+1 ; R=k/[k/i],

所以这里的区间[l,r]可以写成： [k/(k/i+1)+1,k/(k/i) ] (这里的/是整除，和C++中/等价)

对于这里区间他们的floor(k/i)是一定的，唯一的是i在+1 +2 +3的递增所以是一个d=1的等差数列（起始值是k/i），我们只要知道左右区间就可以知道求和以后的值了

• code：(100pts)

# include <bits/stdc++.h>
# define int long long
using namespace std;
int n,k;
int calc(int n,int k) {
    int ret=0;
    for (int l=1,r;l<=n;l=r+1) {
        if (k/l!=0) r=min(k/(k/l),n);
        else r=n;
        ret+=(k/l)*(r-l+1)*(l+r)/2;
    }
    return ret;
}
int G(int n,int k) { return n*k-calc(n,k);}
signed main()
{
    scanf("%lld%lld",&n,&k);
    printf("%lld\n",G(n,k));
    return 0;
}

HGOI20181027模拟题：

给定n,m,快速求出 FHT(n,m)% (1e9+7)的值。

 对于100%的数据： n,m <= 1,000,000,000

先对式子化简：

然后就是求一部分就行了，然后就是和上面处理方法一样令G(n,k)中n=k就可以解决了

# include <bits/stdc++.h>
# define int long long
using namespace std;
const int mo=1e9+7;
int calc(int n) {
    int ret=0;
    for (int l=1,r;l<=n;l=r+1) {
        if (n/l!=0) r=min(n/(n/l),n);
        else r=n;
        ret=(ret+(n/l)*(r-l+1)*(l+r)/2%mo)%mo;
    }
    return (n*n%mo-ret%mo+mo)%mo;
}
int FHT(int n,int m){ return calc(n)*calc(m)%mo;}
signed main()
{
    int n,m; scanf("%lld%lld",&n,&m);
    printf("%lld\n",FHT(n,m));
    return 0;
}