HGOI20180831 NOIP2018模拟

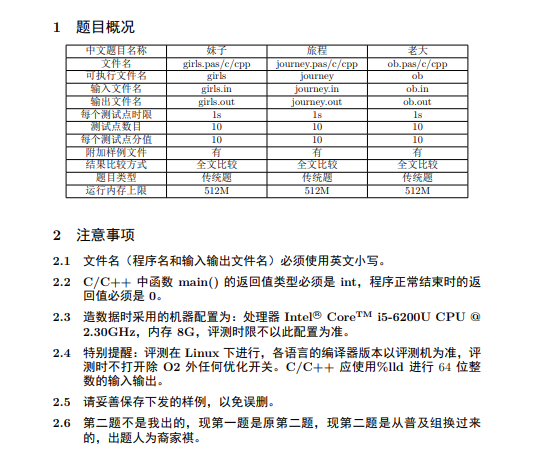
input1：

4
4 4 4 4
3 2 4 5
4 5 5 5
1 7 3 2

output1：

Yes
Yes
Yes
No

好的吧数学题QwQ考场上没人做出来qwq

就是判断两个矩形能否互相放到对方里面

后来想了想这道题怎么那么简单，判断边长不就得了吗？

虽然想到这道题是T2但还是傻到交一个可能0分的程序上去。。。（详见说明）

于是就有这么多代码。。。

• 大矩形的长大于小矩形的长，宽大于小矩形的宽，这时肯定可以放得下去；
• 大矩形的对角线小于小矩形的对角线，那么也就没有地方容下小矩形了，这时判定否；

70pts code:

# include <bits/stdc++.h>
using namespace std;
int main()
{
    freopen("girls.in","r",stdin);
    freopen("girls.out","w",stdout);
    int n; scanf("%d",&n);
    for (int i=1;i<=n;i++) {
        int a,b,c,d;
        scanf("%d%d%d%d",&a,&b,&c,&d);
        if (a>b) swap(a,b);
        if (c>d) swap(c,d);
        if (a<=c&&b<=d) printf("Yes\n");
        else if (c<=a&&d<=b) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

然后70pts 

后来发现这是有反例的qwq？

斜着放？

像这样：

 

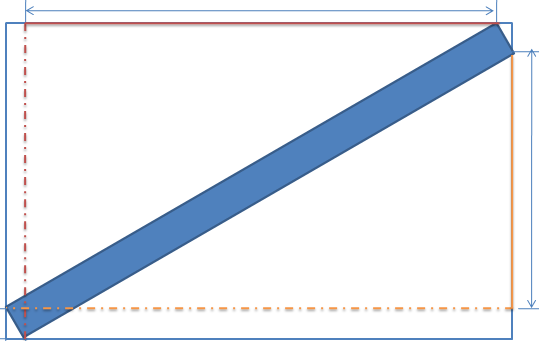
这样的话额。。好像小长方形略长一点好像是可以放下的qwq（其实也可以结合生活经验）

好的吧

 这个时候我们发现并不能直接下结论。。要推倒。。

• 当小矩形的长大于大矩形的长时，此时斜放也可能放进大矩形，所以我们进行以下计算。

具体怎么算呢？

放个图：

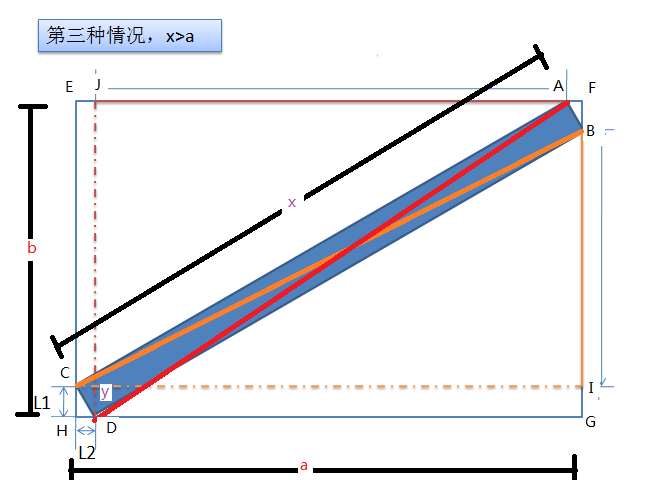
思路：求出L1，L2验证以L1，L2构成直角三角形的斜边比y大那么就行否则不行。

BC²=x²+y²又 CI²=a² 所以 BI²=BC²-CI²=x²+y²-a²

所以BI=sqrt(x²+y²-a²) 

由△ABF≌DCH（显然AAS）

BF=CH=L1 而IG=CH（矩形）

所以在GF上有 BF+BI+IG=GF 代入得 2L1+BI=EH

所以 L1=（EH-BI）/2=(b-sqrt(x²+y²-a²))/2;

同理可知 L2=（GH-AJ）/2=(a-sqrt(x²+y²-b²))/2;

若Rt△CHD中有sqrt(CD)<sqrt(L1²+L2²)即 y²<L1²+L2²

则合法否则不合法。所以有这样一个程序：

• 大矩形的长大于小矩形的长，宽大于小矩形的宽，这时肯定可以放得下去；
• 大矩形的对角线小于小矩形的对角线，那么也就没有地方容下小矩形了，这时判定否；
• 当小矩形的长大于大矩形的长时，此时斜放也可能放进大矩形，所以我们进行以下计算。如上图，假如左下角的那个小三角形，L1与L2求出第三条边大于等于小矩形的宽的话，那么小矩形就可以(碰壁)的放进去。

100pts code：

# include <bits/stdc++.h>
using namespace std;
bool fun(int x,int y,int a,int b)
//(x,y)能否放到(a,b),(长，宽)
{
    if (x<=a&&y<=b) return true;
    if (x*x+y*y>a*a+b*b) return false;
    double L1=(b-sqrt(x*x+y*y-a*a))/2.0;
    double L2=(a-sqrt(x*x+y*y-b*b))/2.0;
    if (L1*L1+L2*L2>=(double)y*y) return true;
    else return false;
}
int main()
{
    freopen("girls.in","r",stdin);
    freopen("girls.out","w",stdout);
    int T;scanf("%d",&T);
    while (T--) {
        int x,y,a,b;
        scanf("%d%d%d%d",&x,&y,&a,&b);
        if (x<y) swap(x,y);
        if (a<b) swap(a,b);
        if (fun(x,y,a,b)||fun(a,b,x,y)) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

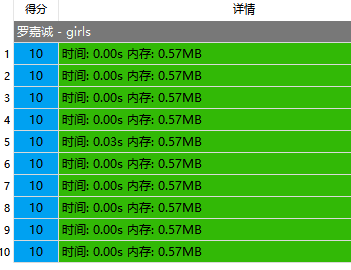
input1：

5 6
0 6 6 10 10 
2 0 7 8 6 
10 5 0 10 3 
9 5 8 0 7 
4 9 8 3 0 
1 2 3
1 4 1
2 1 3
1 4 2
1 1 2
2 4 1

output1：

6
11

题目意思：给出一幅完全图每次操作删一条边求两点最短路。（其中删边操作小于200）

要求任意两点最短路显然想到floyd最快！！！

但是要删掉一条边啊。不好办。

考场上第一想法是那道我们做过的O(n⁴)的一道加一条权为0的边求最短路

（好像是luogu2018新春模拟赛的T2）

想强制在线。。（这是显然想法好吧，是完全图、稠密图想到dijkstra好伐）

然后看到数据范围啦么小想一把暴力就过了吧，然后打了一个dijkstra堆优化好像是O(mn log n)

然后愉快的发现好像要T qwq

好的，这样以来就是想强制离线可不可以做，改删边为加边。

（反着做）我设现在要加的边为s-->t 权为w，

首先更新s--->t的最短路O(1)

那么枚举两个点u和v更新这两个点的最短距离显然有3种方法

• u--->s--->t--->v
• u--->t---->s--->v
• u--->v

由于各个点最短路我是知道的了，那么这些求值就是O(1)的了加边更新复杂度为O(n²)

有不多于200个删边操作O(n³)显然是够的，查询的话就是O(1)

这就是离线的算法。

考场上打的n<=40000的暴力dijkstra没有删去将就着看看。

# include <bits/stdc++.h>
# define INF INT_MAX/3
# define Rint register int
using namespace std;
const int MAXN=205,MAXM=100005;
struct record{
    int pre,to,w;
}a[MAXN*MAXN];
int e[MAXN][MAXN],n,m,tot=0,head[MAXN];
struct qwq{
    int c,x,y;
}q[MAXM];
int rec[MAXN][MAXN],mp[MAXN][MAXN],ans[MAXM];
inline int read()
{
    int X=0,w=0; char c=0;
    while(c<'0'||c>'9') {w|=c=='-';c=getchar();}
    while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar();
    return w?-X:X;
}
void adde(int u,int v,int w)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    a[tot].w=w;
    head[u]=tot;
}
struct ww{
    int id,lenth;
    bool operator <(const ww a) const{
        if (lenth!=a.lenth) return lenth>a.lenth;
        else return id>a.id;
    }
};
priority_queue<ww> qq;
int d[MAXN];
bool vis[MAXN];
inline void dijkstra(int s,int t)
{
    memset(vis,0,sizeof(vis));
    for (int i=1;i<=n;i++) d[i]=INF;
    d[s]=0;
    ww Node; Node.id=s;Node.lenth=0;qq.push(Node);
    while (!qq.empty()) {
        ww Node=qq.top();qq.pop();
        int u=Node.id;
        if (vis[u]) continue;
        vis[u]=true;
        for (int i=head[u];i;i=a[i].pre) {
            int v=a[i].to;
            if (d[v]-a[i].w>d[u]) {
                d[v]=d[u]+a[i].w;
                ww N;N.id=v;N.lenth=d[v];
                qq.push(N);
            }
        }
    }
    if (d[t]<INF) printf("%d\n",d[t]);
    else printf("-1\n");
}
void work1()
{
    int x,y,c;
    for (int i=1;i<=n;i++)
    for (int j=1;j<=n;j++)
    {
        scanf("%d",&x);
        if (i==j) continue;
        adde(i,j,x);e[i][j]=tot;
    }
    for (int i=1;i<=m;i++) {
        c=read();x=read();y=read();
        if (c==2) {
            dijkstra(x,y);
            continue;
        }
        a[e[x][y]].w=INF;
    }
}
int main()
{
    freopen("journey.in","r",stdin);
    freopen("journey.out","w",stdout);
    scanf("%d%d",&n,&m);
    if (m<=40000) {
        work1();
        return 0;
    }
    for (Rint i=1;i<=n;i++)
     for (Rint j=1;j<=n;j++)
      scanf("%d",&mp[i][j]),rec[i][j]=mp[i][j];
    for (Rint i=1;i<=m;i++) {
        q[i].c=read();q[i].x=read();q[i].y=read();
        if (q[i].c==1) mp[q[i].x][q[i].y]=INF;
    }
    for (Rint k=1;k<=n;k++)
     for (Rint i=1;i<=n;i++)
      for (Rint j=1;j<=n;j++)
        mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);
    for (Rint i=m;i>=1;i--) {
        if (q[i].c==2) {
              ans[++ans[0]]=mp[q[i].x][q[i].y];
              continue;
        }
        int s=q[i].x,t=q[i].y;
        mp[s][t]=min(mp[s][t],rec[s][t]);
        for (int u=1;u<=n;u++)
        for (int v=1;v<=n;v++)
         mp[u][v]=min(min(mp[u][v],mp[u][s]+mp[s][t]+mp[t][v]),mp[u][t]+mp[t][s]+mp[s][v]);
    }
    for (Rint i=ans[0];i>=1;i--)
     if (ans[i]>=INF) printf("-1");
     else printf("%d\n",ans[i]);
    return 0;
}

input1：

5
1 2
2 3
3 4
4 5

output1：

1

input2:

8
1 2
1 3
2 4
2 5
3 6
3 7
1 8

output2:

2

题目意思：是在一棵树上找到两个点使各个点到这两点的最大距离最小。

是真的不会做。。

那么就暴力本来想打LCA的结果发现floyd更快。。

就是暴力枚举那两个点，再枚举各个点到这两个点最小距离求最大值（就是按照题意模拟吧）

# include <bits/stdc++.h>
using namespace std;
const int MAXN=2005;
int mp[MAXN][MAXN];
int n;
inline int read()
{
    int X=0,w=0; char c=0;
    while(c<'0'||c>'9') {w|=c=='-';c=getchar();}
    while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar();
    return w?-X:X;
}
bool p[MAXN],vis[MAXN];
int main()
{
    freopen("ob.in","r",stdin);
    freopen("ob.out","w",stdout);
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
     for (int j=1;j<=n;j++)
      if (i!=j) mp[i][j]=INT_MAX/3;
    for (int i=1;i<=n-1;i++) {
        int u,v;
        u=read();v=read();
        mp[u][v]=1; mp[v][u]=1;
    }
    for (int k=1;k<=n;k++)
     for (int i=1;i<=n;i++)
      for (int j=1;j<=n;j++)
       if (k!=i&&i!=j&&j!=k) mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);
    int ans=INT_MAX;
    for (int t1=1;t1<=n;t1++)
     for (int t2=1;t2<=n;t2++) {
        if (t1==t2) continue;
         int Max=0;
         for (int u=1;u<=n;u++) Max=max(Max,min(mp[u][t1],mp[u][t2]));
        ans=min(ans,Max);
     }
     printf("%d\n",ans);
    return 0;
 }

话说考场上写了点奇怪的东西竟然没有T？？？

【话说如果做出来了就会update的】

• 60pts Floyd暴力模拟！！！（就是上面那种方法）
• 80pts(1) 期望树是随机的，那么默认树的直径是log级别很短，直接在直径上枚举两个点O(n log²n)-O(n³)
• 80pts(2) 考虑两个奖杯管辖范围有边界枚举一条边作为边界（u---v）u作为一棵子树，v作为一棵子树，分别求两棵树的直径求最小值O（n²）
• 100pts

显然奖杯在树的直径上（奖杯首先要将树的直径覆盖），

所以二分答案MID，表示从一个点扩展开去可以覆盖的范围

然后check的时候判断这两点扩展开去染色是否存在没有被染色的点存在，

有就是false没有就是true

　其他方法：

• 100pts （2）奖杯在直径上，二分答案后取离直径上离端点距离答案的点，遍历 check 一遍
• 100pts （3）随便提一个节点为根，二分答案，深度最深的节点一定要被照顾到，所以最深的点往上跳 答案层即可，和其距离答案以内的点都删掉，再做一次。 此法可以拓展到 k 个奖杯。
• 100pts （4）在 80 分的基础上用树形 dp，记下每个点向下前三长和向上一格后不回该子树最长的路径 长度。子树内直径是前两长的和与该子树各个子树直径取 max；子树外直径是父节点向上一格 后不回该子树最长的路径长度，前两长不进入该子树的向下最长路径这三条取前两长加起来与 父节点以上的答案取 max。

 

# include <bits/stdc++.h>
# define Rint register int
using namespace std;
const int Root=1,MAXN=200005;
struct rec{
    int pre,to;
}a[MAXN<<1];
bool col[MAXN];
int n,dep[MAXN],line[MAXN],head[MAXN],pre[MAXN],tot=0,ans;
void adde(int u,int v) //加边
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    head[u]=tot;
}
int getpts() //求出最深点并且把dep赋值为0
{
    int Max=0,P=1;
    for (int i=1;i<=n;i++)
     if (Max<dep[i]) Max=dep[i],P=i;
    memset(dep,0,sizeof(dep));
    return P;
}
void getline(int u) //求树的直径到line[]里面方便计算
{
    memset(line,0,sizeof(line));
    while (pre[u]!=-1) {
        line[++line[0]]=u;
        u=pre[u];
    }
    line[++line[0]]=u;
}
void dfs1(int u,int fat,int depth) //树的直径先一边任一点开始dfs到最深点s
{
    dep[u]=depth;
    for (Rint i=head[u];i;i=a[i].pre){
        int v=a[i].to; if (v==fat) continue;
        dfs1(v,u,depth+1);
    }
}
void dfs2(int u,int fat,int depth) //从s开始dfs到最深点t并记录每个点是从谁（pre前驱）走过来的方便搞出line[]
{
    pre[u]=fat; dep[u]=depth;
    for (Rint i=head[u];i;i=a[i].pre){
        int v=a[i].to; if (v==fat) continue;
        dfs2(v,u,depth+1);
    }
}
void draw(int u,int step,int fat) //u向外染色step步
{
    col[u]=true; //col 是true表示染色 false没染色
    if (step==0) return;
    for (Rint i=head[u];i;i=a[i].pre){
        int v=a[i].to; if (v==fat) continue;
        draw(v,step-1,u);
    }
}
bool check(int MID) //判断是否可行
{
    memset(col,false,sizeof(col));
    int Node1=line[1+MID],Node2=line[line[0]-MID]; //最深处要顾及到
    draw(Node1,MID,-1);
    draw(Node2,MID,-1);
    for (Rint i=1;i<=n;i++)
     if (!col[i]) return false;
    return true;
}
void ErFen() //二分答案
{
    int l=1,r=line[0];
    while (l<=r){
        int mid=(l+r)>>1;
        if (check(mid)) r=mid-1,ans=mid;
        else l=mid+1;
    }
}
int main()
{
    scanf("%d",&n);
    if (n<=2) { printf("0\n"); return 0; } //特判，不用走都能看到
    int u,v;
    for (Rint i=1;i<=n-1;i++)
     scanf("%d%d",&u,&v),adde(u,v),adde(v,u);
    dfs1(Root,-1,0); int s=getpts();
    memset(pre,0,sizeof(pre));
    dfs2(s,-1,0);    int t=getpts();
    getline(t);
    ErFen();
    printf("%d\n",ans);
    return 0;
}