HGOI20180823 三校联考
首测:220qwq(算差的好吧)
后来改了一个地方:300qwq(算慢的好吧)

std被踩qwq

注意:输入数据第一行忘记输入n,亲脑补
题解:
多项式除法(若最后除出的答案为1那么就是成功),对于f(x)=0的一个解x=e 单项式(x-e)必然是f(x)的一个因式
而解是[1,20]的正整数,那么暴力搜索e的值。就行
AC代码:
# include <bits/stdc++.h> # define Rint register int using namespace std; const int MAXN=100; int r[MAXN],a[MAXN],t[MAXN],n,ans[MAXN],last[MAXN]; inline bool chu(int e)//多项式除法(x-e) { memcpy(t,a,sizeof(a)); memset(r,0,sizeof(r)); for (Rint i=n;i>=1;i--) { if (t[i]==0) continue; int k=t[i]; r[i-1]=k; t[i]=0; t[i-1]=t[i-1]+k*e; } for (Rint i=0;i<=n;i++) if (t[i]!=0) return false; return true; } inline void dfs(int x,int tot) { if (tot==n) return; for (Rint i=1;i<=20;i++) { if (chu(i)) { memcpy(last,a,sizeof(a)); memcpy(a,r,sizeof(r)); ans[++ans[0]]=i; dfs(i,tot+1); memcpy(a,last,sizeof(last)); } } } int main() { freopen("equation.in","r",stdin); freopen("equation.out","w",stdout); scanf("%d",&n); for (Rint i=0;i<=n;i++) scanf("%d",&a[i]); memset(ans,0,sizeof(ans)); dfs(1,0); for (Rint i=1;i<=n;i++) printf("%d ",ans[i]); printf("\n"); return 0; }

题解:配对?马上想到二分图。 怎么建图?
加起来是质数那么就连双向边,然后跑一边匈牙利算法,答案除以二就是答案
然而这是针对数字不为0的情况,如果数字为0,那么分奇数偶数考虑
显然 (奇数)+(奇数)!=质数
(偶数)+(偶数)!=质数
左边是奇数右边是偶数,然后加起来是质数连单向边,跑匈牙利算法
这里程序用了第一种方法
# include <bits/stdc++.h> # define Rint register int using namespace std; const int MAXN=100; int n,a[MAXN],pre[MAXN],ans=0; bool mp[MAXN][MAXN],vis[MAXN]; bool prime[10001]; inline bool is_prime(int x) { if (x==1) return false; if (x==2) return true; return prime[x]; } inline bool find(int u) { for (Rint i=1;i<=n;i++) if ((!vis[i])&&(mp[u][i])) { vis[i]=true; if (pre[i]==-1||find(pre[i])){ pre[i]=u; return true; } } return false; } inline void solve() { memset(pre,-1,sizeof(pre)); for (Rint i=1;i<=n;i++){ memset(vis,false,sizeof(vis)); if (find(i)) ans++; } } inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } void getprime(int n) { memset(prime,true,sizeof(prime)); for (int i=2;i<=n;i++) { if (prime[i]==false) continue; for (int j=i+i;j<=n;j+=i) prime[j]=false; } } int main() { freopen("prime.in","r",stdin); freopen("prime.out","w",stdout); getprime(3000); scanf("%d",&n); memset(mp,false,sizeof(mp)); for (Rint i=1;i<=n;i++) a[i]=read(); for (Rint i=1;i<=n;i++) for (Rint j=1;j<=n;j++) if ((i!=j)&&(is_prime(a[i]+a[j]))) mp[i][j]=true,mp[j][i]=true; ans=0; solve(); printf("%d\n",ans/2); return 0; }


题解:和斗地主有几分胜似,暴力dfs是正解(不知道我斗地主会打几行)
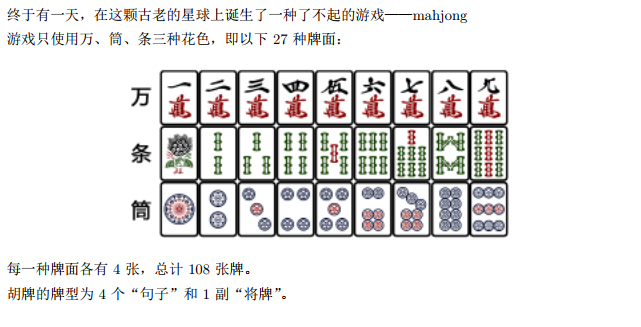
句子1 句子2 句子3 句子4 将牌
对于每个句子0表示由三张相同的牌组成,1表示3张花色相同且连续的牌组成
dfs(p1,p2,p3,p4,now)表示句子1,句子2,句子3,句子4的状态是p1,p2,p3,p4(都是0 1),now表示当前的句子是句子now
然后搜索所有状态,判断剩下的牌是不是符合条件就可以了
程序如下
# include <bits/stdc++.h> using namespace std; struct node{ char s[5]; }; struct qwq{ int hua,num; }w[15]; vector<node>v; char s[5]; int a[4][15]; bool judge() { bool flag=false; for (int i=1;i<=3;i++) for (int j=1;j<=9;j++) if (a[i][j]>0) if (a[i][j]==2) return 1 ; else return 0; } bool flag; void dfs(int p1,int p2,int p3,int p4,int now) { if (now==5) { if (judge()) { flag=true;return; } else return; } if (now==1) { if (p1==0) { for (int i=1;i<=3;i++) for (int j=1;j<=9;j++) if (a[i][j]>=3) { a[i][j]-=3; w[1].hua=w[2].hua=w[3].hua=i; w[1].num=w[2].num=w[3].num=j; dfs(p1,p2,p3,p4,now+1); a[i][j]+=3; } } else { for (int i=1;i<=3;i++) for (int j=1;j<=7;j++) if ((a[i][j]>0)&&(a[i][j+1]>0)&&(a[i][j+2]>0)) { a[i][j]--;a[i][j+1]--;a[i][j+2]--; w[1].hua=w[2].hua=w[3].hua=i; w[1].num=j;w[2].num=j+1;w[3].num=j+2; dfs(p1,p2,p3,p4,now+1); a[i][j]++;a[i][j+1]++;a[i][j+2]++; } } } else if (now==2){ if (p2==0) { for (int i=1;i<=3;i++) for (int j=1;j<=9;j++) if (a[i][j]>=3) { a[i][j]-=3; w[4].hua=w[5].hua=w[6].hua=i; w[4].num=w[5].num=w[6].num=j; dfs(p1,p2,p3,p4,now+1); a[i][j]+=3; } } else { for (int i=1;i<=3;i++) for (int j=1;j<=7;j++) if ((a[i][j]>0)&&(a[i][j+1]>0)&&(a[i][j+2]>0)) { a[i][j]--; a[i][j+1]--; a[i][j+2]--; w[4].hua=w[5].hua=w[6].hua=i; w[4].num=j;w[5].num=j+1;w[6].num=j+2; dfs(p1,p2,p3,p4,now+1); a[i][j]++;a[i][j+1]++;a[i][j+2]++; } } } else if (now==3){ if (p3==0) { for (int i=1;i<=3;i++) for (int j=1;j<=9;j++) if (a[i][j]>=3) { a[i][j]-=3; w[7].hua=w[8].hua=w[9].hua=i; w[7].num=w[8].num=w[9].num=j; dfs(p1,p2,p3,p4,now+1); a[i][j]+=3; } } else { for (int i=1;i<=3;i++) for (int j=1;j<=7;j++) if ((a[i][j]>0)&&(a[i][j+1]>0)&&(a[i][j+2]>0)) { a[i][j]--;a[i][j+1]--;a[i][j+2]--; w[7].hua=w[8].hua=w[9].hua=i; w[7].num=j;w[8].num=j+1;w[9].num=j+2; dfs(p1,p2,p3,p4,now+1); a[i][j]++;a[i][j+1]++;a[i][j+2]++; } } } else if (now==4){ if (p4==0) { for (int i=1;i<=3;i++) for (int j=1;j<=9;j++) if (a[i][j]>=3) { a[i][j]-=3; w[10].hua=w[11].hua=w[12].hua=i; w[10].num=w[11].num=w[12].num=j; dfs(p1,p2,p3,p4,now+1); a[i][j]+=3; } } else { for (int i=1;i<=3;i++) for (int j=1;j<=7;j++) if (a[i][j]>0&&a[i][j+1]>0&&a[i][j+2]>0) { a[i][j]--;a[i][j+1]--;a[i][j+2]--; w[10].hua=w[11].hua=w[12].hua=i; w[10].num=j;w[11].num=j+1;w[12].num=j+2; dfs(p1,p2,p3,p4,now+1); a[i][j]++;a[i][j+1]++;a[i][j+2]++; } } } } bool check() { for (int a=0;a<=1;a++) for (int b=0;b<=1;b++) for (int c=0;c<=1;c++) for (int d=0;d<=1;d++) { flag=false; dfs(a,b,c,d,1); if (flag) return true; } return false; } int main() { freopen("mahjong.in","r",stdin); freopen("mahjong.out","w",stdout); for (int i=1;i<=14;i++) { scanf("%s",s); node tmp; memcpy(tmp.s,s,sizeof(s)); v.push_back(tmp); } memset(a,0,sizeof(a)); for (int i=0;i<v.size();i++) { if (v[i].s[1]=='w') a[1][v[i].s[0]-'0']++; else if (v[i].s[1]=='p') a[2][v[i].s[0]-'0']++; else if (v[i].s[1]=='s') a[3][v[i].s[0]-'0']++; } int ansp=0,ansnum=0; for (int i=0;i<v.size();i++) { int ch,num; if (v[i].s[1]=='w') ch=1; else if (v[i].s[1]=='p') ch=2; else if (v[i].s[1]=='s') ch=3; num=v[i].s[0]-'0'; a[ch][num]--; int cnt=0; for (int j=1;j<=3;j++) for (int k=1;k<=9;k++) { int tt=4-a[j][k]; if (tt==0) continue; a[j][k]++; if (check()) cnt+=tt; a[j][k]--; } if (cnt>ansnum) { ansnum=cnt; ansp=i+1; } a[ch][num]++; } printf("%d %d\n",ansp,ansnum); return 0; }

