new 经典基础模板总结
NOIP-NOI-ZJOI基础模板总结
C++语言和STL库操作
重载运算符操作
/* 重载运算符 格式 如重载小于号 这里是以x递减为第一关键字比较,y递减为第二关键字比较 */ bool operator < (node a,node b){ if (a.x!=a.y) return a.x<b.x; else return a.y<b.y; }
算法类:
sort
/* sort的用法 sort(数组首位地址 ,数组末尾地址 , 比较函数) 比较函数同时可替换为重载小于号运算符 (一般采用比较函数true返回,就是保持这种趋势) 下面是一个实例,以x为第一关键字递减、以y为第二关键字递减排序 */ struct rec{ int x,y;}; bool cmp(rec a,rec b) { if (a.x!=b.x) return a.x<b.x; else return a.y<b.y; } sort(a+1,a+1+n,cmp);
swap
/* 交换两个格式相同的元素,如 int a=1,b=2; swap(a,b)完成后a=2,b=1 下面是一个清空queue的swap实现 */ void clear(queue<int> &q) { queue<int>empty; swap(q,empty); }
next_permutation
/* 求下个排列,按照字典序, next_permutation(首地址,末地址) 返回0表示已经是最后一个字典序了否则返回1 下面给出求n全排列的实现. */ # include <bits/stdc++.h> using namespace std; int main() { int n; scanf("%d",&n); int a[10]; for (int i=1;i<=n;i++) a[i]=i; do { for (int i=1;i<=n;i++) printf("%d ",a[i]); puts(""); } while (next_permutation(a+1,a+1+n)); }
max,min
/* 支持两个相同类型的元素进行比较,可以重载小于号, 取在<意义下的较小值 调用实现 */ Max=max(a,b); Min=min(a,b);
容器类:
list 双端链表
定义: list<int>lt; .begin() 返回开始 .end() 返回结束的后一个 .push_back()/.push_front() 尾部头部插入 .empty() 判断list是不是为空 .clear() 清空 .pop_back()/.pop_front() 尾部/头部删除 a.merge(b) 调用结束后b为空,a中元素包括b .insert(pos,val) pos位置插入一个或多个元素 .earse(l,r) 删除l到r所有元素 .remove(x) 删除所有元素x
bitset
定义一个bitset bitset<16> f(string("0101111001")); 按照普通计算,可以执行& | ^ << >>等操作 .count()返回1的个数 .set(p) p+1位变成1 .set(p,x) p+1位变成x .plip(p) p+1位取反 .to_ullong 转化为unsigned long long类型 .to_string 转化为string类型
stack
定义:stack<int>stt; stack 的用法 .empty() 堆栈为空则返回真 .pop() 移除栈顶元素(不会返回栈顶元素的值) .push() 在栈顶增加元素 .size() 返回栈中元素数目 .top() 返回栈顶元素
queue deque priority_queue(重载优先级)
priority_queue 优先队列 定义: /*下面两种优先队列的定义是等价的(默认)*/ priority_queue<int> q; priority_queue<int,vector<int>,less<int> > q;//大根堆 /*这一种写法与上面不等价,恰好相反*/ priority_queue<int,vectot<int>,greater<int> > q; //小根堆 重载小于号: struct rec{ int x,y; bool operator < (rec other){ if (x!=other.x) return x<other.x; else return y<other.y; } }; struct cmp{ bool operator () (rec a,b){ if (a.x!=b.x) return a.x<b.x; else return a.y<b.y; } }; priority_queue<rec,vector<rec>,cmp>q;//按照a.x和a.y为第一关键字大根堆 , 基本操作: .top() 访问堆顶元素 .push() 插入一个新元素 .pop() 删除堆顶元素 .empty() 是否为空 .size() 堆中元素个数
vector
vector的用法 定义:vector<int>a; 用法: .back(); 返回a的最后一个元素 .front(); 返回a的第一个元素 .push_back(); 插入一个元素 a[i]; 返回a的第i个元素,当且仅当a[i]存在 .erase(a.begin()+1,a.begin()+3); 删除a中第1个(从第0个算起)到第2个元素也就是说删除的元素从a.begin()+1算起(包括它)一直到a.begin()+3(不包括它) .pop_back(); 删除a向量的最后一个元素 .clear(); 清空a中的元素 .empty(); 判断a是否为空,空则返回ture,不空则返回false .swap(b); b为向量,将a中的元素和b中的元素进行整体性交换 .find(a.begin(),a.end(),10); 在a中的从a.begin()(包括它)到a.end()(不包括它)的元素中查找10,若存在返回其在向量中的位置
map
定义map<int,int>mp;//从int映射到int 用法: begin() 返回指向map头部的迭代器 clear() 删除所有元素 count() 返回指定元素出现的次数 empty() 如果map为空则返回true end() 返回指向map末尾的迭代器 erase() 删除一个元素 find() 查找一个元素 insert() 插入元素 lower_bound() 返回键值>=给定元素的第一个位置 upper_bound() 返回键值>给定元素的第一个位置 size() 返回map中元素的个数
set 和 multiset
set 和 multiset 定义set<int>st; //定义一个int 不可重复集合 定义multiset<int>st;//定义一个int 可重集 (删除的时候同时删除一样的) begin() 返回指向第一个元素的迭代器 clear() 清除所有元素 count() 返回某个值元素的个数 empty() 如果集合为空,返回true end() 返回指向最后一个元素的迭代器 erase() 删除集合中的元素 find() 返回一个指向被查找到元素的迭代器 insert() 在集合中插入元素 lower_bound() 返回指向大于(或等于)某值的第一个元素的迭代器 upper_bound() 返回大于某个值元素的迭代器 size() 集合中元素的数目
迭代器iterator的格式写法
/* 这里以遍历vector为例子,其他遍历同理 */ vector<int>::iterator it; for (it=a.begin();it!=a.end();++it) printf("%d ",*it);
基础数论模板
快速幂(乘)

int mul(int x,int n,int p) { int ans=0; while(n) { if (n&1)ans=ans+x%p; x=x+x%p; n>>=1; } return ans%p; } int fpow(int x,int n,int p) { int ans=1; while (n) { if (n&1) ans=mul(ans,x,p); x=mul(x,x,p); n>>=1; } return ans%p; }
矩阵快速幂

struct matrix{ int m[N][N]; // 矩阵乘法最后结果是A的行数,B的列数 // 乘积(i,j)位置是A第i行和B第j列对应相乘的和 matrix operator * (const matrix t) const { matrix ans; for (int i=1;i<=SIZE;i++) for (int j=1;j<=SIZE;j++) { int ret=0; for (int k=1;k<=SIZE;k++) ret=(ret+m[i][k]*t.m[k][j]%mo)%mo; ans.m[i][j]=ret; } return ans; } }; matrix mfpow(matrix x,int n) { matrix ans=x; n--; while (n) { if (n&1) ans=ans*x; x=x*x; n>>=1; } return ans; }
欧拉筛

void EouLaSha(int Lim) { memset(is_pr,true,sizeof(is_pr)); is_pr[1]=false; for (int i=2;i<=Lim;i++) { if (is_pr[i]) pr[++pr[0]]=i; for (int j=1;j<=pr[0]&&i*pr[j]<=Lim;j++) { is_pr[i*pr[j]]=false; if (i%pr[j]==0) break; } } }
埃拉托色尼筛

void Eratosthenes(int Lim) { memset(is_pr,true,sizeof(is_pr)); is_pr[1]=false; for (int i=2;i<=Lim;i++) { if (!is_pr[i]) continue; pr[++pr[0]]=i; for (int j=i+i;j<=Lim;j+=i) is_pr[j]=false; } }
米勒罗宾随机判断质数

# define int long long const int S=50; int fqow(int x,int n,int p) { int ans=1; while (n) { if (n&1) ans=ans*x%p; x=x*x%p; n>>=1; } return ans%p; } int random(int x){return 1ll*rand()*rand()%x;} bool Miller_Robbin(int x) { if (x<=1) return false; for (int i=1;i<=S;i++) { int a=random(x-1)+1; if (fqow(a,x-1,x)!=1) return false; } return true; }
gcd

# include <bits/stdc++.h> using namespace std; int gcd(int x,int y){ return y==0?x:gcd(y,x%y); } int main() { int a,b; scanf("%d%d",&a,&b); printf("%d\n",gcd(a,b)); return 0; }
exgcd

int exgcd(int a,int b,int &x,int &y) { if (b==0) { x=1;y=0; return a; } int g=exgcd(b,a%b,x,y); int t=x;x=y;y=t-a/b*x; return g; }
解不定方程ax+by=c

# include <bits/stdc++.h> # define int long long using namespace std; struct node { int x,y; bool flag; }; int exgcd(int a,int b,int &x,int &y) { if (b==0) { x=1;y=0; return a; } int g=exgcd(b,a%b,x,y); int t=x;x=y;y=t-a/b*x; return g; } node fun(int a,int b,int c) { int x,y; int g=exgcd(a,b,x,y); if (c%g!=0) return (node){-1,-1,false}; int k=c/g; return (node) {x*k,y*k,true}; } node getmin(int a,int b,int c) { int x,y; int g=exgcd(a,b,x,y); if (c%g!=0) return (node){-1,-1,false}; int k=c/g,ga=a/g,gb=b/g; x=(x*k%gb+gb)%gb; y=(c-a*x)/b; return (node){x,y,true}; } node getmax(int a,int b,int c) { int x,y; int g=exgcd(a,b,x,y); if (c%g!=0) return (node){-1,-1,false}; int k=c/g,ga=a/g,gb=b/g; y=(y*k%ga+ga)%ga; x=(c-b*y)/a; return (node){x,y,true}; } int getnum(int a,int b,int c) { int x,y; int g=exgcd(a,b,x,y); if (c%g!=0) return 0; int k=c/g,ga=a/g,gb=b/g; int xmin=(x*k%gb+gb)%gb; int ymin=(y*k%ga+ga)%ga; int xmax=(c-b*ymin)/a; return max((xmax-xmin)/gb+1,0ll); } signed main() { int a,b,c; cin>>a>>b>>c; printf("%lldx+%lldy=%lld 非负整数解有%lld对",a,b,c,getnum(a,b,c)); return 0; }
同余和同余方程(定理)
同余的定义:若a mod p = b mod p ,那么称a与b关于p同余,记作a≡b (mod p)
同余的定理:
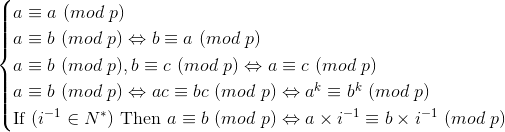
乘法逆元的定义:若ax≡1(mod p),那么称x为a在模p意义下的逆(元),记做 a-1
求逆元的方法
快速幂求逆元:
费马小定理:若p为素数,a为正整数,且a和p互质,有 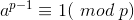
推出: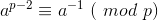

int pow(int x,int n,int p) { int ans=1; while (n) { if (n&1) ans=ans*x%p; x=x*x%p; n>>=1; } return ans%p; } int inv(int x,int m) { return pow(x,m-2,m)%m; }
扩展欧几里得求逆元
 c=1 时 等价于:
c=1 时 等价于: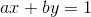
求出x的正根即可

/* 求ax=1(mod p) 就是求ax%p=1,所以ax ax=kp+1,就是ax-kp=1, 当p为质数的时候gcd(a,-p)=1,求此时x的值就是逆元 注意模到正数就行 */ int ex_gcd(int a,int b,int &x,int &y) { if (b==0) { x=1;y=0; return a; } int r=ex_gcd(b,a%b,x,y); int t=x;x=y;y=t-a/b*y; return r; } int inv(int a,int m) { int x,y; int g=ex_gcd(a,m,x,y); return (x+m)%m; }
筛选法求逆元
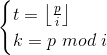
有 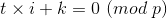
两边乘上 i-1k-1
得: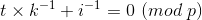
那么,
即 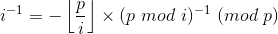

void getinv(int x,int p) { memset(inv,0,sizeof(inv)); inv[1]=1; for (int i=2;i<=x;i++) inv[i]=(long long)(p-p/i)%p*inv[p%i]%p; }
BSGS算法

# include <bits/stdc++.h> # define int long long using namespace std; map<int,int>mp; int fpow(int x,int n,int p) { int ans=1; while (n) { if (n&1) ans=ans*x%p; x=x*x%p; n>>=1; } return ans%p; } signed main() { int p,a,b; scanf("%lld%lld%lld",&p,&a,&b); int m=ceil((double)sqrt(p)); for (int j=0;j<=m;j++) mp[b*fpow(a,j,p)%p]=j; for (int i=1;i<=m;i++) if (mp.count(fpow(a,i*m,p))!=0) { printf("%lld\n",i*m-mp[fpow(a,i*m,p)]); return 0; } puts("no solution"); return 0; }
EXCRT

# include <bits/stdc++.h> # define int long long const int N=1e5+10; int n; int a[N],m[N]; using namespace std; int fmul(int x,int n,int p) { int ans=0; while (n) { if (n&1) ans=ans+x%p; x=x+x%p; n>>=1; } return ans%p; } int gcd(int a,int b) { return b==0?a:gcd(b,a%b); } int lcm(int a,int b) { int g=gcd(a,b); return a/g*b; } int exgcd(int a,int b,int &x,int &y) { if (b==0) { x=1;y=0; return a;} int g=exgcd(b,a%b,x,y); int t=x;x=y;y=t-a/b*x; return g; } int getmin(int a,int b,int c) { int x,y; c=(c%b+b)%b; int g=exgcd(a,b,x,y); if (c%g!=0) return -1; int ga=a/g,gb=b/g; int k=c/g; return (fmul(x,k,gb)%gb+gb)%gb; } int EXCRT() { int a1=a[1],m1=m[1]; a1=(a1%m1+m1)%m1; for (int i=2;i<=n;i++) { int xmin=getmin(m1,m[i],(a[i]-a1)); if (xmin==-1) return -1; a1=a1+m1*xmin; m1=lcm(m1,m[i]); a1=(a1%m1+m1)%m1; } return (a1%m1+m1)%m1; } signed main() { scanf("%lld",&n); for (int i=1;i<=n;i++) scanf("%lld%lld",&m[i],&a[i]); cout<<EXCRT()<<'\n'; return 0; }
杜教筛
组合数
对于n个数中取m个数的组合总数,有$C_{n}^{m}=(_{m}^{n})=\frac{n!}{(n-m)! \times m! }$
组合数递推(杨辉三角)

# include <bits/stdc++.h> using namespace std; const int N=1e3+10; int c[N][N],n; int main() { scanf("%d",&n); for (int i=0;i<=n;i++) c[i][0]=c[i][i]=1; for (int i=1;i<=n;i++) for (int j=1;j<=i;j++) c[i][j]=c[i-1][j]+c[i-1][j-1]; for (int i=1;i<=n;i++) { for (int j=1;j<=i;j++) printf("%d ",c[i][j]); puts(""); } return 0; }
lucas定理

# include <bits/stdc++.h> # define int long long using namespace std; const int N=2e5+10; int s[N],inv[N],n,m,p; void init(int len) { s[0]=inv[0]=inv[1]=1; for (int i=1;i<=len;i++) s[i]=s[i-1]*i%p; for (int i=2;i<=len;i++) inv[i]=(p-p/i)%p*inv[p%i]%p; for (int i=2;i<=len;i++) inv[i]=inv[i-1]*inv[i]%p; } int lucas(int n,int m,int p) { if (m>n) return 0; if (n<p&&m<p) return s[n]*inv[n-m]%p*inv[m]%p; return lucas(n%p,m%p,p)*lucas(n/p,m/p,p)%p; } signed main() { int T;scanf("%lld",&T); while (T--) { scanf("%lld%lld%lld",&n,&m,&p); init(n+m); cout<<lucas(n+m,m,p)<<'\n'; } return 0; }
二项式定理
$(x+y)^n = \sum\limits_{i=0}^{n} (^{n} _{i}) x^{n-i} y^i$
分解质因数(唯一分解定理)
对于大于1的自然数x,可以把x表示为若干个质数的乘积的形式。
即$X = P_1 ^ {a_1} \times P_2 ^{a_2} \times .... \times P_k ^ {a_k} = \prod\limits_{i=1}^{n} P_i^{a_i}$
对于$X$的正约数个数就是$\prod\limits_{i=1}^{k} (a_i+1)$
对于小于等于$10^7$的数分解质因数

# include <bits/stdc++.h> # define int long long using namespace std; const int N=1e7+10; int min_p[N],pr[N]; int a[1005],p[1005]; bool is_pr[N]; void EouLaSha(int Lim) { memset(is_pr,true,sizeof(is_pr)); is_pr[1]=false; for (int i=2;i<=Lim;i++) { if (is_pr[i]) pr[++pr[0]]=i,min_p[i]=i; for (int j=1;j<=pr[0]&&i*pr[j]<=Lim;j++) { is_pr[i*pr[j]]=false; min_p[i*pr[j]]=pr[j]; if (i%pr[j]==0) break; } } } void fun(int x) { memset(a,0,sizeof(a)); memset(p,0,sizeof(p)); p[0]=0; if (x==1){ p[0]=a[0]=1; p[1]=a[1]=1; return;} while (x!=1) { p[0]++; int u=min_p[x]; p[p[0]]=u; while (x!=1&&x%u==0) x/=u,a[p[0]]++; } a[0]=p[0]; printf("%lld = ",x); for (int i=1;i<a[0];i++) printf("(%lld^%lld)*",p[i],a[i]); printf("(%lld^%lld)\n",p[a[0]],a[a[0]]); } signed main() { EouLaSha(1e7); while (true) { int x; scanf("%lld",&x); fun(x); } return 0; }
裴蜀定理(贝祖定理)
对于$ax+by=c$有解的充要条件是$gcd(a,b)|c$,可以证明:
充分性:由exgcd可知对于$ax+by=gcd(a,b)$一定存在无数多个解,设一解为$(x_0,y_0)$,那么构造$(x_0 \times \frac{c}{gcd(a,b)},y_0 \times \frac{c}{gcd(a,b)})$一定满足题设$ax+by=c$有解。
必要性:设c不为gcd(a,b)的倍数,即$c = k \times gcd(a,b) + w$,那么同样可以通过exgcd得出条件,而若使转变成exgcd的形式,必然出现$\frac{w}{k}$为分数的情况,和解为整数不符
推广1: 对于 $\sum\limits_{i=1}^{n} a_i\times x_i = f$有解的充要条件是$gcd(a_1,a_2,...,a_n)|f$
推广2:若给定$\{a_n\}$试求出$\{b_n\}$让$\sum\limits_{i=1}^{n} a_i \times b_i $的最小正数值,必然是$gcd(a_1,a_2,...,a_n)$
高精度算法(支持负数)

# include <bits/stdc++.h> using namespace std; const int N=1e3+10; struct lint{ int num[N],len; bool op; // false:- ; true:+ void clear(){memset(num,0,sizeof(num)); len=0; op=true;} lint () { clear(); } void read() { clear(); bool w=0; char c=0; while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar(); while (c=='0') c=getchar(); while ((c>='0'&&c<='9')) num[++len]=c-'0',c=getchar(); if (w) op=false; else op=true; for (int i=1;i<=len/2;i++) swap(num[i],num[len-i+1]); } void lltolint(int x) { if (x==0) { op=true; num[++len]=0; return;} clear(); if (x<0) op=false,x=-x; while (x>0) num[++len]=x%10,x/=10; } void print() { if (!op) putchar('-'); for (int i=len;i>=1;i--) putchar(num[i]+'0'); } int cmp_abs(lint a,lint b) { if (a.len<b.len) return -1; if (a.len>b.len) return 1; for (int i=a.len;i>=1;i--) if (a.num[i]>b.num[i]) return 1; else if (a.num[i]<b.num[i]) return -1; return 0; } int cmp(lint a,lint b) { if (a.op==true&&b.op==false) return 1; if (a.op==false&&b.op==true) return -1; int p=cmp_abs(a,b); if (a.op==true&&b.op==true) return p; else return -p; } lint abs(lint a) {a.op=true; return a;} lint abs_add(lint a,lint b){ //求|a|+|b| lint ans; ans.len=max(a.len,b.len); for (int i=1;i<=ans.len;i++) { ans.num[i]+=a.num[i]+b.num[i]; ans.num[i+1]+=ans.num[i]/10; ans.num[i]%=10; } if (ans.num[ans.len+1]) ans.len++; return ans; } lint abs_cut(lint a,lint b) { //求|a|-|b|,须保证|a|>|b| a.op=true; b.op=true; if (cmp(a,b)==-1) swap(a,b); int nm=0,rs=0; lint ans; for (int i=1;i<=a.len+1;i++) { nm=a.num[i]-b.num[i]-rs;rs=0; while (nm<0) rs++,nm+=10; ans.num[i]=nm; } int i; for (i=a.len;i>=2;i--) if (ans.num[i]) break; ans.len=i; return ans; } lint operator + (lint &t){ lint a,b=t,ans; a.len=len;memcpy(a.num,num,sizeof(num));a.op=op; if (a.op&&b.op) { ans=abs_add(a,b); return ans;} if (!a.op&&!b.op) { ans=abs_add(a,b); ans.op=false; return ans; } if (a.op&&!b.op) { if (cmp(a,abs(b))==-1) { ans=abs_cut(abs(b),a);ans.op=false;return ans; } else{ ans=abs_cut(a,b); ans.op=true; return ans; } } if (!a.op&&b.op) { if (cmp(abs(a),b)==1) { ans=abs_cut(a,b); ans.op=false; return ans; } else { ans=abs_cut(b,a); ans.op=true; return ans; } } } lint operator - (lint t) { lint a,b=t,ans; a.len=len;memcpy(a.num,num,sizeof(num));a.op=op; b.op=!b.op; ans=a+b; return ans; } lint operator * (lint t) { lint a,b=t,ans; a.len=len;memcpy(a.num,num,sizeof(num));a.op=op; ans.op=!(a.op^b.op); for (int i=1;i<=a.len;i++) for (int j=1;j<=b.len;j++) ans.num[i+j-1]+=a.num[i]*b.num[j]; for (int i=1;i<=a.len+b.len;i++) { ans.num[i+1]+=ans.num[i]/10; ans.num[i]%=10; } if (ans.num[a.len+b.len]) ans.len=a.len+b.len; else ans.len=a.len+b.len-1; return ans; } lint operator / (int t) { lint a; a.len=len; if ((op&&t>0)||(!op&&t<0)) a.op=true; else a.op=false; if (t<0) t=-t; int rest=0; for (int i=len;i>=1;i--) { rest=rest*10+num[i]; a.num[i]=rest/t; rest%=t; } while (!a.num[a.len]&&a.len>1) a.len--; return a; } }r; int main() { lint a,b,c; a.read(); b.read(); c=a+b; c.print(); puts(""); c=a-b; c.print(); puts(""); c=a*b; c.print(); puts(""); c=a/3; c.print(); puts(""); return 0; }
离散化

# include <bits/stdc++.h> using namespace std; const int N=1e5+10; int n,T,a[N],tmp[N]; int GetLi(int x) { return lower_bound(tmp+1,tmp+1+T,x)-tmp; } int GetReal(int x) { return tmp[x]; } int main() { scanf("%d",&n); for (int i=1;i<=n;i++) scanf("%d",&a[i]),tmp[++tmp[0]]=a[i]; sort(tmp+1,tmp+1+tmp[0]); T=unique(tmp+1,tmp+1+tmp[0])-tmp-1; for (int i=1;i<=n;i++) { printf("%d -> %d\n",a[i],GetLi(a[i])); printf("%d <- %d\n",GetLi(a[i]),GetReal(GetLi(a[i]))); } return 0; }
概率期望
是指一个离散型的变量X,每一次出现的概率和对应结果乘积的和。
即定义式为$E(x) = \sum\limits_{i=1}^{k} p_i x_i$
性质1:多个离散变量线性组合“线性关系” $E(\sum\limits_{i=1}^n a_i x_i) = \sum\limits_{i=1}^n a_i \times E(x_i)$
性质2:多个离散变量累乘$E(\prod\limits_{i=1}^{n} x_i)=\prod\limits_{i=1}^{n} E(x_i)$
高斯消元
求解多元一次方程$a_i \times x_i + b_i = c_i $的解$\{ x_1 , x_2 , ... ,x_n\}$

# include <bits/stdc++.h> using namespace std; const int N=105; double a[N][N]; int n; bool Gauss() { for (int i=0;i<n;i++) { int r=i; for (int j=i+1;j<n;j++) if (fabs(a[j][i])>fabs(a[r][i])) r=j; if (fabs(a[r][i])<1e-5) return 0; if (r!=i) swap(a[r],a[i]); for (int j=n;j>=i;j--) { for (int k=i+1;k<n;k++) a[k][j]-=a[k][i]/a[i][i]*a[i][j]; } } for (int i=n-1;i>=0;i--) { for (int j=i+1;j<n;j++) a[i][n]-=a[j][n]*a[i][j]; a[i][n]/=a[i][i]; } return 1; } int main() { scanf("%d",&n); for (int i=0;i<n;i++) for (int j=0;j<=n;j++) scanf("%lf",&a[i][j]); if (Gauss()==false) puts("No Solution"); else for (int i=0;i<n;i++) printf("%.2lf\n",a[i][n]); return 0; }
【置换和轮换】
基础图论模板
前向星存图
思想主要是这样的,tot表示边的编号,pre表示该边(u,a[tot].to)和u相连的上一条边的编号,若没有就是0。
而head[u]表示按顺序加入边时候最后加入的一条边的编号,不断迭代更新。
遍历的时候直接从head[u]开始按照加边顺寻往前遍历。

void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; }
Floyd求最短路

# include <bits/stdc++.h> # define Rint register int using namespace std; const int MAXN=105; int mp[MAXN][MAXN]; int main() { int n,m,s; scanf("%d%d%d",&n,&m,&s); for (Rint i=1;i<=MAXN;i++) for (Rint j=1;j<=MAXN;j++) if (i!=j) mp[i][j]=INT_MAX/3; int INF=mp[1][2]; int u,v,w; for (Rint i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&w); mp[u][v]=min(w,mp[u][v]); } for (Rint k=1;k<=n;k++) for (Rint i=1;i<=n;i++) for (Rint j=1;j<=n;j++) if (k!=i&&i!=j&&j!=k) mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]); for (Rint i=1;i<=n;i++) if (mp[s][i]==INF) printf("2147483647 "); else printf("%d ",mp[s][i]); printf("\n");return 0; }
最小环
只需要在上述Floyd的基础上增加一次枚举,
枚举之前已经求出的最短路,点的编号在[1,k-1]之间的点构成的环。
事实上,一个合法的环必然是k->i->j->k
也就是说mp[k,i]+dist[i][j]+mp[j,k],因为所有的i,j,k之间的当前最短路已知最短路,所以可以转移。

# include <bits/stdc++.h> # define Rint register int using namespace std; const int MAXN=105; int mp[MAXN][MAXN],dist[MAXN][MAXN]; int main() { int n,m,s; scanf("%d%d%d",&n,&m,&s); for (Rint i=1;i<=MAXN;i++) for (Rint j=1;j<=MAXN;j++) if (i!=j) dist[i][j]=mp[i][j]=INT_MAX/3; int INF=mp[1][2]; int u,v,w; for (Rint i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&w); mp[u][v]=mp[v][u]=dist[u][v]=dist[v][u]=min(w,mp[u][v]); } int ans=INT_MAX; for (Rint k=1;k<=n;k++) { for (Rint i=1;i<=k-1;i++) for (Rint j=i+1;j<=k-1;j++) ans=min(ans,dist[i][j]+mp[k][i]+mp[j][k]); for (Rint i=1;i<=n;i++) for (Rint j=1;j<=n;j++) dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]); } printf("%d\n",ans); return 0; }
图的传递闭包
也就是给出关系图判断两个点是否连通,显然可以用类似于最短路的方法对整个图进行松弛。

# include <bits/stdc++.h> # define Rint register int using namespace std; bool mp[101][101]; int n,m; int main() { scanf("%d%d",&n,&m); memset(mp,false,sizeof(mp)); for (int i=1;i<=n;i++) mp[i][i]=true; int u,v; for (int i=1;i<=m;i++) scanf("%d%d",&u,&v),mp[u][v]=true; for (Rint k=1;k<=n;k++) for (Rint i=1;i<=n;i++) for (Rint j=1;j<=n;j++) mp[i][j]=mp[i][j]|(mp[i][k]&&mp[k][j]); for (Rint i=1;i<=n;i++) { for (Rint j=1;j<=n;j++) if (mp[i][j]) printf("Y "); else printf("N "); printf("\n"); } return 0; }
思考floyd的本质是dp
非常显然,我们设f[i][j]表示两个点之间的最短路。
枚举k进行转移f[i][j] = min(f[i][j],f[i][k] + f[k][j] )
初始值,f[i][i]=0,直接连有的边。
需要注意转移顺序,先枚举k,然后再枚举i,j这样可以求出在中转点是[1,k]的情况下全局的最短路,
就有层次,不会重复和混乱。
Spfa求单源最短路

# include <bits/stdc++.h> using namespace std; const int MAXN=100005,MAXM=2*500005; struct rec{ int pre,to,w;}a[MAXM]; int head[MAXN],n,m,INF,tot; int d[MAXN]; inline int read() { int X=0,w=0; char c=0; while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar(); while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar(); return w?-X:X; } inline void print(int x) { if (x<0) { x=-x; putchar('-');} if (x>9) print(x/10); putchar(x%10+'0'); } void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } struct node { int lenth,id;}; struct cmp{ inline bool operator () (node x,node y) { if (x.lenth>y.lenth) return true; else return false; } }; priority_queue<node,vector<node>,cmp>q; void dijkstra(int s) { memset(d,0x3f,sizeof(d)); INF=d[0]; d[s]=0; q.push((node){0,s}); while (!q.empty()) { node u=q.top();q.pop(); for (int i=head[u.id];i;i=a[i].pre){ int v=a[i].to; if (d[v]-a[i].w>d[u.id]) { d[v]=a[i].w+d[u.id]; q.push((node) {d[v],v}); } } } } int main() { int s; n=read();m=read();s=read(); int u,v,w; while (m--) { int u=read(),v=read(),w=read(); adde(u,v,w); } dijkstra(s); for (int i=1;i<=n;i++) if (d[i]!=INF) print(d[i]),putchar(' '); else print(2147483647),putchar(' '); return 0; }
dijkstra求单源最短路

# include <bits/stdc++.h> using namespace std; const int MAXN=100005,MAXM=2*500005; struct rec{ int pre,to,w;}a[MAXM]; int head[MAXN],n,m,INF,tot; int d[MAXN]; bool vis[MAXN]; inline int read() { int X=0,w=0; char c=0; while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar(); while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar(); return w?-X:X; } inline void print(int x) { if (x<0) { x=-x; putchar('-');} if (x>9) print(x/10); putchar(x%10+'0'); } void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } struct node { int lenth,id;}; struct cmp{ inline bool operator () (node x,node y) { if (x.lenth>y.lenth) return true; else return false; } }; priority_queue<node,vector<node>,cmp>q; void dijkstra(int s) { memset(vis,false,sizeof(vis)); memset(d,0x3f,sizeof(d)); INF=d[0]; d[s]=0; q.push((node){0,s}); while (!q.empty()) { node u=q.top();q.pop(); if (vis[u.id]) continue; vis[u.id]=1; for (int i=head[u.id];i;i=a[i].pre){ int v=a[i].to; if (d[v]-a[i].w>d[u.id]) { d[v]=a[i].w+d[u.id]; q.push((node) {d[v],v}); } } } } int main() { int s; n=read();m=read();s=read(); int u,v,w; while (m--) { int u=read(),v=read(),w=read(); adde(u,v,w); } dijkstra(s); for (int i=1;i<=n;i++) if (d[i]!=INF) print(d[i]),putchar(' '); else print(2147483647),putchar(' '); return 0; }
次短路
求无向图当中[s->t]的次短路(长度第2小的路径长度)
显然,可以从s跑一遍单源最短路径dist1[i]
显然,可以从t跑一遍单源最短路径dist2[i]
然后枚举每一条边[u,v],找出dist1[u]+Dist{u,v}+dist2[v]大于最短路长度的最小值即可。
如果是有向图的话,那么显然的dist2[]应该是在反图上从t为源点跑单源最短路的值。
复杂度大概是$O(n log_2 n + E)$
也可以使用A*算法+dijkstra。

# include <iostream> # include <cstdio> # include <queue> # include <algorithm> # define int long long using namespace std; const int MAXN=5005; const int MAXM=2*100005; struct A{ int pre,to,w;}a[MAXM]; struct B{ int u,v,w;}; vector<B>E; int head[MAXN],d1[MAXN],d2[MAXN],tot=0,n,m; bool vis[MAXN]; inline int read() { int X=0,w=0;char c=0; while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar(); while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar(); return w?-X:X; } inline void write(int x) { if (x<0) { putchar('-');x=-x;} if (x>9) write(x/10); putchar(x%10+'0'); } inline void writeln(int x){write(x);putchar('\n');} inline void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } struct node{ int id,val;}; struct cmp{ bool operator () (node a,node b) const{ return a.val>b.val; } }; priority_queue<node,vector<node>,cmp>q; void dijkstra(int s,int *dist) { for(int i=1;i<=n;i++) dist[i]=0x7f7f7f7f7f,vis[i]=false; dist[s]=0; node Tmp; Tmp.id=s,Tmp.val=0; q.push(Tmp); while (!q.empty()) { node u=q.top();q.pop(); if (vis[u.id]) continue; vis[u.id]=true; for (int i=head[u.id];i;i=a[i].pre) { int v=a[i].to; if (dist[v]-a[i].w>dist[u.id]) { dist[v]=a[i].w+dist[u.id]; Tmp.id=v,Tmp.val=dist[v]; q.push(Tmp); } } } } signed main() { n=read();m=read(); for (int i=1;i<=m;i++) { int u=read(),v=read(),w=read(); B Tmp1,Tmp2; Tmp1.u=u;Tmp1.v=v;Tmp1.w=w; Tmp2.u=v;Tmp2.v=u;Tmp2.w=w; E.push_back(Tmp1); E.push_back(Tmp2); adde(u,v,w); adde(v,u,w); } dijkstra(1,d1); dijkstra(n,d2); int shortest=d1[n]; int Ans=0x7f7f7f7f7f; for (int i=0;i<E.size();i++) if (d1[E[i].u]+d2[E[i].v]+E[i].w!=shortest) Ans=min(Ans,d1[E[i].u]+d2[E[i].v]+E[i].w); writeln(Ans); return 0; }
强连通分量(kosaraju、tarjan)
kosaraju算法

# include <cstdio> # include <cstring> # include <iostream> using namespace std; struct rec{ int pre,to; }; const int MAXN=1000005; int n,m,tot1=0,tot2=0; int dfn[MAXN],head1[MAXN],head2[MAXN]; bool vis[MAXN]; rec a[MAXN],b[MAXN]; int adde1(int u,int v) //正图前向星 { tot1++; a[tot1].pre=head1[u]; a[tot1].to=v; head1[u]=tot1; } int adde2(int u,int v)//反图前向星 { tot2++; b[tot2].pre=head2[u]; b[tot2].to=v; head2[u]=tot2; } int dfs1(int u) //求dfn序 { vis[u]=true; for (int i=head1[u];i!=0;i=a[i].pre) { int v=a[i].to; if (vis[v]==true) continue; dfs1(v); } dfn[++dfn[0]]=u; } int dfs2(int u) //求环 { vis[u]=true; for (int i=head2[u];i!=0;i=b[i].pre) { int v=b[i].to; if (vis[v]==true) continue; dfs2(v); } printf("%d ",u); } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); adde1(u,v); adde2(v,u);//正图A,反图B; } memset(dfn,0,sizeof(dfn)); memset(vis,false,sizeof(vis)); for (int i=1;i<=n;i++) if (vis[i]==false) dfs1(i); //得出dfn /* printf("*****************************************************\n"); printf("调试输出dfn[]: "); for (int i=1;i<=dfn[0];i++) printf("%d ",dfn[i]); for (int i=1;i<=first[0];i++) printf("%d ",first[i]); printf("\n"); printf("*****************************************************\n"); */ memset(vis,false,sizeof(vis)); int cnt=0; for (int i=dfn[0];i>0;i--) //反序搞一搞求强联通块 { if (vis[dfn[i]]==true) continue; cnt++; printf("强联通块# %d :",cnt); dfs2(dfn[i]); printf("\n"); } return 0; }
tarjan算法求强连通分量
考虑到dfs遍历一幅图是按照一些特定的顺序来遍历的。
对于深入的边指向的是比它dfs序要大的点,而有一些边指向的却是比它dfs要小的边(返祖边)
我们需要记录一个强连通分量,就只需要把这些点通过栈的方式依次弹出就可以了。
设dfn为每个节点的dfs序,low表示在以这个节点为根的搜索树上的点的返祖边指向dfn最小的点的编号。
当我们按照这些方法处理出一棵dfs树了,那么各节点的dfn或者是low的值就不会发生变化可。
当且仅当dfn[u]=low[u]说明以u为根的搜索树里面已经构成一个最大的强连通图(即强连通分量)
弹出栈中u以上的所有节点,他们必然构成一个强连通分量。
下面是伪代码:
tarjan(u) { dfn[u] = low[u] = ++dfn[0] S.push(u) 枚举 和u相连的所有边 (u,v) { if (v没有被dfs过) { tarjan(v) low[u] = min(low[u] , low[v]) } else if (v in S) low[u] = min(low[u] , dfn[v]) } if (dfn[u] = low[u]) { while (S.top() != u) 记录S.top(),S.pop(); 记录S.top(),S.pop(); 输出记录内容就是一个强连通分量,清空记录内容。 } }

# include <bits/stdc++.h> using namespace std; const int MAXN=1000005,MAXM=1000005; bool ins[MAXN]; int low[MAXN],dfn[MAXN],head[MAXN],tot=0,tt=0,n,m; struct rec{ int pre,to; }a[MAXM]; stack<int>s; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } void trajan(int u) { tt++; low[u]=dfn[u]=tt; s.push(u); ins[u]=true; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (! dfn[v]) { trajan(v); low[u]=min(low[u],low[v]); } else if (ins[v]) low[u]=min(low[u],dfn[v]); } if (dfn[u]==low[u]) { while (true) { int v=s.top();s.pop();ins[v]=false; printf("%d ",v); if (u==v) break; } printf("\n"); } } int main() { scanf("%d%d",&n,&m); int u,v; for (int i=1;i<=m;i++) scanf("%d%d",&u,&v),adde(u,v); memset(ins,false,sizeof(ins)); memset(dfn,0,sizeof(dfn)); for (int i=1;i<=n;i++) if (!dfn[i]) trajan(i); return 0; }
最小生成树

# include<bits/stdc++.h> using namespace std; const int MAXN=5005,MAXM=2000005; struct rec{ int u,v,w; }; int tot=0; rec a[MAXM]; int f[MAXN]; int n,m; bool cmp(rec x,rec y) { return x.w<y.w; } int father(int x) { if (f[x]==x) return x; f[x]=father(f[x]); return f[x]; } void kruskal() { sort(a+1,a+1+tot,cmp); for (int i=1;i<=n;i++) f[i]=i; int cnt=0,ans=0; for (int i=1;i<=m;i++){ int fx=father(a[i].u); int fy=father(a[i].v); if (fx==fy) continue; f[fx]=fy; cnt++; ans+=a[i].w; if (cnt==n-1) break; } if (cnt==n-1) printf("%d\n",ans); else printf("无解"); } int main() { scanf("%d%d",&n,&m); tot=0; for (int i=1;i<=m;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); a[++tot].u=u; a[tot].v=v; a[tot].w=w; } kruskal(); return 0; }
次小生成树
一种可行的办法是kruskal+倍增维护。
复杂度可以做到$O(m log_2 n)$
具体做法是先使用kruskal建出mst然后枚举一条不在mst中的边(u,v)
考虑(u,v)连边构成的一个基环树上唯一的环断一条边让它变成生成树。
显然,这条边必须在这个环上。
由于是要最小化答案,所以断的边必须比枚举的这条边短的最少(但不能不短,由于严格)
考虑这些点边的最大值和次大值,如果最大值=枚举边权,那么使用次大值。
那么替换合法的话就是产生枚举边权-最大值的贡献,最小化贡献即可。
具体实现的话可以非常套路的维护u->lca的路径和v->lca的路径。
(数组是真的难开)

# include <bits/stdc++.h> # define int long long using namespace std; const int N=3e5+10,M=3e5+10; struct node{ int u,v,w; }; struct rec{ int pre,to,w;}a[N<<1]; vector<node>E; bool vis[N]; int ff[N],head[N],dep[N]; int st_max[N][24],T_max[N][24],g[N][24]; int n,m,tot,Min=1e18; bool cmp(node A,node B){return A.w<B.w;} int father(int x) { if (ff[x]==x) return x; return ff[x]=father(ff[x]); } void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } void dfs(int u,int fa) { for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (v==fa) continue; st_max[v][0]=a[i].w; T_max[v][0]=-1e18; g[v][0]=u; dep[v]=dep[u]+1; dfs(v,u); } } void init() { for (int i=1;i<=22;i++) for (int j=1;j<=n;j++) { g[j][i]=g[g[j][i-1]][i-1]; st_max[j][i]=max(st_max[j][i-1],st_max[g[j][i-1]][i-1]); T_max[j][i]=max(T_max[j][i-1],T_max[g[j][i-1]][i-1]); if (st_max[j][i-1]>st_max[g[j][i-1]][i-1]) T_max[j][i]=max(T_max[j][i],st_max[g[j][i-1]][i-1]); else if (st_max[j][i-1]<st_max[g[j][i-1]][i-1]) T_max[j][i]=max(T_max[j][i],st_max[j][i-1]); } } int LCA(int u,int v) { if (dep[u]<dep[v]) swap(u,v); for (int i=21;i>=0;i--) if (dep[g[u][i]]>=dep[v]) u=g[u][i]; if (u==v) return u; for (int i=21;i>=0;i--) if (g[u][i]!=g[v][i]) u=g[u][i],v=g[v][i]; return g[u][0]; } int get(int u,int v,int k) { int res=-1e18; for(int i=21;i>=0;i--) if(dep[g[u][i]]>=dep[v]) { if(k!=st_max[u][i]) res=max(res,st_max[u][i]); else res=max(res,T_max[u][i]); u=g[u][i]; } return res; } signed main() { scanf("%lld%lld",&n,&m); for (int i=1;i<=n;i++) ff[i]=i; for (int i=1;i<=m;i++) { int u,v,w; scanf("%lld%lld%lld",&u,&v,&w); E.push_back((node){u,v,w}); } memset(vis,false,sizeof(vis)); sort(E.begin(),E.end(),cmp); int ret=0,cnt=0; for (int i=0;i<E.size();++i) { int fx=father(E[i].u),fy=father(E[i].v); if (fx==fy) continue; ff[fx]=fy; ret+=E[i].w; vis[i]=true; adde(E[i].u,E[i].v,E[i].w); adde(E[i].v,E[i].u,E[i].w); cnt++; if (cnt==n-1) break; } dep[1]=1; dfs(1,0); init(); for (int i=0;i<E.size();++i) { if (vis[i]) continue; int L=LCA(E[i].u,E[i].v); int res=max(get(E[i].u,L,E[i].w),get(E[i].v,L,E[i].w)); Min=min(Min,E[i].w-res); } printf("%lld\n",ret+Min); return 0; }
树的直径
就是从任意端点出发dfs到最远,再从最远点dfs到最远的点,可以证明这两个点之间的路径就是树的一条直径。

#include <bits/stdc++.h> using namespace std; const int N=1e5+10; int n,tot; int head[N],d[N]; struct rec{ int pre,to,w; }a[N<<1]; void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } void dfs1(int u,int fa) { for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (v==fa) continue; d[v]=d[u]+a[i].w; dfs1(v,u); } } int Get_Max_Distance() { memset(d,0,sizeof(d)); dfs1(1,0); int start=1; for (int i=2;i<=n;i++) if (d[start]<d[i]) start=i; memset(d,0,sizeof(d)); dfs1(start,0); int Maxinum=1; for (int i=1;i<=n;i++) if (d[Maxinum]<d[i]) Maxinum=i; return d[Maxinum]; } int main() { scanf("%d",&n); for (int i=1;i<n;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); adde(u,v,w); adde(v,u,w); } int ans=Get_Max_Distance(); printf("%d\n",ans); return 0; }
树上hash(差分)
最小表示法
我们以 P5043 【模板】树同构([BJOI2015]树的同构) 为例
按照一定的顺序把孩子的Hash值作为字符串hash到父亲即可。
但是会造成一些混乱,所以必须把孩子的hash排序再hash , 这样可以保证同构树hash值一定。

# include<bits/stdc++.h> # define int long long # define hash HHash using namespace std; const int N=1e3+10,base=997,mo=1e9+9; struct rec{ int pre,to; }a[N<<1]; int n,tot,head[N],hash[N]; map<vector<int>,int>mp; void clear() { tot=0; memset(a,0,sizeof(a)); memset(head,0,sizeof(head)); } void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } vector<int>tmp; void gethash(int u,int fa) { hash[u]=1; vector<int>tmp; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (v==fa) continue; gethash(v,u); tmp.push_back(hash[v]); } sort(tmp.begin(),tmp.end()); for (int i=0;i<tmp.size();i++) hash[u]=(hash[u]*base+tmp[i])%mo; } signed main() { vector<int>tmp; int T; scanf("%lld",&T); for (int id=1;id<=T;id++) { clear(); scanf("%lld",&n); for (int i=1;i<=n;i++) { int t; scanf("%lld",&t); if (t==0) continue; adde(i,t); adde(t,i); } tmp.clear(); for (int i=1;i<=n;i++) { memset(hash,0,sizeof(hash)); gethash(i,0); tmp.push_back(hash[i]); } sort(tmp.begin(),tmp.end()); if (mp.count(tmp)!=0) printf("%lld\n",mp[tmp]); else printf("%lld\n",id),mp[tmp]=id; } return 0; }
树的最小支配集
在图G={V,E}中在点集合V中选取尽可能少的点V‘使得$\complement _{V} V'$ 中所有点都和 V‘ 有边相连。
Sol : 按照dfs序的倒序遍历每一个点,如果这个点不能被支配集支配,说明其父亲一定不在支配集中,则把其父亲直接加入支配集即可。

# include <cstdio> using namespace std; const int N=1e5+10; struct rec{ int pre,to; }a[N<<1]; int n,head[N],tot,dfn[N],acdfn[N],father[N]; bool select[N]; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } void dfs(int u,int fa) { dfn[u]=++dfn[0]; father[u]=fa; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (v==fa) continue; dfs(v,u); } } int main() { scanf("%d",&n); for (int i=1;i<n;i++) { int u,v; scanf("%d%d",&u,&v); adde(u,v); adde(v,u); } dfs(1,0); int ans=0; for (int i=1;i<=n;i++) acdfn[dfn[i]]=i; for (int i=n;i>=1;i--) { int u=acdfn[i]; if (select[u]) continue; ans++; select[father[u]]=1; for (int j=head[father[u]];j;j=a[j].pre) { int v=a[j].to; select[v]=1; } } printf("%d\n",ans); return 0; }
最小点覆盖
在图G={V,E}中在点集合V中选取尽可能少的点V‘使得E中所有边都和选出来的点相连。
Sol : 按照dfs序的倒序遍历每一个点,如果这个点和父亲直接连的这条边不能被已选点集V’覆盖。那么直接把父亲直接加入点集V’即可。
代码略。
最大独立集
在图G={V,E}中在点集合V中选取尽可能多的点V‘使得所有点之间没有边相连。
Sol : 按照dfs序的倒序遍历每一个点,如果这个点没有被覆盖,那么就把这个点加入到独立集当中,并且标记自己和父亲已经覆盖(显然父亲不能再被设为独立节点)
代码略
最大比例生成树
题目意思是:给出一个无向图G={V,E} 每个边上有2个值C和R分别,要求图中一棵生成树使得$ \frac{\sum\limits_{e\in T}C_e}{\sum\limits_{e\in T}R_e} $最大
可以考虑二分答案mid,然后考虑这种答案是否可能存在。
考虑对于每一条边c值都减去mid*R , 然后跑最大生成树,如果存在一种生成树使得权值为0,那么就找到mid即为合法。
我们考虑这个答案的可行性,如果这棵重新构造的图中MST >=0 那么铁定没有希望,直接往较小的地方找。
如果这棵重新构造的图中MST(最大生成树)<0 那么是可能的,即mid是合法的,至少,答案会比mid来的大,所以直接往较大的地方找。
可以证明,最终的答案mid的时候,其MST=0;这时候mid的值就是答案。

# include <bits/stdc++.h> using namespace std; const int N=1e5+10; const double eps=1e-7; struct rec{ int u,v,c,r; }; vector<rec>a,b; int f[N],n,m; void adde(int u,int v,int c,int r) { a.push_back((rec){u,v,c,r}); } int father(int x) { if (f[x]==x) return x; return f[x]=father(f[x]); } void clear() { for (int i=1;i<=n;i++) f[i]=i; a=b; } bool cmp(rec a,rec b){return a.c>b.c;} double MST() { sort(a.begin(),a.end(),cmp); int t=0; double ans=0; for (int i=0;i<a.size();++i) { int fx=father(a[i].u),fy=father(a[i].v); if (fx==fy) continue; t++; f[fx]=fy; ans+=a[i].c; } return ans; } bool check(double Mid) { clear(); for (int i=0;i<a.size();++i) a[i].c-=a[i].r*Mid; if (MST()>=0) return false; else return true; } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { int u,v,c,r; scanf("%d%d%d%d",&u,&v,&c,&r); adde(u,v,c,r); } b=a; double l=0,r=1e9; while (fabs(r-l)>=eps) { double mid=(l+r)/2; if (check(mid)) r=mid; else l=mid; } printf("%.5lf\n",l); return 0; }
最小瓶颈生成树
指的是在一幅无向图中求出一棵生成树使得这棵树的最大边在所有生成树中最小。
如果构造出一棵这样的生成树那么就是这棵树的最小生成树。(高度符合kruskal算法)
结论: 最小瓶颈生成树不一定是最小生成树,最小生成树都是最小瓶颈生成树。
Tarjan算法(割点、割边、无向图的双联通分量、缩点)
定义dfn[x]表示图中节点x被遍历的dfs序,low[x]表示搜索树上subtree(x) 中节点通过最多一条边能够走到节点dfs序的最小值。
赋初值low[x] = dfn[x] 然后考虑从x出发的每条边(x,y) :
- 如果在搜索树上x是y的父亲节点 那么low[x] = min(low[x] , low[y])
- 否则 low[x] = min(low[x],dfn[y]) 当前子树连到外面的“返祖边”
割边的判定: (x,y)是一条割边的充要条件是 $ dfn[x] < low[y]$ (断边后,subtree(y)会变成一个独立树)

# include <bits/stdc++.h> # define inf (0x7f7f7f7f) using namespace std; const int N=1e3+10,M=N*N; struct rec{ int pre,to; }a[M<<1]; int tot=1,ans,n,m; int dfn[N],low[N],head[N],Bridge[M]; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } void clear() { tot=1; memset(dfn,0,sizeof(dfn)); memset(head,0,sizeof(head)); } void tarjan(int u,int sameEdge) { low[u]=dfn[u]=++dfn[0]; for (int i=head[u];i;i=a[i].pre) { if (i==(sameEdge^1)) continue; int v=a[i].to; if (!dfn[v]) { tarjan(v,i); low[u]=min(low[u],low[v]); if (dfn[u]<low[v]) { Bridge[++Bridge[0]]=i/2; } } else low[u]=min(low[u],dfn[v]); } } int main() { clear(); scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); adde(u,v); adde(v,u); } ans=inf; for (int i=1;i<=n;i++) if (!dfn[i]) tarjan(i,0); for (int i=1;i<=Bridge[0];i++) printf("%d ",Bridge[i]); return 0; }
割点的判定:若x不是搜索树的根节点,则x是一个割点的充要条件是$ dfn[x] \leq low[y] $ (断点后,subtree(x) 会变成一个独立树)
若x是搜索树的根节点,则x是割点的充要条件是这棵搜索树的根节点的子树个数>=2 即可。

# include <bits/stdc++.h> using namespace std; const int N=1e5+10; struct rec{ int pre,to; }a[N<<1]; int n,m,low[N],dfn[N],head[N],tot,t[N]; bool cut[N]; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } void tarjan(int u,int fa) { low[u]=dfn[u]=++dfn[0]; int cc=0; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (!dfn[v]) { tarjan(v,fa); low[u]=min(low[u],low[v]); if (dfn[u]<=low[v]&&u!=fa) cut[u]=true; if (u==fa) cc++; } else low[u]=min(low[u],dfn[v]); } if (u==fa&&cc>=2) cut[u]=true; } int main() { scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); adde(u,v); adde(v,u); } memset(dfn,0,sizeof(dfn)); for (int i=1;i<=n;i++) if (!dfn[i]) tarjan(i,i); for (int i=1;i<=n;i++) if (cut[i]) t[++t[0]]=i; printf("%d\n",t[0]); for (int i=1;i<=t[0];i++) printf("%d ",t[i]); return 0; }
边双的定义:如果在一个无向联通图的子图中没有一条割边,那么这个子图就是一个边双联通分量。
极大边双的求法:用Tarjan算法求出割边,然后将割边删除后dfs染色即可,同一种染色的点就是构成一组极大边双。

# include <bits/stdc++.h> # define inf (0x7f7f7f7f) using namespace std; const int N=1e3+10,M=N*N; struct rec{ int pre,to; }a[M<<1]; bool CutE[M<<1]; int tot=1,ans,n,m; int dfn[N],low[N],head[N]; int col[N]; vector<int>eDCC[N]; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } void clear() { tot=1; memset(dfn,0,sizeof(dfn)); memset(head,0,sizeof(head)); } void tarjan(int u,int sameEdge) { low[u]=dfn[u]=++dfn[0]; for (int i=head[u];i;i=a[i].pre) { if (i==(sameEdge^1)) continue; int v=a[i].to; if (!dfn[v]) { tarjan(v,i); low[u]=min(low[u],low[v]); if (dfn[u]<low[v]) { CutE[i]=true; CutE[i^1]=true; } } else low[u]=min(low[u],dfn[v]); } } void dfs(int u) { col[u]=col[0]; eDCC[col[u]].push_back(u); for (int i=head[u];i;i=a[i].pre) { if (CutE[i]) continue; int v=a[i].to; if (!col[v]) dfs(v); } } int main() { clear(); scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); adde(u,v); adde(v,u); } ans=inf; for (int i=1;i<=n;i++) if (!dfn[i]) tarjan(i,0); for (int i=1;i<=n;i++) if (!col[i]) ++col[0],dfs(i); for (int i=1;i<=col[0];i++){ printf("eDCC#%d : ",i); for (int j=0;j<eDCC[i].size();j++) printf("%d ",eDCC[i][j]); puts(""); } return 0; }
点双的定义:如果在一个无向联通图的子图中没有一个割点,那么这个子图就是一个点双联通分量。
极大点双的求法:在tarjan时把经过节点压入栈中,然后遍历到一条边(x,y)的时候,如果low[y] >= dfn[x] 那么栈中元素弹出到y为止加上x构成一个极大点双。

# include <bits/stdc++.h> # define inf (0x7f7f7f7f) using namespace std; const int N=1e3+10,M=N*N; struct rec{ int pre,to; }a[M<<1]; bool CutE[M<<1]; int tot=1,ans,n,m; int dfn[N],low[N],head[N]; int col[N],s[N],top; vector<int>vDCC[N]; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } void clear() { tot=1; memset(dfn,0,sizeof(dfn)); memset(head,0,sizeof(head)); } void tarjan(int u,int sameEdge) { low[u]=dfn[u]=++dfn[0]; s[++top]=u; for (int i=head[u];i;i=a[i].pre) { if (i==(sameEdge^1)) continue; int v=a[i].to; if (!dfn[v]) { tarjan(v,i); low[u]=min(low[u],low[v]); if (dfn[u]<=low[v]) { ++col[0]; int t; do { t=s[top--]; vDCC[col[0]].push_back(t); } while (t!=v); vDCC[col[0]].push_back(u); } } else low[u]=min(low[u],dfn[v]); } } int main() { clear(); scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); adde(u,v); adde(v,u); } ans=inf; for (int i=1;i<=n;i++) if (!dfn[i]) tarjan(i,0); for (int i=1;i<=col[0];i++){ printf("vDCC#%d : ",i); for (int j=0;j<vDCC[i].size();j++) printf("%d ",vDCC[i][j]); puts(""); } return 0; }
LCA(倍增LCA即可)

# include <bits/stdc++.h> using namespace std; const int MAXN=500005; struct rec{ int pre,to;}a[MAXN*2]; int n,m,s,g[MAXN][30],dep[MAXN]; int head[MAXN],tot=0; void adde(int u,int v) { a[++tot].pre=head[u]; a[tot].to=v; head[u]=tot; } void dfs(int u,int fa) { g[u][0]=fa; dep[u]=dep[fa]+1; for (int i=head[u];i;i=a[i].pre){ int v=a[i].to; if (v==fa) continue; dfs(v,u); } } void init() { dfs(s,0); for (int i=1;i<=21;i++) for (int j=1;j<=n;j++) g[j][i]=g[g[j][i-1]][i-1]; } int LCA(int u,int v) { if (dep[u]<dep[v]) swap(u,v); for (int i=21;i>=0;i--) if (dep[g[u][i]]>=dep[v]) u=g[u][i]; if (u==v) return u; for (int i=21;i>=0;i--) if (g[u][i]!=g[v][i]) u=g[u][i],v=g[v][i]; return g[u][0]; } int main() { scanf("%d%d%d",&n,&m,&s); int u,v; for (int i=1;i<n;i++) { scanf("%d%d",&u,&v); adde(u,v);adde(v,u); } init(); for (int i=1;i<=m;i++) { int u,v; scanf("%d%d",&u,&v); printf("%d\n",LCA(u,v)); } return 0; }
K短路

# include <bits/stdc++.h> using namespace std; const int N=1e5+10,M=1e6+10; struct rec1{ int id,len; }; struct rec2{ int id,len; }; struct rec3{ int pre,to,w; }a[M<<1]; struct edge{ int u,v,w; }; vector<edge>Edge; int head[N],tot,d[N]; int n,m; void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } struct cmp1 { bool operator () (rec1 a,rec1 b) { return a.len>b.len; } }; priority_queue<rec1,vector<rec1>,cmp1>q1; void dijkstra(int s) { memset(d,0x3f,sizeof(d)); d[s]=0; q1.push((rec1){s,0}); while (q1.size()) { rec1 u=q1.top();q1.pop(); for (int i=head[u.id];i;i=a[i].pre) { int v=a[i].to; if (d[v]-a[i].w>d[u.id]) { d[v]=a[i].w+d[u.id]; q1.push((rec1) {v,d[v]}); } } } } struct cmp2 { bool operator () (rec2 a,rec2 b) { return a.len+d[a.id]>b.len+d[b.id]; } }; priority_queue<rec2,vector<rec2>,cmp2>q2; int getKthDis(int s,int t,int k) { if (s==t) k++; dijkstra(t); tot=0; memset(head,0,sizeof(head)); memset(a,0,sizeof(a)); for (int i=0;i<Edge.size();i++) { adde(Edge[i].u,Edge[i].v,Edge[i].w); } q2.push((rec2){s,0}); while (q2.size()) { rec2 u=q2.top(); q2.pop(); if (u.id==t) { k--; if (k==0) return u.len; } for (int i=head[u.id];i;i=a[i].pre) { int v=a[i].to; q2.push((rec2){v,u.len+a[i].w}); } } return -1; } int main() { int s,t,k; scanf("%d%d%d%d%d",&n,&m,&s,&t,&k); for (int i=1;i<=m;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); Edge.push_back((edge){u,v,w}); adde(v,u,w); } int ans=getKthDis(s,t,k); printf("%d\n",ans); return 0; }
二分图匹配(匈牙利算法)

# include <bits/stdc++.h> using namespace std; const int N=1e3+10; int n,m,e; int mp[N][N],vis[N],pre[N]; bool find(int u) { for (int v=1;v<=m;v++) if (mp[u][v] && !vis[v]) { vis[v]=1; if (pre[v]==-1||find(pre[v])) { pre[v]=u; return 1; } } return 0; } int solve() { int ans = 0; memset(pre,-1,sizeof(pre)); for (int i=1;i<=n;i++) { memset(vis,false,sizeof(vis)); if (find(i)) ans++; } return ans; } int main() { scanf("%d%d%d",&n,&m,&e); for (int i=1;i<=e;i++) { int u,v; scanf("%d%d",&u,&v); if (u>n||v>m) continue; mp[u][v]=1; } printf("%d\n",solve()); return 0; }
网络流(最大流、最小费用最大流)

# include <bits/stdc++.h> # define inf (0x3f3f3f3f) using namespace std; const int N=1e5+10; struct rec{ int pre,to,w; }a[N<<1]; int n,m,s,t,tot=1; int head[N]; bool vis[N]; void adde(int u,int v,int w) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; head[u]=tot; } int dfs(int u,int f) { if (u==t) return f; vis[u]=1; for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (vis[v] || !a[i].w) continue; int res=0; if ((res = dfs(v,min(f,a[i].w)))>0) { a[i].w-=res; a[i^1].w+=res; return res; } } return 0; } int main() { scanf("%d%d%d%d",&n,&m,&s,&t); for (int i=1;i<=m;i++){ int u,v,w; scanf("%d%d%d",&u,&v,&w); adde(u,v,w); adde(v,u,0); } int res=0,ans=0; while (memset(vis,false,sizeof(vis)) && (res = dfs(s,inf))>0) ans+=res; printf("%d\n",ans); return 0; }

# include <bits/stdc++.h> # define inf (0x3f3f3f3f) using namespace std; const int N=5e4+10; int n,m,s,t,flow,cost,tot=1; struct rec{ int pre,to,w,f;}a[N<<1]; bool vis[N],inq[N]; int d[N],inc[N],head[N],pre[N]; void adde(int u,int v,int w,int f) { a[++tot].pre=head[u]; a[tot].to=v; a[tot].w=w; a[tot].f=f; head[u]=tot; } bool Get(int s) { queue<int>q; memset(d,0x3f,sizeof(d)); memset(inq,false,sizeof(inq)); q.push(s); inq[s]=1; d[s]=0; inc[s]=inf; while (q.size()) { int u = q.front(); inq[u]=0; q.pop(); for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (a[i].w<=0) continue; if (d[v]>d[u]+a[i].f) { d[v]=d[u]+a[i].f; inc[v]=min(inc[u],a[i].w); pre[v]=i; if (!inq[v]) inq[v]=1,q.push(v); } } } if (d[t]==inf) return false; int u=t; while (u!=s) { int i=pre[u]; a[i].w-=inc[t]; a[i^1].w+=inc[t]; u=a[i^1].to; } flow+=inc[t]; cost+=d[t]*inc[t]; return true; } int main() { scanf("%d%d%d%d",&n,&m,&s,&t); for (int i=1;i<=m;i++) { int u,v,w,f; scanf("%d%d%d%d",&u,&v,&w,&f); adde(u,v,w,f); adde(v,u,0,-f); } while (memset(vis,false,sizeof(vis)) && Get(s)); printf("%d %d\n",flow,cost); return 0; }
欧拉 (回路、路径)
欧拉路:欧拉路是指从图中任意一个点开始到图中任意一个点结束的路径,并且图中每条边通过的且只通过一次。
欧拉回路:欧拉回路是指起点和终点相同的欧拉路。
有向图判定定理:
- 每个点的入度等于出度,则存在欧拉回路(任意一点有度的点都可以作为起点)
- 除两点外,所有点入度等于出度。这两点中一点的出度比入度大,另一点的出度比入度小,则存在欧拉路。(取出度大者为起点,入度大者为终点)
无向图判定定理:
- 所有点度都是偶数,或者恰好有两个点度是奇数,则有欧拉路。若有奇数点度,则奇数点度点一定是欧拉路的起点和终点,否则可取任意一点作为起点。
差分约束系统
对于$n$个变量满足$x_i - x_j \leq c_k $的形式,求出一组解$x_1,x_2,...,x_n$
对于每一个等式,变形$x_i \leq x_j + c_k$,考虑最短路满足该性质,所以只要从$j$向$i$连一条$c_k$的有向边,设$x_1 = 0$,跑$1$的单源最短路。
得到的答案$d$数组,恰好就是一组解。注意到任意的$d_1 + t , d_2 + t, ... , d_n + t$都是一组解。
注意到此时可能有负权边,所以只要存在负权回路,那么就判定无解,否则就是有解。
时间复杂度是$O(kE)$
基础数据结构模板
二分答案
// 整数二分 while (l<=r) { int mid = (l+r)>>1; if (check(mid)) ans = mid,l = mid+1; else r = mid-1; } // 实数二分 while (fabs(r-l)>eps) { double mid=(l+r)/2.0; if (check(mid)) ans=mid,l=mid; else r=mid; }
整体二分
cdq
字典树
并查集(hjc)
线段树(正确姿势)
树状数组(max、sum、区间修改询问、二维)
分块(+整除分块)、莫队
点分治
可持久化数据结构
树链剖分LCT
平衡树Treap
树套树
基础字符串模板
字符串Hash算法
Manacher马拉车算法
KMP算法(扩展)
后缀树、后缀自动机、AC自动机



