可持久化数据结构学习笔记
/* 可持久化的迹象,我们俯身欣赏! ——《膜你抄》 */
引子
我们在生活中可能会遇到这样的问题,要是某一变化是基于某一个历史版本而来的变化。
这样处理的过程就比较困难。(然而对于暴力这个一点都不困难)
有什么是暴力算法解决不了的呢?
又有什么暴力算法是优化不了的呢?
我们分析暴力算法的复杂度(裸暴力我们就不说了)
考虑有点技术含量的暴力:我开M个数据结构维护每一时刻的版本然后在那一时刻的版本上做操作。
Hmm...复杂度是对了,但是空间呢?大概联赛给你开放整一个内存吧。(可能还不够。。。)
我们分析这样的劣势:就是把以前一样的东西重复记录的M次。
要是我们只改变有修改部分的结构就好了!!!
于是就有了可持久化数据结构:我们只记录原来数据结构中发生改变的副本,其他的留在原数据结构中。
从Trie树开始的可持久化之旅
这个首先得搞懂思想(请确保读懂上面相关知识)
在可持久化Trie树中插入一个元素的步骤一般如下:
- 设当前可持久化Trie树的根为lstrt(lastroot),插入元素以后的根为nowrt(nowroot)
- 建立一个新的节点(根)NowRoot
- 把nowrt下所有元素的指针所指信息置为lstrt中的所有指针信息(就是吧trie[nowrt][s]=trie[lstrt][s],s为字符所有可能,但是要除去当前字符信息)
- 对于当前字符信息重新维护,并新建节点new,trie[nowrt][now_char]=new(当前字符信息重新指)
- 令lstrt=trie[lstrt][now_char],nowrt=trie[nowrt][new_char] (重新准备迭代)
- 重复3-5至所有的new_char处理完毕。
这里是对于四个字符串依次插入可持久化Trie树的图,结合上述思想理解一下:
这四个字符串依次是:“abc","abd","abcd","bcd”.

这里是一个例题:P4735 最大异或和
Solution:显然需要考虑前缀xor和,记为s[i]
对于询问操作 l,r , x 就是询问一个位子p∈[l-1,r-1]使s[p] xor (x xor s[n])
如果只考虑右端点限制,那么就是直接从root[r-1] 访问进去贪心选取就行,
我们再次考虑左端点的限制,那么我们记lastest[x]表示指针所指元素位子为x时,最后面元素插入时经过这个点的最大的序号。
(如果没有元素经过这个点置为最小值-1:我们坚决不访问他)
然后询问时候考虑左端点限制是在处理下一个点去哪的位置是last值必须大于等于l-1才被认为有效点,
然后剩下的贪心(走和当前位相反或者走有元素那边)就行。
Hint:本题卡常#3和#6点建议打上O2优化、快读、还有别打那么多头文件...

# pragma G++ optimize(2) # include <cstdio> using namespace std; const int N=600010; int n,m,tot; int trie[N*24][2],lastest[N*24],root[N],s[N]; inline int max(int x,int y){return (x>y)?x:y;} inline int read() { static char c= getchar(); int a= 0; while(c < '0' || c > '9') c= getchar(); while(c >= '0' && c <= '9') a= a * 10 + c - '0', c= getchar(); return a; } void insert(int i,int dep,int lstrt,int nowrt) { if (dep<0) { lastest[nowrt]=i; return;} int c=(s[i]>>dep) & 1; if (lstrt!=0) trie[nowrt][c^1]=trie[lstrt][c^1]; trie[nowrt][c]=++tot; insert(i,dep-1,trie[lstrt][c],trie[nowrt][c]); lastest[nowrt]=max(lastest[trie[nowrt][0]],lastest[trie[nowrt][1]]); } int ask(int nowrt,int val,int dep,int mark) { if (dep<0) return s[lastest[nowrt]]^val; int c=(val>>dep) & 1; if (lastest[trie[nowrt][c^1]]>=mark) return ask(trie[nowrt][c^1],val,dep-1,mark); else return ask(trie[nowrt][c],val,dep-1,mark); } inline void write(int x) { if (x>9) write(x/10); putchar('0'+x%10); } int main() { n=read();m=read(); int t; lastest[0]=-1; root[0]=++tot; insert(0,23,0,root[0]); for (int i=1;i<=n;i++) { t=read(); s[i]=s[i-1]^t; root[i]=++tot; insert(i,23,root[i-1],root[i]); } char op[3]; for (int i=1;i<=m;i++) { scanf("%s",op); if (op[0]=='A') { int x=read(); root[++n]=++tot; s[n]=s[n-1]^x; insert(n,23,root[n-1],root[n]); } else { int l=read(),r=read(),x=read(); write(ask(root[r-1],x^s[n],23,l-1)); putchar('\n'); } } return 0; }
提高:可持久化 SegmentTree
这个题目其实就是可持久化思想的运用,我这里写了一个维护区间的max(什么都不维护感觉慎得慌)
我把它改了一下不影响题意!!!
/* 对于操作1:输入v,1,pos,val 在历史版本v中把pos位置的数改为val作为当前版本 对于操作2:输入v,2,l,在历史版本v中输出第l位置和第l位置之间的所有数的最大值,并把版本v作为当前版本 */
考虑怎么建立一棵可持久化SegmentTree,还是保留上面可持久化的思想,只维护有更改的那些线段。
其他的不做更改(直接链到对应节点就行)。
如图:
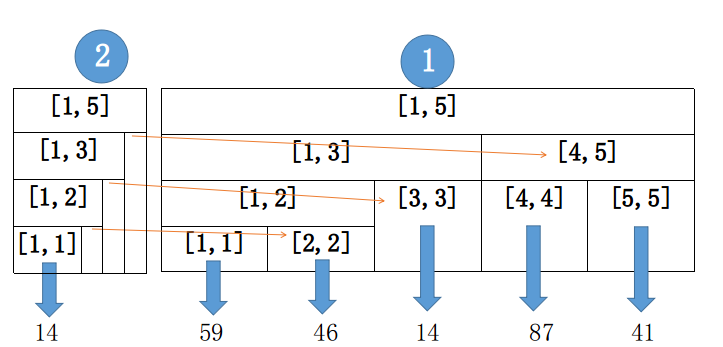
其实这个思想和前面的思想很像,但是此处和常规的线段树不同,他没有树形结构!!所以要数组模拟链表。
我们在每一个线段树的节点记录lc和rc作为左儿子节点编号和右儿子节点的编号,按照开节点的顺序编号就行。
为了节省空间,儿子的编号作为递归参数传递!
//建树 int build(int l,int r) { int p=++tot; if (l==r) { tree[p].val=a[l]; return p;} int mid=(l+r)>>1; tree[p].lc=build(l,mid); tree[p].rc=build(mid+1,r); tree[p].val=max(tree[tree[p].lc].val,tree[tree[p].rc].val); return p; }
建树的过程也不用赘述了吧。
然后是更改insert(now,l,r,x,val)操作表示当前在编号为now节点,当前区间为[l,r],然后吧x位置的值单点修改为val(即a[x]=val)
//更改 int insert(int now,int l,int r,int x,int val) { int p=++tot; tree[p]=tree[now]; if (l==r) { tree[p].val=val; return p;} int mid=(l+r)>>1; if (x<=mid) tree[p].lc=insert(tree[now].lc,l,mid,x,val); else tree[p].rc=insert(tree[now].rc,mid+1,r,x,val); tree[p].val=max(tree[tree[p].lc].val,tree[tree[p].rc].val); return p; }
注意到有个地方容易码错就是在递归insert的时候是从tree[now]出发而不是tree[p](否则不是自己到自己了吗)
但是不知道怎么过的三个点orz
接下来是query函数(这个和普通线段树大同小异)
//询问 int query(int now,int l,int r,int opl,int opr) { if (opl<=l&&r<=opr) return tree[now].val; int mid=(l+r)>>1; int val=-inf; if (opl<=mid) val=max(val,query(tree[now].lc,l,mid,opl,opr)); if (opr>mid) val=max(val,query(tree[now].rc,mid+1,r,opl,opr)); return val; }
鼓掌~~(就这么码完了)
(注意下:main函数调用子函数,and 版本编号初始为0,后面第i个询问都有基于前的新版本)

// luogu-judger-enable-o2 # include <cstdio> # define inf (0x7f7f7f7f) # define int long long using namespace std; const int N=1e6+10; int n,m,tot; int root[N*20],a[N]; struct Sem_Tree{ int lc,rc,val; }tree[N*20]; int max(int x,int y){return (x>y)?x:y;} inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } void write(int x) { if (x<0) putchar('-'),x=-x; if (x>9) write(x/10); putchar('0'+x%10); } int build(int l,int r) { int p=++tot; if (l==r) { tree[p].val=a[l]; return p;} int mid=(l+r)>>1; tree[p].lc=build(l,mid); tree[p].rc=build(mid+1,r); tree[p].val=max(tree[tree[p].lc].val,tree[tree[p].rc].val); return p; } int insert(int now,int l,int r,int x,int val) { int p=++tot; tree[p]=tree[now]; if (l==r) { tree[p].val=val; return p;} int mid=(l+r)>>1; if (x<=mid) tree[p].lc=insert(tree[now].lc,l,mid,x,val); else tree[p].rc=insert(tree[now].rc,mid+1,r,x,val); tree[p].val=max(tree[tree[p].lc].val,tree[tree[p].rc].val); return p; } int query(int now,int l,int r,int opl,int opr) { if (opl<=l&&r<=opr) return tree[now].val; int mid=(l+r)>>1; int val=-inf; if (opl<=mid) val=max(val,query(tree[now].lc,l,mid,opl,opr)); if (opr>mid) val=max(val,query(tree[now].rc,mid+1,r,opl,opr)); return val; } signed main() { n=read();m=read(); for (int i=1;i<=n;i++) a[i]=read(); root[0]=build(1,n); for (int i=1;i<=m;i++){ int id=read(),op=read(); if (op==1) { int pos=read(),v=read(); root[i]=insert(root[id],1,n,pos,v); } else { int pos=read(); int ans=query(root[id],1,n,pos,pos); root[i]=root[id]; write(ans);putchar('\n'); } } return 0; }
虽然上面的可持久化Segment确实可以解决这个问题但是,杀鸡焉用牛刀?
这里是一个裸的可持久化数组的写法(以后会衍生出类似于可持久化并查集等数据结构!)

# include <bits/stdc++.h> using namespace std; const int N=1e6+10; struct rec{ int lc,rc,val; }tree[N*20]; int n,m,root[N],tot; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } void build(int &rt,int l,int r) { rt=++tot; if (l==r) { tree[rt].val=read(); return;} int mid=(l+r)>>1; build(tree[rt].lc,l,mid); build(tree[rt].rc,mid+1,r); } int query(int rt,int l,int r,int pos) { if (l==r) return tree[rt].val; int mid=(l+r)>>1; if (pos<=mid) return query(tree[rt].lc,l,mid,pos); else return query(tree[rt].rc,mid+1,r,pos); } void update(int last,int &rt,int l,int r,int pos,int opx) { rt=++tot; tree[rt]=tree[last]; if (l==r) { tree[rt].val=opx; return;} int mid=(l+r)>>1; if (pos<=mid) update(tree[last].lc,tree[rt].lc,l,mid,pos,opx); else update(tree[last].rc,tree[rt].rc,mid+1,r,pos,opx); } int main() { n=read();m=read(); build(root[0],1,n); for (int i=1;i<=m;i++) { int id=read(),op=read(),loc=read(); if (op==1) { int val=read(); update(root[id],root[i],1,n,loc,val); } else { int ans=query(root[id],1,n,loc); root[i]=root[id]; printf("%d\n",ans); } } return 0; }
后面还有第二个稍微难一点的例题(静态区间第K小数)
不考虑l和r的限制,用线段树维护[L,R]有多少数已经被插入了,
那么我们就可以用线段树对值域的二分代替两个二分答案了。
首先吧原数组离散化,并记录离散化以后数u对应原来的哪一个整数(C++ STL)
对于离散化以后的值域[1,T]建立一棵可持久化线段树(主席树),
对于每一个原来的数a[i],把它离散化后的值d[i]加入主席树,这样我们就可以用主席树维护出前i个数有多少数(离散化后)落在值域[L,R]上了。
这对于我们后面的处理是有帮助的!
考虑我们建树的格式是一样的,若考虑opl,opr的限制,在每一个节点上若是在区间opl,opr上的数的个数那么就是这个节点中以opl-1为根的线段树该节点的个数减去以opr为根的线段树该节点的个数,这个东西就是[opl,opr]中在值域[L,R](该节点值域)中塞入元素的个数。
大概就做完了,先给出query函数
//p是后面那个节点(从root[opr]开始),q是前面那个节点(从root[opl-1])开始 //当前点的值域是[l,r],求区间k小数 int query(int p,int q,int l,int r,int k) { if (l==r) return l; int mid=(l+r)>>1; int ret=tree[tree[p].lc].val-tree[tree[q].lc].val; if (k<=ret) return query(tree[p].lc,tree[q].lc,l,mid,k); else return query(tree[p].rc,tree[q].rc,mid+1,r,k-ret); }
整个代码:Code:
要注意p,q哪个是前面的!!!

// luogu-judger-enable-o2 # include <bits/stdc++.h> using namespace std; const int N=2e5+10; map<int,int>H; int n,m,tot; int a[N],b[N],root[N]; struct Segment_Tree{ int lc,rc,val; }tree[N*20]; vector<int>tmp; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } inline void write(int x) { if (x<0) { x=-x; putchar('-');} if (x>9) write(x/10); putchar('0'+x%10); } void lisanhua(int *d,int len) { tmp.clear(); for (int i=1;i<=len;i++) tmp.push_back(d[i]); sort(tmp.begin(),tmp.end()); vector<int>::iterator it=unique(tmp.begin(),tmp.end()); for (int i=1;i<=len;i++) d[i]=lower_bound(tmp.begin(),it,d[i])-tmp.begin()+1; } int build(int l,int r) { int p=++tot; if (l==r) { tree[p].val=0; return p;} int mid=(l+r)>>1; tree[p].lc=build(l,mid); tree[p].rc=build(mid+1,r); tree[p].val=tree[tree[p].lc].val+tree[tree[p].rc].val; return p; } int insert(int now,int l,int r,int x) { int p=++tot; tree[p]=tree[now]; if (l==r) { tree[p].val++; return p;} int mid=(l+r)>>1; if (x<=mid) tree[p].lc=insert(tree[now].lc,l,mid,x); else tree[p].rc=insert(tree[now].rc,mid+1,r,x); tree[p].val=tree[tree[p].lc].val+tree[tree[p].rc].val; return p; } int query(int p,int q,int l,int r,int k) { if (l==r) return l; int mid=(l+r)>>1; int ret=tree[tree[p].lc].val-tree[tree[q].lc].val; if (k<=ret) return query(tree[p].lc,tree[q].lc,l,mid,k); else return query(tree[p].rc,tree[q].rc,mid+1,r,k-ret); } int main() { n=read();m=read(); int T=0,l,r,k; for (int i=1;i<=n;i++) b[i]=a[i]=read(); lisanhua(b,n); for (int i=1;i<=n;i++) H[b[i]]=a[i],T=max(T,b[i]); for (int i=1;i<=n;i++) root[i]=insert(root[i-1],1,T,b[i]); for (int i=1;i<=m;i++) { l=read();r=read();k=read(); int ans=query(root[r],root[l-1],1,T,k); write(H[ans]); putchar('\n'); } return 0; }
例题C: P2633 Count on a tree 【建议到bzoj2588评测】
先离散化点权,然后在每个点在值域[1,T]上建立可持久化线段树。
那么一个节点的线段树表示,从根1到该节点这条路径上在值域上塞入了多少个数!
树上主席树,对于每一个点从他的父亲基础上增加当前的点的权。
然后考虑静态在线询问,一条路径u到v,第k大权,
那么由树上差分知,(u,v)的信息=(1,u)信息+(1,v)信息-(1,lca)信息-(1,lca的父亲)信息
画个图你就明白了:
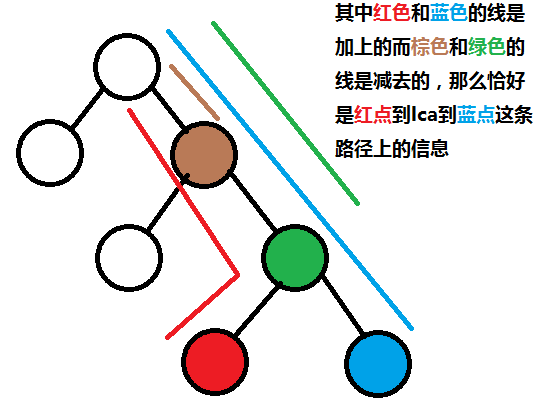
代码:Code:

# include <cstdio> # include <vector> # include <algorithm> # include <map> using namespace std; const int N=1e5+10; struct Segment_Tree{ int ls,rs,cnt; }t[N*20]; struct rec{ int pre,to; }a[N<<1]; int root[N*20],g[N][30],head[N],dep[N],val[N],b[N]; int n,m,tot,Edge,T; map<int,int>H; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } inline void write(int x) { if (x<0) x=-x,putchar('-'); if (x>9) write(x/10); putchar('0'+x%10); } void adde(int u,int v) { a[++Edge].pre=head[u]; a[Edge].to=v; head[u]=Edge; } vector<int>tmp; void lsh(int *d,int len) { tmp.clear(); for (int i=1;i<=len;i++) tmp.push_back(d[i]); sort(tmp.begin(),tmp.end()); vector<int>::iterator it=unique(tmp.begin(),tmp.end()); for (int i=1;i<=len;i++) d[i]=lower_bound(tmp.begin(),it,d[i])-tmp.begin()+1; } #define lson t[rt].ls,l,Mid #define rson t[rt].rs,Mid+1,r #define Mid ((l+r)>>1) void insert(int last,int &rt,int l,int r,int val) { rt=++tot; t[rt]=t[last]; if (l==r) {t[rt].cnt++;return;} if (val<=Mid) insert(t[last].ls,lson,val); else insert(t[last].rs,rson,val); t[rt].cnt=t[t[rt].ls].cnt+t[t[rt].rs].cnt; } int query(int ru,int rv,int rlca,int rfa,int l,int r,int k) { if (l==r) return l; int ret=t[t[ru].ls].cnt+t[t[rv].ls].cnt-t[t[rlca].ls].cnt-t[t[rfa].ls].cnt; if (k<=ret) return query(t[ru].ls,t[rv].ls,t[rlca].ls,t[rfa].ls,l,Mid,k); else return query(t[ru].rs,t[rv].rs,t[rlca].rs,t[rfa].rs,Mid+1,r,k-ret); } #undef lson #undef rson #undef Mid void dfs(int u,int fath) { g[u][0]=fath; dep[u]=dep[fath]+1; insert(root[fath],root[u],1,T,val[u]); for (int i=head[u];i;i=a[i].pre) { int v=a[i].to; if (v==fath) continue; dfs(v,u); } } int LCA(int u,int v) { if (dep[u]<dep[v]) swap(u,v); for (int i=21;i>=0;i--) if (dep[g[u][i]]>=dep[v]) u=g[u][i]; if (u==v) return u; for (int i=21;i>=0;i--) if (g[u][i]!=g[v][i]) u=g[u][i],v=g[v][i]; return g[u][0]; } int main() { //freopen("1.out","w",stdout); n=read();m=read(); T=0; for (int i=1;i<=n;i++) b[i]=val[i]=read(); lsh(b,n); for (int i=1;i<=n;i++) H[b[i]]=val[i],T=max(val[i]=b[i],T); int u,v,r,ans=0; for (int i=1;i<n;i++) { u=read(); v=read(); adde(u,v); adde(v,u); } dfs(1,0); for (int i=1;i<=21;i++) for (int j=1;j<=n;j++) g[j][i]=g[g[j][i-1]][i-1]; while (m--) { u=read()^ans;v=read();r=read(); int lca=LCA(u,v); ans=query(root[u],root[v],root[lca],root[g[lca][0]],1,T,r); ans=H[ans]; write(ans); putchar('\n'); } return 0; }
其实在算法竞赛(高端的那种)可做的题目只有数据结构题了。。。
我们考虑新鲜出炉的CTSC2018中一道混合果汁,一个显然的二分的算法呼之欲出。
但是一看它m个询问,立马否掉了,因为复杂度是O(mn log2 n)
但是思想比较重要,我们二分一个美味度D,然后吧所有美味度大于等于D的按照价格排序单减排序,
依次往后取到第k个,使前面的li之和大于等于L,又使前面的li*pi小于等于G,
这就意味这前面的这部分(1到k-1)是全取li升的,对于m个询问这种算法是TLE的。
定睛一看p的范围这么小(1e5?)其实大点没事的离散化(只不过麻烦那么一点点...)
然后就可持久化线段树维护一下p,具体的方法如下:
先把读进来的果汁种类按照d递减排序(意味着前面可以取,也可以不取)
这是由于insert是在前面的基础上操作(你访问的时候只能访问前面的,后面不行)。所以只能d递减排序。
然后对于所有在线询问,二分一个答案D,check的时候,看花掉这么多前最多可以得到几升和读入的体积比较。
具体的作法就是在query的时候能扔的扔掉类二分下去。
Code:(特别注意最后可能会取完也可能由于代价的限制取不完)

# include <cstdio> # include <algorithm> # define int long long using namespace std; const int N=1e5+10; struct Seqment_Tree{ int sum,siz,ls,rs; }t[N*20]; struct rec{ int d,p,l; }a[N]; int n,m,tot; int root[N*20]; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } inline void write(int x) { if (x>9) write(x/10); putchar('0'+x%10); } bool cmp(rec a,rec b){return a.d>b.d;} void insert(int pre,int &rt,int l,int r,int x,int v) { rt=++tot; t[rt]=t[pre]; t[rt].sum+=x*v; t[rt].siz+=v; if (l==r) return; int mid=(l+r)/2; if (x<=mid) insert(t[pre].ls,t[rt].ls,l,mid,x,v); else insert(t[pre].rs,t[rt].rs,mid+1,r,x,v); } int query(int rt,int l,int r,int x) { if (!rt) return 0; if (l==r) return min(x/l,t[rt].siz); int mid=(l+r)/2; if (t[t[rt].ls].sum>x) return query(t[rt].ls,l,mid,x); else return query(t[rt].rs,mid+1,r,x-t[t[rt].ls].sum)+t[t[rt].ls].siz; } signed main() { n=read();m=read(); int T=0; for (int i=1;i<=n;i++) a[i].d=read(),T=max(T,a[i].p=read()),a[i].l=read(); sort(a+1,a+1+n,cmp); for (int i=1;i<=n;i++) insert(root[i-1],root[i],1,T,a[i].p,a[i].l); int g,w; while (m--) { g=read();w=read(); int l=1,r=n,ans=0; while (l<=r) { int mid=(l+r)/2; if (query(root[mid],1,T,g)>=w) ans=mid,r=mid-1; else l=mid+1; } if (!ans) puts("-1"); else write(a[ans].d),putchar('\n'); } return 0; }
进阶:可持久化并查集
普通的并查集就不提了,可持久化并查集就是用个可持久化数组(线段树??)来维护这个并查集。
当然我们要考虑优化路径的方案(Hmm...就是保持这颗二叉树尽可能平均深度是log2n)
然而不能使用路径压缩。。那是因为一些非法出题人会卡爆long long,所以还是按秩合并比较稳妥。
即在合并两颗子树(根为u和v)把深度小的合到深度大的上面,并改变深度.
不妨一个个看下来这些函数。
首先两个函数分别是建可持久化数组、和可持久化数组pos位+1(方便后面按秩合并),这些是常规操作。
//建树 void build(int &rt,int l,int r) { rt=++tot; if (l==r) { tree[rt].val=l; return;} int mid=(l+r)>>1; build(tree[rt].lc,l,mid); build(tree[rt].rc,mid+1,r); } //pos位+1 void update(int rt,int l,int r,int pos) { if (l==r){ tree[rt].dep++; return ;} int mid=(l+r)>>1; if (pos<=mid) update(tree[rt].lc,l,mid,pos); else update(tree[rt].rc,mid+1,r,pos); }
接下来一个就是求pos号元素是谁(访问,这个应该是基本操作),这个也比较简单:
//返回pos号元素的根 int query(int rt,int l,int r,int pos) { if (l==r) return rt; int mid=(l+r)>>1; if (pos<=mid) return query(tree[rt].lc,l,mid,pos); else return query(tree[rt].rc,mid+1,r,pos); }
然后接下来这个就是暴力找一个节点的祖先:
//找pos号元素对应的祖先 int find(int rt,int pos) { int now=query(rt,1,n,pos); if (tree[now].val==pos) return now; return find(rt,tree[now].val); }
再来一个merge函数表示把pos这个位值连接到to这个子树上:
这主要是利用可持久话操作(之前last和now并进)
最后把节点直接父亲指向to的直接父亲,深度置为一样:
void merge(int last,int &rt,int l,int r,int pos,int to) { rt=++tot; tree[rt]=tree[last]; if (l==r) { tree[rt].val=to; tree[rt].dep=tree[last].dep; return; } int mid=(l+r)>>1; if (pos<=mid) merge(tree[last].lc,tree[rt].lc,l,mid,pos,to); else merge(tree[last].rc,tree[rt].rc,mid+1,r,pos,to); }
后面并查集的操作就和普通并查集一样就行!!!
void work_merge(int i,int x,int y)//在i-1的基础上合并x,y节点 { root[i]=root[i-1]; int fx=find(root[i],x); int fy=find(root[i],y); if (tree[fx].val!=tree[fy].val) { if (tree[fx].dep>tree[fy].dep) swap(fx,fy); merge(root[i-1],root[i],1,n,tree[fx].val,tree[fy].val); //深度小的fx连到深度大的fy去减小复杂度!!! if (tree[fx].dep==tree[fy].dep) update(root[i],1,n,tree[fy].val); //注意:是fx的深度小于fy的深度,所以要把fy的深度+1 } } bool work_find(int i,int x,int y) //找第i个版本x和y是不是在一个集合中 { root[i]=root[i-1]; int fx=find(root[i],x); int fy=find(root[i],y); return tree[fx].val==tree[fy].val; } void work_goback(int i,int id) //恢复到第id版本 { root[i]=root[id]; }
整个代码Code:

// luogu-judger-enable-o2 # include <bits/stdc++.h> using namespace std; const int N=2e5+10; struct Tree{ int val,lc,rc,dep; }tree[N*20]; int n,m,tot; int root[N*20]; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } void build(int &rt,int l,int r) { rt=++tot; if (l==r) { tree[rt].val=l; return;} int mid=(l+r)>>1; build(tree[rt].lc,l,mid); build(tree[rt].rc,mid+1,r); } void update(int rt,int l,int r,int pos) { if (l==r){ tree[rt].dep++; return ;} int mid=(l+r)>>1; if (pos<=mid) update(tree[rt].lc,l,mid,pos); else update(tree[rt].rc,mid+1,r,pos); } void merge(int last,int &rt,int l,int r,int pos,int to) { rt=++tot; tree[rt]=tree[last]; if (l==r) { tree[rt].val=to; tree[rt].dep=tree[last].dep; return; } int mid=(l+r)>>1; if (pos<=mid) merge(tree[last].lc,tree[rt].lc,l,mid,pos,to); else merge(tree[last].rc,tree[rt].rc,mid+1,r,pos,to); } int query(int rt,int l,int r,int pos) { if (l==r) return rt; int mid=(l+r)>>1; if (pos<=mid) return query(tree[rt].lc,l,mid,pos); else return query(tree[rt].rc,mid+1,r,pos); } int find(int rt,int pos) { int now=query(rt,1,n,pos); if (tree[now].val==pos) return now; return find(rt,tree[now].val); } void work_merge(int i,int x,int y) { root[i]=root[i-1]; int fx=find(root[i],x); int fy=find(root[i],y); if (tree[fx].val!=tree[fy].val) { if (tree[fx].dep>tree[fy].dep) swap(fx,fy); merge(root[i-1],root[i],1,n,tree[fx].val,tree[fy].val); if (tree[fx].dep==tree[fy].dep) update(root[i],1,n,tree[fy].val); } } bool work_find(int i,int x,int y) { root[i]=root[i-1]; int fx=find(root[i],x); int fy=find(root[i],y); return tree[fx].val==tree[fy].val; } void work_goback(int i,int id) { root[i]=root[id]; } int main() { n=read();m=read(); build(root[0],1,n); for (int i=1;i<=m;i++) { int op=read(); if (op==1) { int a=read(),b=read(); work_merge(i,a,b); } else if (op==2) { int k=read(); work_goback(i,k); } else if (op==3) { int a=read(),b=read(); putchar(work_find(i,a,b)+'0'); putchar('\n'); } } return 0; }
给个NOI2018的例题: P4768 [NOI2018]归程
还有可持久化Treap、可持久化Splay。
....
自闭了。
(未完待续)


