点分治学习笔记

/*
淀粉质真好吃！
*/

P4178 Tree

这个题概括起来就是：

求树上两点路径小于等于K的条数

这是点分治的传统题：维护树上的路径。

点分治的精髓：就是不断的把一棵树拆成几棵子树来处理，并且考虑路径的合并。

分治点的选择 :树的重心！

为什么呢？假设树的形态是一条链，那么每次取链头的理论时间复杂度是O(n²)

而每次取中间的时间复杂度是O(n log₂ n)此时中间就是树的重心，而一棵树可以看成无数的链拼接而成，

理应满足和链一样的性质，选重心的时候最优。可以达到近O(n log₂ n)的复杂度。

怎么求树的重心：每次找到子树中的一个点它的儿子恰好多于子树根的size[]/2

　　　　　　　　（就是它底下的儿子恰好比子树元素的一半多一点点）

得出这样的递归代码：

int Get_Root(int u,int fath,int S)
{
    int pos=0;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        if (size[v]>size[pos]) pos=v;
    }
    if (pos!=0&&size[pos]>=S/2) return Get_Root(pos,u,S);
    return u;
}

但是为了避免一些毒瘤题目卡树的重心，最好还是按照标准的来。

ps: 最大子树节点个数最少的点u就是重心，这样一个树形DP就行

void Get_Root(int u,int fath)
{
    f[u]=0,size[u]=1;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Root(v,u);
        f[u]=max(f[u],size[v]);
        size[u]+=size[v];
    }
    f[u]=max(f[u],SIZE-size[u]);
    if (f[u]<f[root]) root=u;
}

记得一开始f[0]=正无穷

然而点分治是怎么实现的呢？

先给出一个代码：

void solve(int u)
{
    ans=ans+Get_Ans(u,0);
    use[u]=true;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        ans=ans-Get_Ans(v,a[i].w);
        int rt=Get_Root(v,u,size[v]);
        solve(rt);
    }
}

ans指的是一个答案，use代表这个点之前有没有计算过（一旦这个点被记做重心，那么这个点就被用了）。

一开始加的这个ans指的是求解过u点的贡献。然后标记u的use是true

然后找一个子树，容斥原理除去非法答案

这里需要着重注意!!!

A为重心，当前分治到A点。

那么我们Get_Ans出来的答案应该是这么几条路径：

A-B

A-B-C

A-B-D

A-E

A-E-F

然而我们发现这样三条路径相互叠加是没有跨越A点的！

A-B

A-B-C

A-B-D

所以这三条路径相互叠加的我们需要减去，其实很简单就是找到子树的根B（分治点的直接儿子），减去子树的单独贡献就行。

这里需要把A-带上，增加在每一条路径前，所以就能减去非法答案了！

然后找到一个新的分治点分治。

对于这道题目： P4178 Tree

其实就是Get_Ans的问题：二分左端点不断逼近，右端点不断逼近就行了。

int Get_Ans(int u,int Len)
{
    d[cnt=0]=0;
    Get_Dist(u,0,Len);
    sort(d+1,d+1+cnt);
    int l=1,r=cnt,an=0;
    while (l<=r) {
        if (d[l]+d[r]<=k) an=an+r-l,l++;
        else r--;
    }
    return an;
}

整个代码的话长这样：（size在Get_Dist中一起做掉了）

# include <bits/stdc++.h>
# define fp(i,s,t) for (int i=s;i<=t;i++)
using namespace std;
const int N=40005;
int head[N],size[N],d[N],cnt,n,tot,ans,k;
bool use[N];
struct rec{int pre,to,w;}a[N<<1];
template<typename T>void read(T &x)
{
    x=0; int w=0; char c=0;
    while (c<'0'||c>'9') w|=c=='-',c=getchar();
    while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    x=w?-x:x;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args)
{
    read(t);read(args...);
}
void adde(int u,int v,int w)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    a[tot].w=w;
    head[u]=tot;
}
int Get_Root(int u,int fath,int S)
{
    int pos=0;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        if (size[v]>size[pos]) pos=v;
    }
    if (pos!=0&&size[pos]>=S/2) return Get_Root(pos,u,S);
    return u;
}
void Get_Dist(int u,int fath,int D)
{
    d[++cnt]=D; size[u]=1;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Dist(v,u,D+a[i].w);
        size[u]+=size[v];
    }
}
int Get_Ans(int u,int Len)
{
    d[cnt=0]=0;
    Get_Dist(u,0,Len);
    sort(d+1,d+1+cnt);
    int l=1,r=cnt,an=0;
    while (l<=r) {
        if (d[l]+d[r]<=k) an=an+r-l,l++;
        else r--;
    }
    return an;
}
void solve(int u)
{
    ans=ans+Get_Ans(u,0);
    use[u]=true;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        ans=ans-Get_Ans(v,a[i].w);
        int rt=Get_Root(v,u,size[v]);
        solve(rt);
    }
}
int main()
{
    read(n);
    int u,v,w,t;
    fp(i,2,n) read(u,v,w),adde(u,v,w),adde(v,u,w);
    read(k);
    solve(1);
    cout<<ans<<'\n';
    return 0;
}

View Code

但是为什么我学了点分治呢？？？

事情是这样的，这天翻译到一道试题，发现是一个关于xor的性质的题目。

马上就想到异或前缀和+Tire树。然后发现我看错题目了。

COCI 2018/2019 Problem3 Deblo

这道题概括起来就是：

求树上路径点权异或和之和

事实上这道题如果放在边权上直接就出来了！

你就可以跑一边dfs，记录xor前缀和，然后问题就转化为：求一个数组d(就是xor前缀和数组)，第l项和第r项(r>=l)相减(d[r]-d[l])，求和

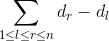
然后你弄个桶从左往右扫就完美O(n log₂ n)了。。

但是但是这个东西是点权，如果你那样做会抠掉LCA！！！

这样做的复杂度是O(n² log₂ n)？加点常数还不如O(n³)裸暴力？！

一定有高妙的办法。

淀粉质点分治是解决树上路径的利器

我们考虑到：树上路径的形成无外乎两种情况，在一棵以x为子树根的子树中，u到v的一条路径要么是跨过x，要么是不跨过x的。

进一步，如果u到v这条路径跨过x，那么 u和v要么同时在x的同一个子树里面，要么在同时在x不同的子树外！（看图）

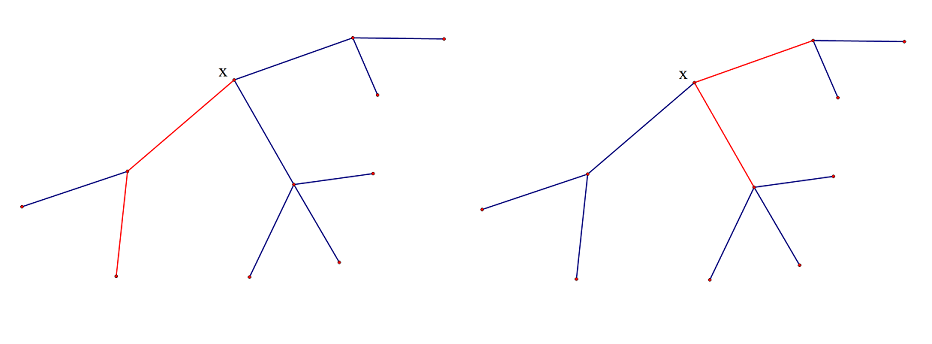
我们想到可以在确定一个子树根的情况下，分别遍历他的每一个子树，分别统计答案然后把答案“拼接”起来，形成最终要求的答案。

当然只分出一个根还不够，每一次深入我们都需要找到一个根，然后来遍历他的各个子树。

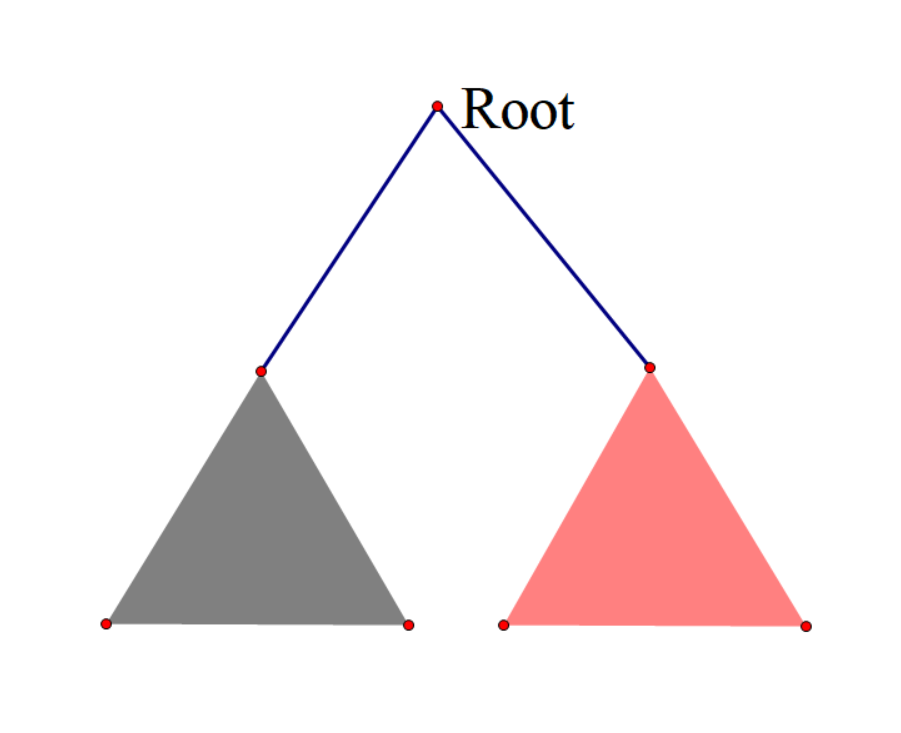
我们现在的模型就抽象成上面那样，一条合法的路径无外乎两种情况：

1. 灰色里面的一条过root的路径和红色里面一条过root的路径"拼接"起来

2.整条路径被灰色和红色子树包含

但是...要分类？

我们考虑分而治之：再细分会发生什么？

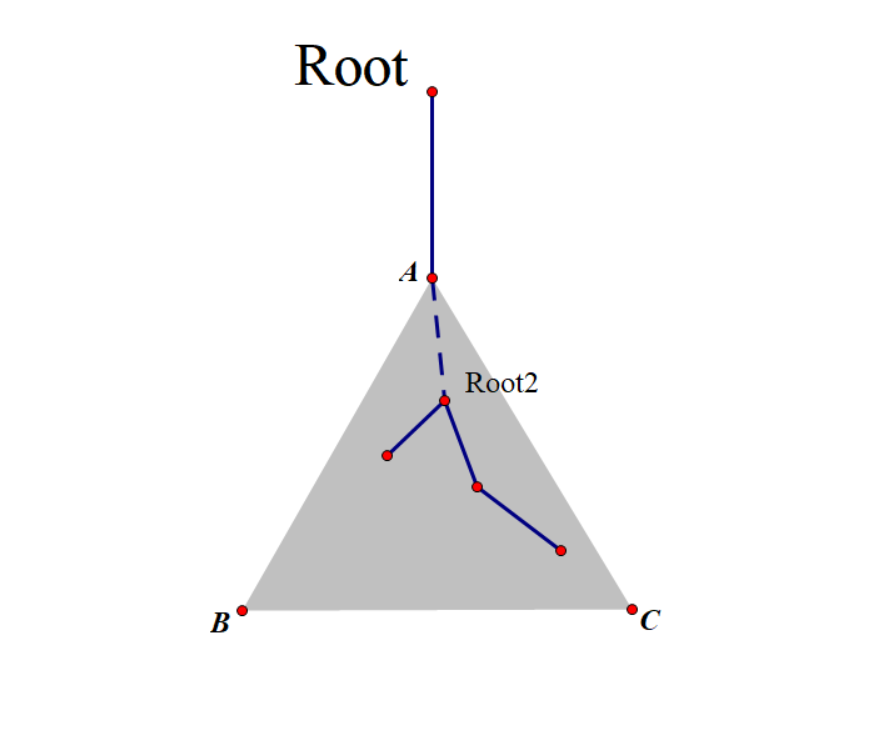
我们发现刚才的担心是多于，那是因为我只要逐步细分一定都可以作为第一种情况考虑，所以在分治的过程中我们只考虑第一种情况，不必要分类讨论。

那么怎么选root呢？这个事情就和树链剖分为什么剖长链一样，只是为了递归层数低一些。

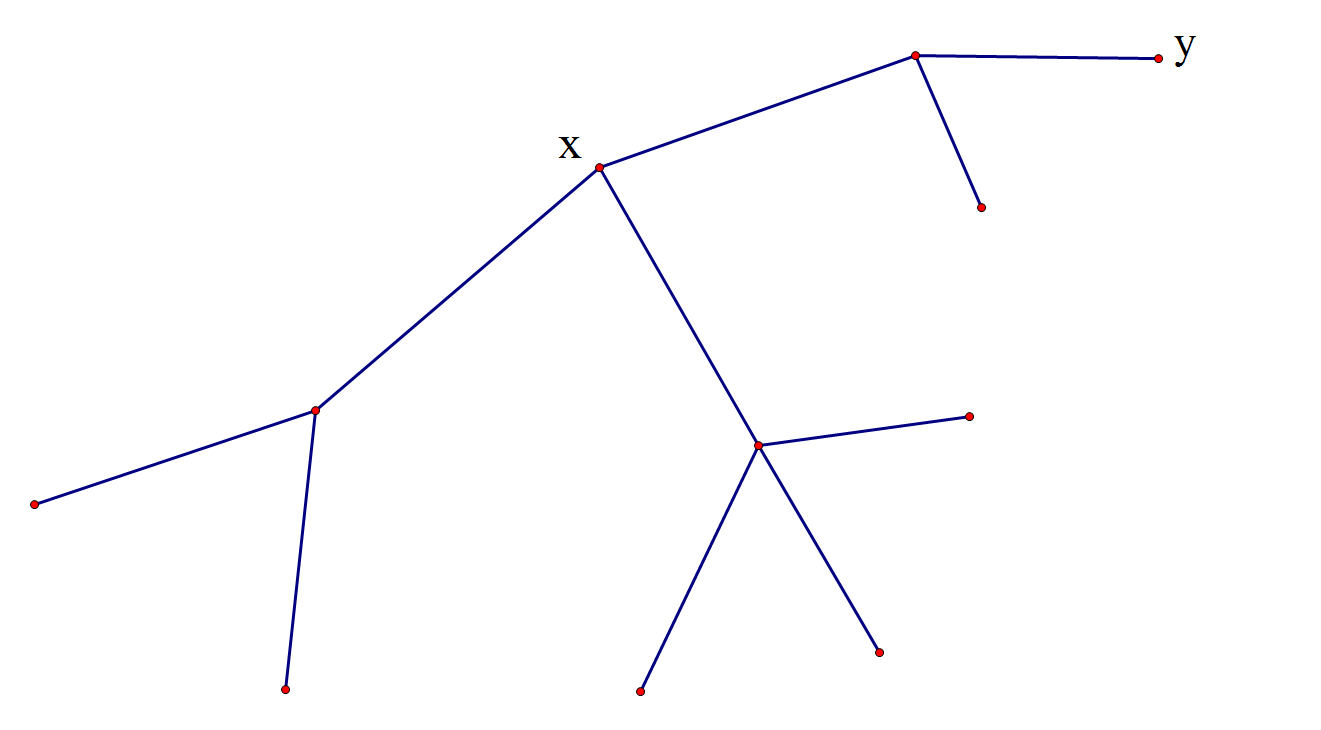
显然选X比选Y优，选X只要递归2层而选Y要递归4层！

一个结论：我们要选子树的重心！

我们对于重心的定义是这样的：这个点下面的子树元素个数占到整个子树元素个数的1/2还多一点点！

int Get_Root(int u,int fath,int S)//S是指以u为根的子树的size
{
    int pos=0;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||used[v]) continue;
        if (size[v]>size[pos]) pos=v;
    }
    if (pos!=0&&size[pos]>=S/2) return Get_Root(pos,u,S);
    return u;
}

根据重心的定义，我们可以写出这样一个得到以u为根子树的重心的函数。（复杂度O(n)）

找到子树的根了那么就可以算出以当前根root为子树根下面节点的异或前缀和。并把这些异或前缀和按照二进制位的方法存到一个桶cnt中。

注意到cnt[0][i]表示第i个二进制位是0的前面有多少个数，cnt1[1][i]表示第i个二进制位是1有多少个数。

由于异或运算不能像上面一样相减，我们考虑在处理完一棵子树以后再把这棵子树的信息加入到桶里面。

再来看Get_Dist函数，就相当于把以u为根的子树（含u）所涵盖节点异或前缀和加入到桶里面。

void Get_Dist(int u,int fath,int num)
{
    num^=val[u];
    fp(i,0,23)
     cnt[(num & (1<<i))>0][i]++;
    size[u]=1;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Dist(v,u,num);
        size[u]+=size[v];
    }
}

而Get_Ans函数，就相当于把以u为根的子树（含u）所涵盖节点异或前缀和和原有路径的异或前缀和进行异或，得到横跨节点u的一整条路径。

当然每次求一条路径必须不能包含这条路径上的节点（所以要先Get_Ans再Get_Dist！）

void Get_Ans(int u,int fath,int num)
{
    num^=val[u];
    fp(i,0,23)
     ans+=(LL)(1<<i)*cnt[(num & (1<<i))==0][i];
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Ans(v,u,num);
    }
}

至于根的问题由于横跨所有路径都会算上根，事先在solve中就已经把根加入桶了。

当然，我们没有考虑根到根这一条路径所以必须把它补上。

这就是solve函数了！！！

void solve(int u)
{
    use[u]=true;
    memset(cnt,0,sizeof(cnt));
    fp(i,0,23)
     cnt[(val[u] & (1<<i))>0][i]++;
    ans+=(LL)val[u];
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        Get_Ans(v,0,0);
        Get_Dist(v,0,val[u]);
    }
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        int rt=Get_Root(v,u,size[v]);
        solve(rt);
    }
}

这里有个复杂度的问题：我们在点分治过程中每次选取子树的重心为子树的树根进行处理，这样总的递归深度不会超过

# include <bits/stdc++.h>
# define fp(i,s,t) for (int i=s;i<=t;i++)
# define LL long long
using namespace std;
const int N=100005;
int head[N],size[N],d[N],n,tot,k;
bool use[N];
struct rec{int pre,to;}a[N<<1];
int cnt[2][25],val[N];
LL ans;
template<typename T>void read(T &x)
{
    x=0; int w=0; char c=0;
    while (c<'0'||c>'9') w|=c=='-',c=getchar();
    while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    x=w?-x:x;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args)
{
    read(t);read(args...);
}
void adde(int u,int v)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    head[u]=tot;
}
int Get_Root(int u,int fath,int S)
{
    int pos=0;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        if (size[v]>size[pos]) pos=v;
    }
    if (pos!=0&&size[pos]>=S/2) return Get_Root(pos,u,S);
    return u;
}
void Get_Dist(int u,int fath,int num)
{
    num^=val[u];
    fp(i,0,23)
     cnt[(num & (1<<i))>0][i]++;
    size[u]=1;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Dist(v,u,num);
        size[u]+=size[v];
    }
}
void Get_Ans(int u,int fath,int num)
{
    num^=val[u];
    fp(i,0,23)
     ans+=(LL)(1<<i)*cnt[(num & (1<<i))==0][i];
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Ans(v,u,num);
    }
}
void solve(int u)
{
    use[u]=true;
    memset(cnt,0,sizeof(cnt));
    fp(i,0,23)
     cnt[(val[u] & (1<<i))>0][i]++;
    ans+=(LL)val[u];
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        Get_Ans(v,0,0);
        Get_Dist(v,0,val[u]);
    }
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        int rt=Get_Root(v,u,size[v]);
        solve(rt);
    }
}
int main()
{
    read(n);
    int u,v;
    fp(i,1,n) read(val[i]);
    fp(i,2,n) read(u,v),adde(u,v),adde(v,u);
    solve(1);
    cout<<ans<<'\n';
    return 0;
}

View Code

我推荐几个练习（雾）：

【luogu P2634】 [国家集训队]聪聪可可

# include <cstdio>
# define LL long long
using namespace std;
const int N=5e4+10;
struct rec{ int pre,to,w; }a[N<<1];
int n,tot,ans,SIZE,root;
int head[N],d[N],size[N],f[N];
int r[3];
bool use[N];
int max(int x,int y){return (x>y)?x:y;}
int min(int x,int y){return (x>y)?y:x;}
inline int read()
{
    int X=0,w=0; char c=0;
    while(c<'0'||c>'9') {w|=c=='-';c=getchar();}
    while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar();
    return w?-X:X;
}
void adde(int u,int v,int w)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    a[tot].w=w;
    head[u]=tot;
}
void Get_Root(int u,int fath)
{
    f[u]=0,size[u]=1;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Root(v,u);
        f[u]=max(f[u],size[v]);
        size[u]+=size[v];
    }
    f[u]=max(f[u],SIZE-size[u]);
    if (f[u]<f[root]) root=u;
}
int cnt;
void Get_Dist(int u,int fath,int L)
{
    r[L%3]++;
    d[++cnt]=L; size[u]=1;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Dist(v,u,L+a[i].w);
        size[u]+=size[v];
    }
}
int Get_Ans(int u,int fath,int L)
{
    cnt=0; int ret=0;
    r[0]=r[1]=r[2]=0;
    Get_Dist(u,fath,L);
    for (int i=1;i<=cnt;i++)
     if (d[i]%3==0) ret+=r[0]-1;
     else if (d[i]%3==1) ret+=r[2];
     else if (d[i]%3==2) ret+=r[1];
    return ret;
}
void solve(int u)
{
    use[u]=true;
    ans+=(LL)Get_Ans(u,0,0);
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to; if (use[v]) continue;
        ans-=(LL)Get_Ans(v,u,a[i].w);
        SIZE=size[v],root=0;
        Get_Root(v,u);
        solve(root);
    }
}
LL gcd(LL a,LL b){return (b==0ll)?a:gcd(b,a%b);}
int main()
{
    f[0]=1e9; n=read();
    int u,v,w;
    for (int i=1;i<n;i++) {
        u=read();v=read();w=read();
        adde(u,v,w); adde(v,u,w);
    }
    SIZE=n; root=0;
    Get_Root(1,0);
    solve(root); ans+=(LL)n;
    LL g=gcd(ans,n*n);
    LL a=ans/g,b=(LL)n*n/g;
    printf("%lld/%lld",a,b);
    return 0;
}

View Code

【luogu模板】点分治1 询问树上距离为k的点对是否存在

# pragma G++ optimize(3)
# include <bits/stdc++.h>
using namespace std;
const int N=1e4+10;
struct rec{int pre,to,w;}a[N<<1];
int d[N],q[N],head[N],size[N],tot,n,m;
bool use[N];
int  bo[10000000];
void read(int& x)
{
    x=0;char c=0; bool w=false;
    while (c<'0'||c>'9') w|=c=='-',c=getchar();
    while ('0'<=c&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    if (w) x=-x;
}
void adde(int u,int v,int w)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    a[tot].w=w;
    head[u]=tot;
}
int Get_Root(int u,int fath,int S)
{
    int pos=0;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        if (size[v]>size[pos]) pos=v;
    }
    if (pos!=0&&size[pos]>=(S>>1)) return Get_Root(pos,u,S);
    return u;
}
int cnt;
void Get_Dist(int u,int fath,int L)
{
    d[++cnt]=L; size[u]=1;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Dist(v,u,L+a[i].w);
        size[u]+=size[v];
    }
}
void Get_Ans(int u,int L,int opx)
{
    cnt=0;
    Get_Dist(u,0,L);
    for (int i=1;i<=cnt;i++)
     for (int j=1;j<=cnt;j++)
      if (i!=j) bo[d[i]+d[j]]+=opx;
}
void solve(int u)
{
    Get_Ans(u,0,1);
    use[u]=true;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (use[v]) continue;
        Get_Ans(v,a[i].w,-1);
        int rt=Get_Root(v,0,size[v]);
        solve(rt);
    }
}
int main()
{
    read(n);read(m);
    int u,v,w;
    for (int i=1;i<n;i++)
     read(u),read(v),read(w),
     adde(u,v,w),adde(v,u,w);
    solve(1);
    int t;
    for (int i=1;i<=m;i++) {
        read(t);
        puts(bo[t]?"AYE":"NAY");
    }
    return 0;
}

View Code

【luogu P4178】 Tree 求小于k的点对个数

# include <bits/stdc++.h>
# define fp(i,s,t) for (int i=s;i<=t;i++)
using namespace std;
const int N=40005;
int head[N],size[N],d[N],cnt,n,tot,ans,k;
bool use[N];
struct rec{int pre,to,w;}a[N<<1];
template<typename T>void read(T &x)
{
    x=0; int w=0; char c=0;
    while (c<'0'||c>'9') w|=c=='-',c=getchar();
    while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    x=w?-x:x;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args)
{
    read(t);read(args...);
}
void adde(int u,int v,int w)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    a[tot].w=w;
    head[u]=tot;
}
int Get_Root(int u,int fath,int S)
{
    int pos=0;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        if (size[v]>size[pos]) pos=v;
    }
    if (pos!=0&&size[pos]>=S/2) return Get_Root(pos,u,S);
    return u;
}
void Get_Dist(int u,int fath,int D)
{
    d[++cnt]=D; size[u]=1;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Dist(v,u,D+a[i].w);
        size[u]+=size[v];
    }
}
int Get_Ans(int u,int Len)
{
    d[cnt=0]=0;
    Get_Dist(u,0,Len);
    sort(d+1,d+1+cnt);
    int l=1,r=cnt,an=0;
    while (l<=r) {
        if (d[l]+d[r]<=k) an=an+r-l,l++;
        else r--;
    }
    return an;
}
void solve(int u)
{
    ans=ans+Get_Ans(u,0);
    use[u]=true;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        ans=ans-Get_Ans(v,a[i].w);
        int rt=Get_Root(v,u,size[v]);
        solve(rt);
    }
}
int main()
{
    read(n);
    int u,v,w,t;
    fp(i,2,n) read(u,v,w),adde(u,v,w),adde(v,u,w);
    read(k);
    solve(1);
    cout<<ans<<'\n';
    return 0;
}

View Code

【CF161D】：求距离为k的点对个数

# pragma G++ optimize(3)
# include <bits/stdc++.h>
# define LL long long
using namespace std;
const int N=5e4+10;
struct rec{ int pre,to; }a[N<<1];
int n,k,tot;
LL ans;
int d[N],size[N],head[N];
bool use[N];
void read(int& x)
{
    x=0;char c=0; bool w=false;
    while (c<'0'||c>'9') w|=c=='-',c=getchar();
    while ('0'<=c&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    if (w) x=-x;
}
void adde(int u,int v)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    head[u]=tot;
}
int Get_Root(int u,int fath,int S)
{
    int pos=0;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        if (size[v]>size[pos]) pos=v;
    }
    if (pos!=0&&size[pos]>=(S>>1)) return Get_Root(pos,u,S);
    return u;
}
int cnt;
void Get_Dist(int u,int fath,int L)
{
    d[++cnt]=L; size[u]=1;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Dist(v,u,L+1);
        size[u]+=size[v];
    }
}
void Get_Ans(int u,int L,int opx)
{
    cnt=0; Get_Dist(u,0,L);
    sort(d+1,d+1+cnt);
    for (int i=1;i<=cnt;i++) {
     int *p1=lower_bound(d+1,d+1+cnt,k-d[i]);
     int t1=p1-d;
     int *p2=upper_bound(d+1,d+1+cnt,k-d[i]);
     int t2=p2-d-1;
     if (t2<t1) continue;
     if (t1==0||t2==0) continue;
     if ((d[t1]!=k-d[i])||(d[t2]!=k-d[i])) continue;
     ans+=(LL)(opx)*(t2-t1+1);
     if (i>=t1&&i<=t2) ans-=opx;
    }
}
void solve(int u)
{
    use[u]=true;
    Get_Ans(u,0,1);
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        Get_Ans(v,1,-1);
        int rt=Get_Root(v,0,size[v]);
        solve(rt);
    }
}
signed main()
{
     read(n);read(k);
    int u,v;
    for (int i=1;i<n;i++)
        read(u),read(v),
        adde(u,v),adde(v,u);
    solve(1);
    cout<<(ans>>1)<<'\n';
    return 0;
}

View Code

[IOI2011]Race ：权值和为k，求最小边数

# include <cstdio>
# define inf (0x3f3f3f3f)
using namespace std;
const int N=2e5+10;
const int K=1e6+10;
struct rec { int pre,to,w; }a[N<<1];
int n,k,tot,ans=inf,root,SIZE;
int head[N],size[N],tmp[K],f[N];
bool use[N];
inline int min(int x,int y){ return x>y?y:x;}
inline int max(int x,int y){ return x>y?x:y;}
inline int read(int &X)
{
    X=0; bool w=0; char c=0;
    while(c<'0'||c>'9') {w|=c=='-';c=getchar();}
    while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar();
    return w?-X:X;
}
void adde(int u,int v,int w)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    a[tot].w=w;
    head[u]=tot;
}
void Get_Root(int u,int fath)
{
    f[u]=0,size[u]=1;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Root(v,u);
        f[u]=max(f[u],size[v]);
        size[u]+=size[v];
    }
    f[u]=max(f[u],SIZE-size[u]);
    if (f[u]<f[root]) root=u;
}
void Get_Dist(int u,int fath,int num,int L)
{
    if (L>k) return;
    tmp[L]=min(tmp[L],num);
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Dist(v,u,num+1,L+a[i].w);
    }
}
void Get_Ans(int u,int fath,int num,int L)
{
    if (L>k) return;
    ans=min(ans,tmp[k-L]+num);
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        Get_Ans(v,u,num+1,L+a[i].w);
    }
}
void clear(int u,int fath,int L)
{
    if (L>=k) return;
    tmp[L]=inf;
    for (int i=head[u];i;i=a[i].pre){
        int v=a[i].to;
        if (v==fath||use[v]) continue;
        clear(v,u,L+a[i].w);
    }
}
void solve(int u)
{
    use[u]=true; tmp[0]=0;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        Get_Ans(v,u,1,a[i].w);
        Get_Dist(v,u,1,a[i].w);
    }
    clear(u,0,0);
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to;
        if (use[v]) continue;
        SIZE=size[v],root=0;
        Get_Root(v,u);
        solve(root);
    }
}
int main()
{
    read(n);read(k); f[0]=inf;
    for (int i=1;i<n;i++) {
        int u,v,w;
        read(u);read(v);read(w);
        adde(u+1,v+1,w); adde(v+1,u+1,w);
    }
    for (int i=0;i<=k;i++) tmp[i]=inf;
    SIZE=n,root=0; Get_Root(1,0);
    solve(root);
    if (ans==inf) puts("-1");
    else printf("%d\n",ans);
    return 0;
}

View Code

posted @ 2019-02-01 22:27 ljc20020730 阅读(267) 评论(0) 编辑收藏举报

刷新页面返回顶部

ljc20020730

hi！我回来啦！这次带来一个好消息！我回来啦作为一个ACMer. 我的新博客是cnblogs.com/maystern 做了美化哦！快来看看吧。

点分治学习笔记

P4178 Tree

COCI 2018/2019 Problem3 Deblo

【luogu P2634】 [国家集训队]聪聪可可

【luogu模板】点分治1 询问树上距离为k的点对是否存在

【luogu P4178】 Tree 求小于k的点对个数

[IOI2011]Race ：权值和为k，求最小边数

公告