HGOI20190126 模拟赛

/*
最后一题比较难！
*/

 

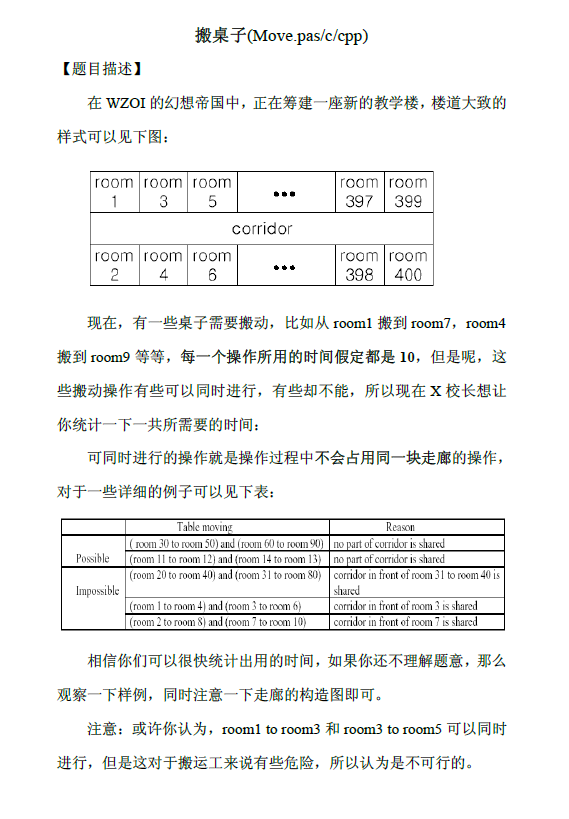
solution：观察这个奇怪的图，不能共用走廊，就是1.2打包，3,4打包，每个包之间连线的线段覆盖问题。

考虑吧每个数映射成一个约为一半的数，且相邻(前奇后偶映射值一样)，如1.2映射为1且3.4映射为2，(2x-1.2x)映射成x

然后线段覆盖，用差分维护即可。

# include <bits/stdc++.h>
using namespace std;
const int MAXN=1405;
int s[MAXN],c[MAXN];
int n;
inline int read()
{
    int X=0,w=0;char c=0;
    while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar();
    while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar();
    return w?-X:X;
}
void add(int l,int r)
{
    c[l]++; c[r+1]--;
}
int main()
{
    n=read();
    for (int i=1;i<=n;i++) {
        int l=(read()+1)/2,r=(read()+1)/2;
        if (l>r) swap(l,r);
        add(l,r);
    }
    for (int i=1;i<=400;i++) s[i]=s[i-1]+c[i];
    int ans=0;
    for (int i=1;i<=400;i++) ans=max(ans,s[i]);
    printf("%d\n",ans*10); 
    return 0;
}

solution：可以字符串哈希、可以字典树、可以直接hash映射！

# include <bits/stdc++.h>
using namespace std;
const int N=70005;
char s[N],A[N];
int ans;
struct tt{
    int ch[N][128],size;
    int val[N];
    tt(){
        size=1;
        memset(ch[0],0,sizeof(ch[0]));
        memset(val,0,sizeof(val));  
    }
    int idx(char a) { return a;}
    void insert()
    {
        int u=0,len=strlen(s);
        for (int i=0;i<len;i++) {
            int c=idx(s[i]);
            if (!ch[u][c]) {
                memset(ch[size],0,sizeof(ch[size]));
                ch[u][c]=++size;
            }
            u=ch[u][c];
        }
        val[u]++;
        if (val[u]>ans) {
            ans=val[u];
            memcpy(A,s,sizeof(s));
        }
    }
}Tree;
int main()
{
    int  T; scanf("%d",&T);
    while (T--) {
        scanf("%s",s);
        Tree.insert();
    }
    printf("%s %d\n",A,ans);
    return 0;
}

solution：这道题就是最小化

可以证明，d是a_i中位数时最小！

# include <bits/stdc++.h>
# define int long long
using namespace std;
const int N=2e6+10;
int a[N],n,o,ans;
inline int read()
{
    int X=0,w=0;char c=0;
    while (!(c>='0'&&c<='9')) w|=c=='-',c=getchar();
    while (c>='0'&&c<='9') X=(X<<1)+(X<<3)+(c^48),c=getchar();
    return w?-X:X;
}
signed main()
{
    n=read();
    for (int i=1;i<=n;i++) read(),a[i]=read();
    sort(a+1,a+1+n);
    if (n&1) o=a[n/2+1]; else o=(a[n/2]+a[n/2+1])/2;
    for (int i=1;i<=n;i++) ans=ans+abs(o-a[i]);
    printf("%lld\n",ans); 
    return 0;
}