基础数论
/*
今天的基础数论我觉得我还是重新温习一下比较好！
*/
时光真的是个迷，第二次重新听当年初二XX学堂讲数论突然觉得好亲切！
我还是写写吧，应该很清楚！希望对大家有点用！
知识点1：快速幂（卡粟米）
求ap其实可以用分治的思想来求
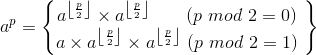
就是不断的分治，直到p=0，返回1.
递归写法：
const int mo=100000007; int pow(int x,int n) { if (n==0) return 1; if (n==1) return x; int t=pow(x,n/2)%mo; t=t*t%mo; if (n%2) t=t*x%mo; return t; }
非递归写法：
int pow(int x,int n,int p) { int ans=1; while (n) { if (n&1) ans=ans*x%p; x=x*x%p; n>>=1; } return ans%p; }
知识点2：质数
定理1：唯一分解定理（任何大于2正整数都可以表示成为多个质数相乘的形式，并且分解唯一）
定理2：素数判断定理（当且仅当不存在任意1<k<=（下取整） √x，使得x mod k = 0，那么x为质数）
定理3：整数1，既不是质数又不是合数！
质数的判定：（试除法O（√x）、非完美算法米勒罗宾随机算法）
埃拉托斯特尼筛法求质数O(n log log n)
- 若x是质数那么从x2开始，把x的倍数筛去。
void EratosthenesSha(int n) { memset(prime,true,sizeof(prime)); vector<int>a;a.clear(); for (int i=2;i<=n;i++) { if (prime[i]==false) continue; a.push_back(i); for (int j=i+i;j<=n;j+=i) prime[j]=false; } }
欧拉线性筛法求质数O(n)
- 每个合数都只筛一次（用最小质因子筛去），给当前的数i乘上一个质因子，有更小的质因子或者超出范围break
- 为什么？由于i若是prime[j]的倍数，i*prime[j+1]（等）一定被筛过：由于i=k*prime[j]，i*prime[j+1]=k*prime[j]*prime[j+1]这个数i*prime[j]最小质因子一定不是prime[j+1]不用删去，这样就保证每个数删去一次！
void EouLaSha(int lim) { int cnt=0; pr[0]=pr[1]=true; for (int i=2;i<=lim;i++) { if (!pr[i]) prime[cnt++]=i; for (int j=0;j<cnt&&i*prime[j]<=lim;j++) { pr[i*prime[j]]=true; if (i%prime[j]==0) break; } } }
知识点3：gcd和exgcd（扩展欧几里得）
- gcd（欧几里得算法）
求出gcd(a,b)就是求出a和b的最大公因数。
定理： gcd(a,b)=gcd(b,a%b)
证明：∀r，满足r|a，r|b; 而
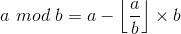
r|a mod b 且 r|b
由定义可知，r|a,r|b且r任意，可以为a，b的最大公因数。
证毕。
int gcd(int a,int b) { if (b==0) return a; return simple_gcd(b,a%b); // 代码更短： return (!b)?a:simple_gcd(b,a%b); }
- exgcd（扩展欧几里得算法）
对于下列不定方程，必有一对整数解，我们可以通过exgcd求出|x|+|y|最小的一对！
易得4个方程：
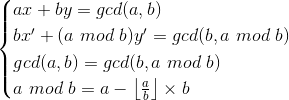
联立解之得（用x'表示x，y’表示y，a和b是常数）：
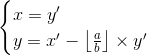
特别的，当b=0的时候，方程组变成了ax=gcd(a,0)=a，得a=1，人为定义y=0
int ex_gcd(int a,int b,int &x,int &y) { if (b==0) { x=1;y=0; return a; } int r=ex_gcd(b,a%b,x,y); int t=x;x=y;y=t-a/b*y; return r; }
知识点4：同余方程和同余方程
同余的定义：若a mod p = b mod p ，那么称a与b关于p同余，记作a≡b (mod p)
同余的定理：
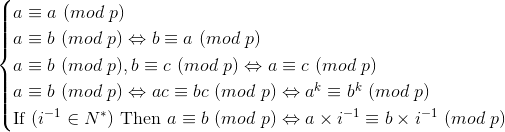
乘法逆元的定义:若ax≡1（mod p），那么称x为a在模p意义下的逆(元),记做 a-1
求逆元的方法
快速幂求逆元：
费马小定理：若p为素数，a为正整数，且a和p互质，有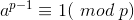 
推出：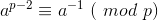
/* 基于费马小定理pow(a,p-2)%p 就是a在mod p意义下的逆元 */ int pow(int x,int n,int m) { if (n==0) return 1; if (n==1) return x; int t=pow(x,n/2,m)%m; t=t*t%m; if (n%2) t=t*x%m; return t; } int inv(int x,int m) { return pow(x,m-2,m)%m; }
扩展欧几里得求逆元
c=1 时 等价于：
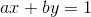
求出x的正根即可
/* 求ax=1(mod p) 就是求ax%p=1,所以ax ax=kp+1,就是ax-kp=1， 当p为质数的时候gcd(a,-p)=1，求此时x的值就是逆元 注意模到正数就行 */ int ex_gcd(int a,int b,int &x,int &y) { if (b==0) { x=1;y=0; return a; } int r=ex_gcd(b,a%b,x,y); int t=x;x=y;y=t-a/b*y; return r; } int inv(int a,int m) { int x,y; int g=ex_gcd(a,m,x,y); return (x+m)%m; }
筛选法求逆元
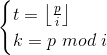
有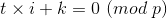 
两边乘上 i-1k-1
得：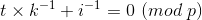
那么，
即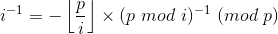 
void getinv(int x,int p) { memset(inv,0,sizeof(inv)); inv[1]=1; for (int i=2;i<=x;i++) inv[i]=(long long)(p-p/i)%p*inv[p%i]%p; }
知识点5：欧拉函数
定义：φ(x)表示[1,x)内正整数和x互质（最大公约数为1）的数的个数。
求法：
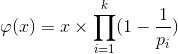
性质：
- 积性函数：若gcd(n,m)=1,φ(nm)=φ(n)φ(m)
- φ(x) 为偶数 （x>2）
- 与n互质的数的总和为：φ(n) * n / 2 (n>1)
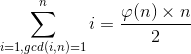
- n的因数（包括1和它自己）的欧拉函数之和等于n
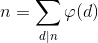
埃拉托斯特尼筛求欧拉函数
void getphi(int x) { memset(phi,0,sizeof(phi)); phi[1]=1; for (int i=2;i<=x;i++) if (phi[i]==0) { for (int j=i;j<=x;j+=i){ if (phi[j]==0) phi[j]=j; phi[j]=phi[j]/i*(i-1); } } }
欧拉筛求欧拉函数
i表示当前做到的这个数，prime[j]表示当前做到的质数，那要被筛掉的合数就是i*prime[j]
若prime[j]在这个合数里只出现一次（i mod prime[j] ≠ 0），也就是 i 和 prime[j] 互质时，
则根据欧拉函数的积性函数的性质，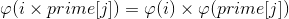
若prime[j]在这个合数里出现了不止一次（i mod prime[j]=0），也就是这个合数的所有质因子都在i里出现过，
void getphi(int n) { phi[1]=1;//1要特判 for (int i=2;i<=n;i++) { if (flag[i]==0)//这代表i是质数 { prime[++num]=i; phi[i]=i-1; } for (int j=1;j<=num&&prime[j]*i<=n;j++)//经典的欧拉筛写法 { flag[i*prime[j]]=1;//先把这个合数标记掉 if (i%prime[j]==0) { phi[i*prime[j]]=phi[i]*prime[j];//若prime[j]是i的质因子，则根据计算公式，i已经包括i*prime[j]的所有质因子 break;//经典欧拉筛的核心语句，这样能保证每个数只会被自己最小的因子筛掉一次 } else phi[i*prime[j]]=phi[i]*phi[prime[j]];//利用了欧拉函数是个积性函数的性质 } } }
知识点5：BSGS算法（Baby Step Gaint Step）
这个算法的别称有很多：“拔山盖世“、"北上广深"、”百度搜索谷歌搜索“
解决的是这么一个问题：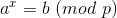 
当p为质数，a,b是整数，规定 
的时候
最小化x的值并输出。
令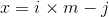 
, 其中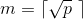 
原式变成 ：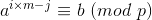 
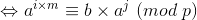
现在做一件事，枚举j∈[0,m] ， 把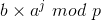 
存入Hash表
然后枚举i∈[1,m]，从Hash表中找出第一个有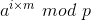 
的映射 j，
此时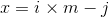 
就是所求
一个模板题: P3846 [TJOI2007]可爱的质数
code :
# include <bits/stdc++.h> # define int long long using namespace std; int p,a,b; map<int,int>Hash; int pow(int x,int n,int p) { int ans=1; while (n) { if (n&1) ans=ans*x%p; x=x*x%p; n>>=1; } return ans; } signed main() { scanf("%lld%lld%lld",&p,&a,&b); int m=ceil(sqrt(p)); Hash.clear(); Hash[b]=0; int s=b; for (int j=1;j<=m;j++) { s=s*a%p; Hash[s]=j; } s=pow(a,m,p); int t=s; for (int i=1;i<=m;i++) { if (Hash.count(s)>0) { printf("%lld\n",((i*m%p-Hash[s]%p)%+p)%p); exit(0); } s=s*t%p; } puts("no solution"); return 0; }
