杭高OI20190125 (genies出题)
/*
当一个人先从自己的内心开始奋斗,他就开始迈向了成功
——genies (朝阳的二愣子)
*/HGOI寒假赛第一场,欢迎来自各种学校的各式各样的巨老233333
感觉自己好渺小。还是NOIP (pj)的模拟题吧,也有AK的,不过我是下划线开头,所以我来讲咯。
踩了std,(还有xyc大佬踩了标程!他比我快!),感觉还是挺水的。
自己还是要提高(下午讲了数论,相信高一党没怎么听懂23333)
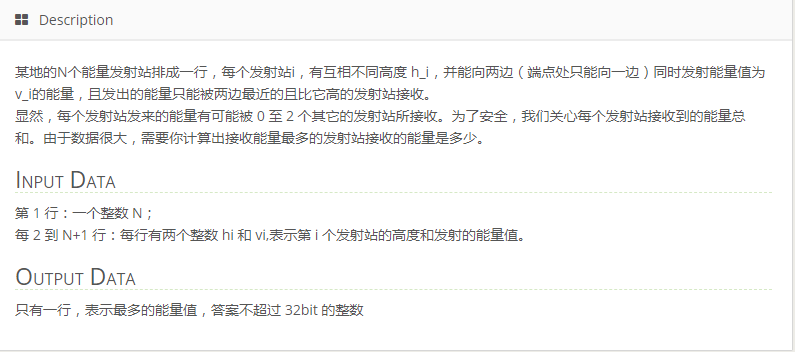
T1 发射站(fsz)
solution:就是单调栈的题目,由于是数据听说比较强然后打了手写栈!结果就不说了吧(n方tm都能过!)
思路挺简单就是第一遍找第一个右侧比他高的,能量给高的(在弹栈的时候),显然需要维护一个h单调不增的栈,每次插入一个元素的时候弹出元素,
并把弹出元素的能量v累加到即将插入的元素i上,然后正反搞2遍,扫一遍ans就出来了!(我是不会告诉你我这道题打了1h10min的!)
code:

# include<bits/stdc++.h> # define int long long using namespace std; const int N=1e6+10; struct rec{ int h,v; }a[N]; int n,ans[N]; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } struct sta{ int Top; rec s[N]; sta(){Top=0;} bool empty() {return (Top==0);} void push(rec x){s[++Top]=x;} void pop(){ Top--;} void clear(){ Top=0;}; rec top(){return s[Top];} }s; signed main() { n=read(); for (int i=1;i<=n;i++) a[i].h=read(),a[i].v=read(); for (int i=1;i<=n;i++) { if (s.empty()) { s.push(a[i]); continue; } while (!s.empty()&&s.top().h<a[i].h) { ans[i]+=s.top().v; s.pop(); } s.push(a[i]); } s.clear(); for (int i=n;i>=1;i--) { if (s.empty()) { s.push(a[i]); continue; } while (!s.empty()&&s.top().h<a[i].h) { ans[i]+=s.top().v; s.pop(); } s.push(a[i]); } int Ans=0; for (int i=1;i<=n;i++) Ans=max(Ans,ans[i]); printf("%lld\n",Ans); return 0; }
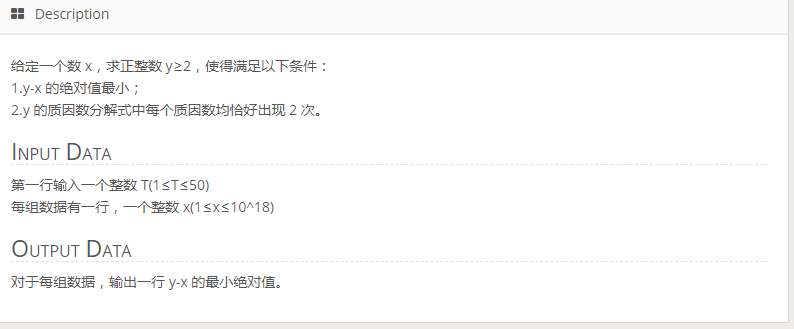
T2 绝对值(abs)
solution:思路也是显然的;需要的时间复杂度是O(T * 4√x )
考虑一个数y合法(每个质因数出现2次)那么有 √y 每个质因数出现1次!
知道这个结论,对于每一个x,我们在线在(下取整)√x左右偏移step个单位,构造出x‘=(√x+step)2然后在可行的情况下
最小化| x'2 - x |就行,但是需要考虑一个边界问题,什么时候单调,由于√x是下取整,那么√x和√x+1是一对,
如此类推√x-1和√x+2是一对,则有√x-step和√x+step+1是一对,step∈[0,+∞),这样就有单调性!
还有那个筛素数实际上只要筛到4√x 就行了,就是1e5!

# include <bits/stdc++.h> # define int long long using namespace std; const int N=1e5+10; bool pr[N]; int last[N]; vector<int>a; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } void getprime(int Lim) { memset(pr,true,sizeof(pr)); pr[0]=pr[1]=false; for (int i=2;i<=Lim;i++) { if (!pr[i]) continue; a.push_back(i); for (int j=i+i;j<=Lim;j+=i) pr[j]=false; } } bool check(int x) { if (x<0) return false; int p=0,cnt; for (;;){ int nowprime=a[p]; if (nowprime>x||p==a.size()-1) break; cnt=0; while (x%nowprime==0) cnt++,x/=nowprime; if (cnt>1) return false; p++; } return true; } # define SQR(x) ((x)*(x)) int work(int x) { int base=sqrt(x); int step=0; while (true) { bool g1=check(base+step+1); bool g2=check(base-step); if (g1&&g2) { if (abs(x-SQR(base+step+1))<abs(x-SQR(base-step))) return base+step+1; else return base-step; } else if (g1) return base+step+1; else if (g2) return base-step; step++; } } void write(int x) { if (x>9) write(x/10); putchar('0'+x%10); } void writeln(int x) { write(x); putchar('\n'); } signed main() { getprime(1e5); int T=read(); while (T--) { int x=read(); writeln(abs(x-SQR(work(x)))); } return 0; }
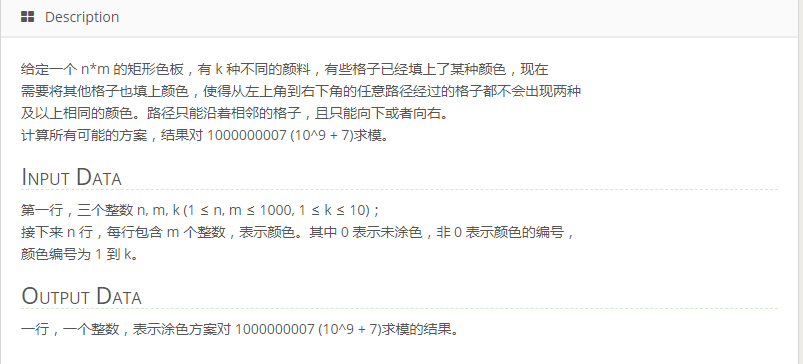
T3 独特的路径(path)
solution:一开始看成状压orz,怎么存不下状态鸭(滑稽),后来发现看错题了。搜索题!
首先需要知道这么一个东西,如果走到这个点(x,y)用掉了c种颜色,然而要走到(n,m)才算成功,
那么之后(从(x,y)走到(n,m))至少还需要用掉 n-(x-1)+m-(y-1)-1=n-x+m-y+1 种颜色
特殊的,从(1,1)走到(n,m)需要经过n+m-1个格子.
发现这一条性质30%的分数就有了,开局特判k和n,m的关系。若(n+m-1>k)输出0
然后搜索剪枝,顺序需要保证左上角矩阵出现过的元素不能在此格子填写,所以左上角必须搜完,采用从左往右,从上到下的形式搜!
剪枝:
- 可行性:到(x,y)看剩下的颜色够不够即前面用掉c种,那么若(n-x+m-y+1)>k-c那么直接不可以。
- 对偶性:.在填某一个格子时,如果某些颜色在之前没有使用过,那么他们的情况数都是相同的。(如果之前用过就不一定了!)
不要忘记膜
code:

# include <bits/stdc++.h> # define int long long using namespace std; const int N=1e3+10; const int mo=1e9+7; const int BIT=11; int mp[N][N],f[N][N],num[BIT]; int n,m,k; inline int read() { int X=0,w=0; char c=0; while(c<'0'||c>'9') {w|=c=='-';c=getchar();} while(c>='0'&&c<='9') X=(X<<3)+(X<<1)+(c^48),c=getchar(); return w?-X:X; } # define lowbit(x) ((x)&(-x)) # define bit_place(x) (trunc(log(x+0.5)/log(2))) int bit_count(int x) { int cc=0; for (int i=x;i;i-=lowbit(i)) cc++; return cc; } int dfs(int x,int y) { if (y>m) x=x+1,y=1; if (x>n) return 1; f[x][y]=f[x-1][y]|f[x][y-1]; if (n-x+m-y+1>k-bit_count(f[x][y])) return 0; int qwq=-1,sum=0; for (int base=(~f[x][y])&((1<<k)-1);base;base-=lowbit(base)) { int d=lowbit(base); int col=bit_place(d)+1; if (mp[x][y]==0||mp[x][y]==col) { int record=f[x][y]; f[x][y]=f[x][y]|d; num[col]++; if (num[col]==1) { if (qwq==-1) qwq=dfs(x,y+1); sum=(sum+qwq)%mo; } else sum=(sum+dfs(x,y+1))%mo; num[col]--; f[x][y]=record; } } return sum%mo; } signed main() { n=read();m=read();k=read(); if (n+m>k+1) { puts("0"); return 0;} for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) mp[i][j]=read(),num[mp[i][j]]++; memset(f,0,sizeof(f)); int tmp=dfs(1,1); printf("%lld\n",tmp%mo); return 0; }


