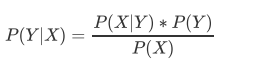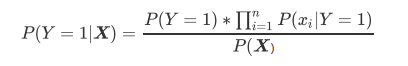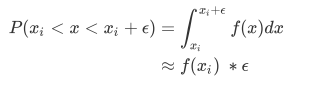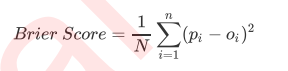机器学习-朴素贝叶斯
概率分类器:
- 朴素贝叶斯是一种直接衡量标签和特征质检的概率关系的有监督学习算法, 是一种专注分类的算法, 朴素贝叶斯的算法根源是基于概率论和数理统计的贝叶斯理论, 因此它是根正苗红的概率模型.
关键概念:
- 联合概率: X取值为x和Y的取值为y, 两个事件同时发生的概率, 表示为: P(X=x, Y=y)
- 条件概率: 在X取值为x的前提下, Y取值为y的概率, 表示为P(Y=y|X=x)
- 在概率论中, 我们可以证明, 两个事件的联合概率等于这两个事件任意条件概率*这个条件事件本身的概率
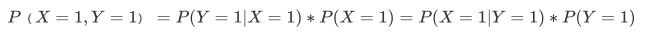
- 简单一些, 则可以将上面的式子写成:
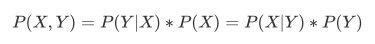
- 由上面的式子, 我们可以得到贝叶斯理论等式:
- 而这个式子,就是我们一切贝叶斯算法的根源理论, 我们可以把我们得的特征X当成是我们的条件事件, 而我么要求解的Y标签, 当成是我们被满足条件后, 会被影响的结果, 而两者之间的概率关系就是P(Y|X), 这个概率在机器学习中, 被我们称之为后验概率, 即是说我们先知道了条件, 再去求结果, 而标签Y在没有任何条件限制下取值为某个值的概率, 被我们写作P(Y), 于后验概率相反, 这是完全没有任何条件限制的, 标签的先验概率, 而我们的P(X|Y)被称为"类的条件概率", 表示当Y的取值固定的时候, X为某个值的概率.
在机器学习中:
- P(Y), 通常表示标签取到少数类的概率, 少数类往往使用正样本表示,也就是P(Y=1), 本质就是所有样本标签为1的样本所占的比例,
- 对于每一个样本而言:

- 对于分子而言, P(Y=1)就是少数类占总样本量的比例, P(X|Y=1)则需要稍微复杂一点的过程来求解
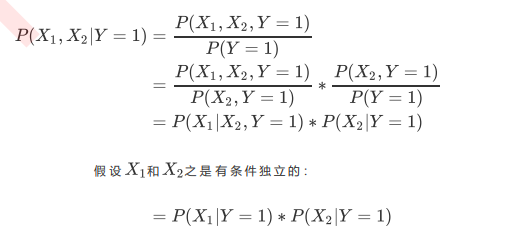
- 由此可知, 推广到n个特征来说:
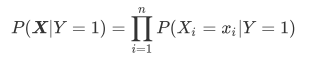
-
这个式子证明, 在Y=1的条件下, 多个特征的取值被同时取到的概率, 就等于Y=1的条件下, 多个特征的取值被分别取到的概率相乘., 其中假设X1,X2是有条件独立则可以让公式P(X1|X2, Y=1)=P(X1|Y=1), 这是在假设x2是一个对x1在某个条件下取值完全无影响的变量
- 假设特征之间是有条件独立的, 可以解决众多问题, 也简化了很多计算过程, 这是朴素贝叶斯被称为"朴素"的理由
- 我们贝叶斯理论等式的分母P(x), 我们可以使用全概率公式来求解P(X)
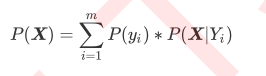
- 其中m代表标签的种类, 也就是说, 对于二分类来说:
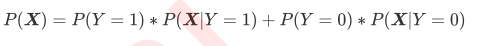
贝叶斯的性质与最大后验估计
- 朴素贝叶斯是一个不建模的算法, 朴素贝叶斯是第一个有监督, 不建模的分类算法
- 实际贝叶斯的决策过程:
- 对于一个二分类来说
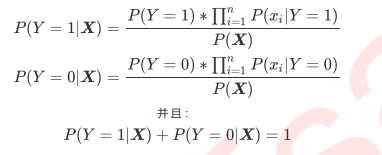
- 在分类的时候 我们选择P(Y=1|X)和P(Y=0|X)中较大的一个所对应的Y的取值, 作为这个样本的分类 在比较两个类别的时候, 两个概率计算的分母是一致的, 因此我们可以不用计算分母, 只考虑分子的大小, 当我们分别计算出分子的大小之后, 就可以通过让两个分子相加, 来获得分母的值, 以此来避免计算一个样本上所有特征下的概率P(X),这个过程, 被我们称为"最大喉炎估计"(MAP), 在最大后验估计中, 我们只需要求解分子, 主要是求解一个样本下每个特征取值下的概率P(xi|Y=yi), 再求连乘便能够获得响应的概率
- 当购买无数个汉堡的时候, 形成的细条曲线就叫做概率密度函数
- 一条曲线下的面积, 就是这条曲线所代表的函数的积分, 如果我们定义曲线可以用函数f(x)表示, 我们整条曲线下的面积就是:
- 其中dx是f(x)上的微分, 在某些特定的f(x)下, 饿哦们可以证明, 上述积分等于1, 总面积是1,, 这说明一个连续型特征X的取值x取到某个区间[xi, xi+ξ]之内的概率就为这个区间上概率密度曲线下的面积, 所以我们的特征Xi在区间[xi,xi+ξ]中取值的概率可以表示为
- 现在,我们呢就将求解连续型变量下某个点取值的概率问题没转化称了一个求解一个函数f(x)在点xi上的取值问题.
概率模型得评估指标
- 布里尔分数 Brier Score
- 概率预测得准确程度被称为"校准程度", 是衡量算法预测出得概率和真实结果得差异得一种方式, 一种比较常用得指标叫做布里尔分数, 它被计算为是概率预测相对于测试样本得均方误差, 表示为:
- 其中N是样本数量, pi为朴素贝叶斯预测出得概率, oi是样本所对应得真实结果, 只能取到0或者1, 如果事件发生则为1, 如果不发生则为0, 这个指标衡量了我们概率距离真实标签得结果得差异, 其实看起来非常想是均方误差, 布里尔分数得范围是从0到1, 分数越高, 则预测结果越差劲, 校准程度越差, 因此布里尔分数越接近0越好, 由于她得本质也是一种损失, 所在再sklearn中, 布里尔得分被命名为brier_score_loss.
- 概率预测得准确程度被称为"校准程度", 是衡量算法预测出得概率和真实结果得差异得一种方式, 一种比较常用得指标叫做布里尔分数, 它被计算为是概率预测相对于测试样本得均方误差, 表示为:
对数似然函数, LogLoss
- 另一种常用得概率损失衡量是对数损失(log_loss), 有叫做对数似然, 逻辑损失或者交叉损失, 它是多元逻辑回归以及一些拓展算法, 由于是损失, 因此对数似然函数得取值越小, 则证明概率估计越准确, 模型越理想, 值得注意得是, 对数损失只能用于评估分类型模型,对于一个样
本, 如果样本得真实标签y_true再{0,1}中取值, 并且这个样本再类别1得概率下, 概率估计为y_pred, 则这个样本得对应得岁数损失函数:
- 只不过在逻辑回归中得损失函数, 我们得真实标签是由yi表示, 预测值(概率估计)是由yθ(xi)来表示, 仅仅是表示的方式不同. 注意, 这里的log表示以e为底的自然对数
- 注意到, 我们用log_loss得出的结论和我们使用布里尔分数得出的结论不一致, 当使用布里尔分数作为评判标准的时候, svc的效果是最差的, 逻辑回归和贝叶斯的结果相近, 而是用似然对数的时候, 虽然再逻辑回归最强大, 但贝叶斯却没有svc的效果好. 那是因为逻辑回归和svc都是以最优化目的求解模型, 然后进行分类的算法, 而朴素贝叶斯却没有最优化的过程, 对数似然函数直接指向模型最优化方向, 甚至就是逻辑回归的损失函数本身, 因此在逻辑回归和svc上的表现的更好
选择对数似然还是布里尔分数参考下表:
| 需求 | 优先使用对数似然 | 有限使用布里尔分数 |
| 衡量模型 | 要对比多个模型, 或者衡量模型的不同变化 | 衡量单一模型 |
| 可解释性 | 机器学习和深度学习之间的行家交流,学术论文 | 商业报告, 老板开会, 业务模型的衡量 |
| 最优化问题 | 逻辑回归, svc | 朴素贝叶斯 |
| 数学问题 | 概率只能无限接近0或者1, 无法取到0或者1 | 概率可以取到0或者1, 比如树, 随机森林 |
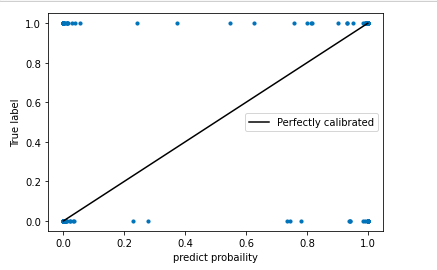
- 贝叶斯原理简单, 根本没有什么参数,但是产出概率的算法有自己的调节方式, 就是调节概率的校准程度, 校准程度越高,模型对概率的预测越准确, 算法再做判断时就越有自信, 模型就会越稳定,如果我们追求模型再概率上必须尽量贴近真实概率, 那我们就可以使用可靠性曲线来调节概率的校准程度
可靠性曲线:
- 可靠性曲线, 又叫做概率校准曲线, 可靠性图, 这是一条以预测概率为横坐标, 真实标签为纵坐标的曲线, 我们希望预测概率和真实值越接近越好, 最好两者相等, 因此一个模型/算法的概率校准曲线越靠近对角线越好, 因此校准曲线也是我们模型评估指标之一, 和布里尔分数相似, 概率校准曲线时对于标签某一类来说的, 因此一类标签就会有一条曲线, 或者我们可以使用一个多类标签下的平均来表示一整个模型的概率校准曲线, 但通常来说, 曲线用于二分类的情况很多.
- 绘制可靠性曲线, 纵坐标时标签, 但是我们绘制出来以后, 图像杂乱无章
- 因此, 我恩希望预测概率很靠近真实值, 那我们的真实取值必然也是需要一个概率才可以, 而真实标签额概率时不可获取的, 所以, 一个简单的做法时, 将数据进行分箱, 然后规定每个箱子中真实的少数类所占的比例为每个箱子上的真实概率trueproba, 这个箱子中预测概率的均值为这个箱子的预测概率predproba, 然后以trueproba为纵坐标, predproba为横坐标, 来绘制我们的可靠性曲线
- 对于贝叶斯, 如果概率校准曲线呈现sigmoid函数耳朵镜像情况, 则说明数据集中的特征不是相互条件独立,
- 支持向量机得概率校准曲线效果其实时典型得置信度不足得分类器得表现, 大量得样本点集中在决策边界附近, 因此许多样本点得置信度靠近0.5左右, 即便决策边界能够将样本点判断正确, 模型本身对这个结果也不是非常确信得, 相对的, 离决策边界很远得点得置信度就会很高, 因为她很大可能性上不会被判断错误, 支持向量机在面对混合度较高得数据得时候, 有着天生得置信度不足得缺点.
预测概率直方图:
- 概率密度曲线和概率分布直方图
- 概率密度曲线: 横坐标是样本得取值, 纵坐标时落在这个样本区间中得样本得个数, 衡量得每个X得取值区间之内有多少个样本, 服从高斯分布的X的取值上的样本的分布
- 概率分布直方图: 横坐标时概率的取值[0,1], 纵坐标是落在这个概率取值范围中的样本个数, 衡量的时每个概率取值区间之内有多少样本, 这个分布, 时没有任何假设的
校准可靠性曲线:
- 概率校正对于原本可靠性曲线是形容sigmoid形状的曲线的算法比较有效
多项式朴素贝叶斯:
- 多项式分布擅长的分类型变量, 在现实中,我饿们处理连续型变量, 通常会使用高斯朴素贝叶斯
- 多项式实验中的实验结果都很具体, 它所涉及的特征往往是次数, 频率, 计数, 出现与否这样的概念, 这些概念都是离散的正整数, 因此sklearn中的多项式朴素贝叶斯不接受负值的输入
- 由于这样的特性, 多项式朴素贝叶斯的特征矩阵经常是稀疏矩阵(不一定总是稀疏矩阵), 并且它经常被用于文本分类, 我们可以使用著名的TF-IDF向量技术, 也可以使用常见并且简单的单词技术向量, 手段于贝叶斯配合使用, 着两种手段属于常见的文本特征提取的方式,从数学角度来看, 在一种标签类别Y=c下, 我们有一组分别对于特征的参数向量θc = (θc1, θc2,...,θcn)其中n表示特征的总数, 一个θci表示这个标签类别下的第i个特征所对应的参数, 这个参数被我们定义为:
- 记作P(Xi|Y=c), 表示当Y=c这个条件固定的时候, 一组样本在Xi这个特征上的取值被取到的概率, 注意我们在高斯朴素贝叶斯中求解的概率P(xi|Y)是对于一个样本来说, 而我们现在求解P(Xi|Y=c)是对于一个特征Xi来说的概率, 对于一个在标签类别Y=c下, 结构为(m,n)的特征矩阵来说, 我们有:

- 其中每个xij都是特征Xi发生的次数, 基于这些理解, 我们可以通过平滑后最大似然估计来求解参数θy
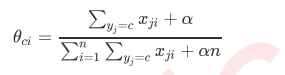
- 对于每个特征Σyj=c, xji是特征下所有标签的样本的特征取值之和, 其实就是特征矩阵中每一列的和. Σmi=1Σyj=cxji是所有标签类别为c的样本上, 所有特征的取值之和, 其实就是特征矩阵Xy中所有元素的和, α被称为平滑系数, 我们令α>0, 来防止训练数据中出现过的一些词汇没有出现在测试集中导致的0概率, 以避免让参数θ为0的情况, 如果我们设置为1, 则这个平滑叫做拉普拉斯平滑, 如果α小于1, 则我们把它叫做利德思通平滑, 两种平滑都属于自然语言处理中比较常用的用来分类数据的统计手段
伯努利朴素贝叶斯:
- 多项式朴素贝叶斯可同时处理二项式分布和多项式分布, 其中二项分布又叫做伯努利分布, 它是一种现实中常见, 并且拥有很多优越数学性质得分布, 因此, 既然有着多项式朴素贝叶斯, 我们自然也就有专门用来处理二项分布得朴素贝叶斯: 伯努利朴素贝叶斯
- 伯努利朴素贝叶斯类BernoulliN假设数据服从伯努利分布, 并在次基础上应用朴素贝叶斯得训练和分类过程, 多元伯努利分布简单来说,就是数据集中可以存在多个特征, 但每个特征都是二分类得, 可以以布里尔变量表示, 也可以表示为{0,1}或者{-1,1}等任意二分类组合, 因此,这个类要求将样本转换为二分类特征向量, 如果数据本身不是二分类得, 那就可以是有那个类中专门用来二值化得参数binarize来改变数据, 伯努利朴素贝叶斯UI多项式朴素贝叶斯非常相似, 都常用于处理文本分类, 但是由于伯努利朴素贝叶斯是处理二项分布得, 所以它更加在意"存在与否", 而不是"出现多少次"这样得次数或频率, 这是伯努利贝叶斯于多项式朴素贝叶斯得根本不同, 在文本分类得情况下, 伯努利朴素贝叶斯可以使用单词出现向量(而不是单词计数向量)来训练分类器, 文档较短得数据集上, 伯努利朴素贝叶斯效果会更加好.
补集朴素贝叶斯
- TF-IDF: 我们使用单词在句子中所占的比例来编码我们的单词, 就是我们著名的TF-IDF方法, 是通过单词在文档中出现的频率来衡量其权重, ,也就是说, IDF的大小于一个词的常见程度成反比, 这个词月常见, 编码后为它设置的权重会倾向于越小, 以此老压制频繁出现的一些无意义的词.