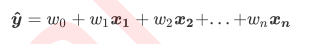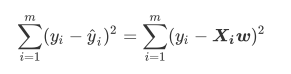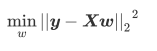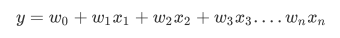机器学习-线性回归大家族
回归是一种应用广泛的预测建模技术, 这种技术的核心在于预测的结果是连续型变量
通常理解线性代数可以有两种角度:矩阵的角度喝代数的角度, 几乎所有的机器学习的教材都是从线性代数角度来理解线性回归, 类似于逻辑回归喝支持向量机, 将求解参数的问题转化为一个带条件的最优化问题, 然后用三维图像让大家求极值的过程
线性回归是机器学习最简单的回归算法, 多元线性回归指的是一个样本有多个特征的线性回归问题, 对于有n个样本特征而言, 他的回归结果可以写作

- w被统称为模型的参数, 其中w0被称为截距, w1~wn被称为回归系数, 有时也是使用θ或者β来表示, 其中y是我们目标变量, 也就是标签, , xi1~xin是样本i上的不同特征, 如果考虑我们有m个样本, 则回归结果可写作:
- 线性回归的任务, 就是构造一个预测函数来映射输入的特征矩阵X喝标签值y的线性关系, 这个预测函数在不同的教材上写法不同, 科恩那个写作f(x), y(x), 或者h(x)等等的形式, 但无论如何, 这个预测函数的本质就是我们需要构建的模型, 而构造预测模型的核心就是找出模型的参数向量w, 在多元线性回归中, 我们的损失函数如下定义:
- 其中yi是样本i对应的真实标签, yi'也就是Xiw是样本i在一组参数w下的预测标签, 首先,这个损失函数代表了向量y-y'的L2范式的平方的结果, L2范式的本质就是欧式距离, 即使两个向量的么哦个点对应相减后的平方和, 并没有开方, 所以我们的损失函数是L2范式, 即欧式距离的平方结果
- 在这个平方结果下, 我们的y和y'分别是我们的这是标签喝预测值, 也就是说, 这个损失函数实在计算我们的真实标签喝预测值之间的距离, 因此, 我们认为这个损失函数衡量了我们构造的模型的预测结果喝真实标签的差异, 因此我们固然希望我们的预测结果喝真实值差异越小越好, 所以我们的求解目标就可以转化为:
- 其中右下角的2表示向量y-Xw的L2范式, 也就是我们损失函数所代表的含义, 在L2范式上开平方, 就是我们的损失函数, 这个式子, 在sklearn中, 用在类Linear.LonerRehression背后使用的损失函数, 我们往往称这个式子为SSE(误差平方和), 或者RSS(残差平方和)在sklearn我们称之为RSS残差平方和.
最小二乘法求解多元线性回归参数
- 现在问题转换成了求解让RSS最小化的参数向量, 这种通过最小化真实值喝预测值质检的RSS来求解参数的方法叫做最小二乘法, 求解极值的第一步往往是求解一阶导数, 并让一阶导数等于0, 最小二乘法也不能免俗, 因此, 我们在残差平方和RSS上对参数向量w求导


- 到这里, 我们希望能够讲w留在等式的左边, 其他特征矩阵有关的部分都放到右边, 如此就可以求出w的最优解了, 这个功能非常容易实现, 只需要做乘XTX的逆矩阵就可以了, 在这里, 逆矩阵存在的充分必要条件是特征不存在多重共线性
| 参数 | 含义 |
|
fit_intercept_ |
布尔值, 可不填, 默认是True, 是否计算此模型的截距, 如果设置为False, 则不会计算截距 |
| normalize |
布尔值, 可不填, 默认为False, 当fit_intercept设置为False时, 将忽略此参数, 如果为True, 则特征矩阵x进入回顾之前将回被减去均值(中心化)并除以L2范式(缩放) 如果你希望进行标准化, 请在fit数据之前使用preprocessing模块中的标准化专用类StandardScaler |
| copy_x |
布尔值, 可不填, 默认是True 如果为True, 将在copy()上进行操作, 否则的话原本的特征矩阵x可能被线性回归影响并覆盖 |
| n_jobs |
整数或者None,可不填, 默认为True, 用于计算的作业数, 只在多标签的回归中和数据量足够大的时候才生效, .除非None在joblibparallel_backend上下文中, 否则None 统一表示为1, 如果输入-1, 则表示使用求俺不的cpu来进行计算 |
线性回归的属性
| 属性 |
含义 |
| coef_ |
数组, 形状为(n_features)或者(n_targets, nfeatures), 线性回归方程中, 估计出的系数, 如果在fit中传递多个标签(当y为二维活以上的时候), 则返回 的系数是形状为(n_target, n_features)的二维数组, 二如果仅传递一个标签, 则返回的系数是长度为n_features的一组数组 |
|
intercept_ |
数组, 线性回归中的截距项 |
回归类模型的评估指标
- 回归类算法的模型评估一致都是回归算法中的一个难点, 但不像我们曾经讲过的无监督学习算法中的轮廓系数等等评估指标, 回归类与分类型算法模型评估其实是相似的法则, 找真实标签和预测的差异, 只不过在分类算法总, 这个差异只有一种角度来评判, 那就是是否预测了正确的分类, 而在我们回归类算法中, 我们有两种不同的角度看待回归的效果
- 我们是否预测到了正确的数值
- RSS是我们的残差平方和, 它的本质是我们预测值与真实值之间的差异, 也就是从第一种角度来评估我们回归的效力, 所以RSS即是我们的损失函数, 也是我们回归模型的评估指标之一, 但是, RSS有这致命的缺点: 它是一个无界的和, 可以无限的大, , 从RSS的公式看, 他不能为负, 所以越接近0越好, 但是, 究竟多小才好呢?应对这种状况, 我们使用均方误差MSE来衡量我们的预测值和真实值的差异
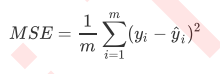
- 均方误差本质是在RSS的基础上除以样本总量, 得到每个样本量上的平均误差, 有了平均误差, 我们就可以将平均误差和我们的标签取值范围在一起比较, 以此获得一个较可靠的依据, 我们有两种方式调用这个评估指标, 一种是使用sklearn专用的模型评估metric里的类mean_squared_error, 另一种是调用交叉验证的类cross_val_score并使用里面的sciring参数来设置使用均方误差
- 均方误差为负:
- 这是因为在sklearn计算模型评估指标的时候, 回考虑指标本身的性质, 均方误差本身是一种误差, 所以被sklearn划分为模型的一种损失, 在sklearn的损失都使用负数表示, 因此均方差误差也被显示为负数了, 真正的均方误差MSE的数值, 其实是neg_mean_squared_error去掉符号的数字
- 除了了MSE,我们还有与MSE类似的MAE绝对值误差
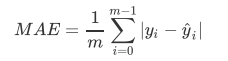
- 其表达的概念与均方误差完全一致, 不过在真实标签和预测值之间差异外, 我们使用的是L1范式(绝对值). 现实使用中, MSE和MAE选一个来使用就好了
- 我们是否拟合到了足够的信息
- 方差能判断预测的数值是否正确, 不能够判断我们的模型是否拟合了足够多的, 数值之外的信息
- 在我们学习姜维算法PCA的时候, 我们提到是有那个方差来衡量数据上的信息量, 如果方差越大, 代表数据上的信息量越多, 而这个信息量不仅包括数值的大小, 还包括我们希望模型捕捉的哪些规律, 为了衡量模型对数据上的信息量的捕捉, 我们定义R2
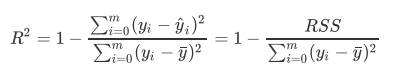
- 分子误差, 分母是方差, 方差的本质是任意一个y值和样本均值的差异, 差异越大, 这些值所带信息越多, 在R2中, 分子是真实值和预测值的差值, 也就是我们的模型没有捕获到的信息总量, 分母是真实标签所带信息量, 所以其衡量的是1-我们模型没有捕获到的信息量占真实标签中所带的信息量的比例, 所以R2越接近1越好
- 负的R2, :
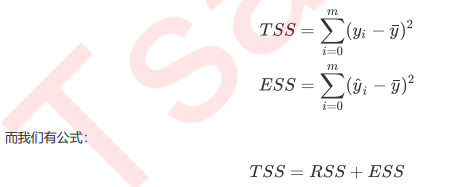

- 因为TSS = RSS + ESS不是永远都成立的,
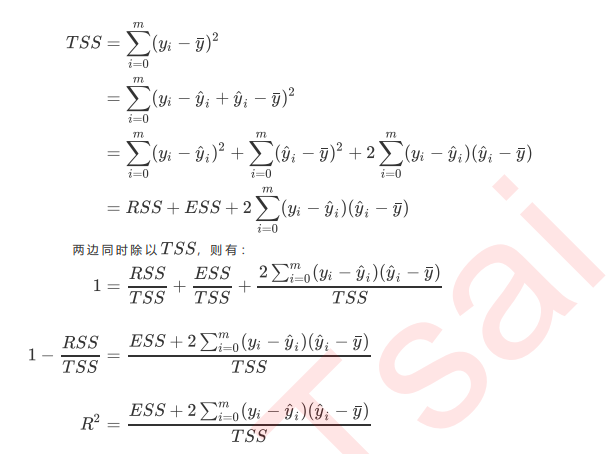
多重共线行: 岭回归与Lasso
- 我们推导多元线性回归是有那个最小二乘法的求解原理
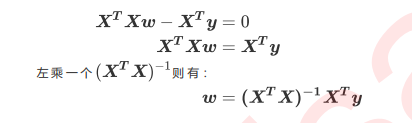
- 逆矩阵存在的充分必要条件是特征矩阵不存在多重共线性,
- 逆矩阵的计算公式
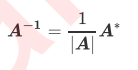
- 分子上A*是伴随矩阵, 任何矩阵都可以有伴随矩阵, 因此这一部分不影响矩阵的存在性, 二分母上的行列式|A|就不同了, 位于分母的变量不为0, 一旦为0则无法计算出逆矩阵, 因此逆矩阵存在的充分必要条件: 矩阵的行列式不能为0, 对于线性回归而言, 也就是说|XTX|不能为0, 这是使用最小二乘法求接线性回归的核心条件之一
- 满秩矩阵:
- A是一二n行n列的矩阵 若A转换为提醒矩阵后, 没有任何全为0的或者全为0的列, 则称A为满秩矩阵, 简单来说, 只要对角线上没有一个元素为0, 则这个矩阵中绝对不可能存在全为0的行或者列
- 即是说, 矩阵满秩(即转换为梯形矩阵后对角线上没有0)是矩阵的行列式不为0的充分必要条件
- 造成模型有偏差或者不同, 精确相关关系和高度相关关系并称为多重共线性
- 一个矩阵如果要满秩, 则要求矩阵中每个向量之间不能存在多重共线性, 这也是构成了线性回归算法对于特征矩阵的要求
- 多重共线行如果存在, 则线性回归就无法使用最小二乘法来进行求解, 或者求解会出现偏差, 幸运的是, 不能存在多重共线性, 不代表不能存在相关性--机器学习不要求特征之间必须独立, 不洗不相关, 只要不是高度相关或者精确相关就好
- 多重共线性: 是一种统计现象, 是指线性模型中的特征(解释变量)之间由于存在精确相关关系, 多重共线的存在回使模型无法建立, 或者估计失真, 多重共线行使用指标方差膨胀因子来进行衡量,通常我们推导共线行, 都特指多重共线性
- 相关性是衡量两个或多个变量一起波动的程度指标, 它可以是正的, 负的, 或者0, 当我们说变量之间具有相关性, 通常是指线性相关, 线性相关一般由皮尔逊相关系数进行衡量, 非线性相关剋使用斯皮尔曼相关系数或者互信息法进行衡量
岭回归:
- 岭回归在多元线性回归的损失函数加上正则项, 表达为系数w的L2范式(即系数w的平方和)乘以正则化系数α.所以岭回归的损失函数的完整表达式:
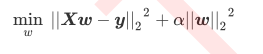


- α等于0,
- 原本的矩阵XTX中存在对角线上元素为-α, 其他元素都为0的行或者列
- 岭回归和Lasso不是设计来提升模型表现, 而是专注于解决多重共线性问题的, 但当α在一定范围内变动的时候, 消除多重共线行也许能后一定程度上提高模型的泛化能力
| 重要参数 | 含义 |
| alphas | 需要测试的正则化参数的取值的元祖 |
| scoring | 用来进行交叉验证的模型评估指标, 默认是R2, 可自行调整 |
| store_cv_values | 是否保存每次交叉验证的结果, 默认是False |
| cv |
交叉验证的模式, 默认是None, 表示默认进行留一交叉验证, 可以输入Kfold对象, 和StratifiedKFold对象来进行交叉验证,注意: 仅仅当为None时, 每次交叉验证的结果 才可以被保存下来, 当cv有值存在(不是None)时, store_cv_values无法被设定为True |
| 重要属性 | 含义 |
| alpha_ |
查看交叉验证选中的alpha |
| cv_values_ | 调用所有交叉验证的结果, 只有当store_cv_values=True的时候才能调用, 因此返回的结构是(n_samples, n_alphas) |
| 重要接口 | 含义 |
| score | 调用Ridge类不行静交叉验证的情况下返回的R平方 |
Lasso于多重共线性:
- Lasso全称最小据对收缩和选择算子, 和岭回归一样, Lasso时被创造来作用于多重共线性问题的算法, 不过Lasso使用的时系数w的L1范式(L1范式这是系数w的绝对值)乘以正则化系数α, 所以Lasso的损失函数为:
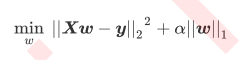

- 我们在L1范式所带的正则项α在求导之后, 并不带有w这个项, 因此无法对XTX造成任何影响, 因此, Lasso五大解决特征之间的"精确相关的问题"
- 岭回归 VS Lasso
- 岭回归可以解决特征质检的精确相关关系导致的最小二乘法无法使用的问题, 而Lasso不行
- Lasso不是从根本上截距多重共线性问题, 二hi限制多重共线性带来的影响, 因为Lasso采用的L1正则化, , 会将贡献不大的特征压缩为0, 这个性质让Lasso成为线性模型中的特征选择工具首选.
正则化路径
- 假设我们的特征矩阵中有n个特征, 则我们就有特征向量x1, x2, ...xn对于每一个α的取值, 我们都可以得出一组对应这个特征向量的参数向量w,其中包含了n+1个参数, 分别好似w0, w1,w2...wn,这些参数可以被看做是一个n+1维空间中的一个点(想想我们在猪成分分析和奇异值分解中讲解的n维空间)对于不同的α取值, 我们就将得到许多个在n+1维空间的点, 所有的这些点的序列, 就被我们称之为正则化路径, 我们把这个正则化路径的α最小值除以α的最大值的量αmax/αmin称为正则化路径的长度
| 参数 | 含义 |
| eps | 正则化路径的长度, 默认是0.001 |
| n_samples | 正则化路径中α的个数, 默认是100 |
| alphas | 需要测试的正则化参数的取值的元组, 默认是None, 当不输入的时候, 自动使用eps和n_alphas来自动生成带交叉验证的正则化参数 |
| cv | 交叉验证的次数, 默认3折交叉验证 |
| 属性 | 含义 |
| alpha_ | 调用交叉验证选出来的最佳正则化参数 |
| alphas_ | 使用正则化路径的长度和路径中α的个数来自动生成的, 用来进行交叉验证的正则化参数 |
| mse_path | 返回所以交叉验证的结果细节 |
| coef_ | 调用最佳正则化参数下建立模型的系数 |
非线性问题: 多项式回归
- 线性这个洗用于描述不同事物有着不认同的含义, 我们最常用的线性是指变量之间的线性关系, 他表示两个变量质检的关系可以展示为一条直线
- 线性数据: 通常来说, 一组数据由多个特征和标签组成, 当这些特征分别于标签存在线性关系的时候, 我们就说这一组数据是线性数据
- 非线性数据: 当特征矩阵中任意一个特征与标签质检的关系需要使用三角函数, 指数函数来定义, 则我们说这种数据叫做非线性数据
- 总之:
- 对于回归问题, 数据若能分布为一条直线, 这是线性的,否则是非线性的
- 对于分类问题, 数据分布若能使用一条直线来划分类别, 则是线性可分的, 否则数据则是线性不可分的
- 在回归中,线性数据可以是有那个如下的方程来拟合:
- 也就是我们的线性回归方程, 根据线性回归的方程, 我们可以拟合出一组参数w, 在每一组固定的参数下, 我们可以建立一个模型, 而这个模型就被我们称之为线性回归模型, 所以建模的过程就是寻找参数的过程, 此时此刻我们建立的线性回归模型, 是一个用于拟合线性数据的线性模型, 作为线性模型的典型代表, 我么美女可以从线性回归的方程中: 自变量都是一次项
- 线性模型可以用来拟合非线性数据, 而非线性模型也可以用来拟合线性数据, 更神奇的是, 有的算法没有模型也可以处理各类数据, 而有的模型既可以是线性, 也可以是非线性
- 线性模型的决策边界是平行的直线, 飞线性模型的决策边界是曲线或者交叉的直线
多项式变化:
- 这是一种通过增加自变量上的次数, 而将数据映射到高维空间的方法, 只要我们设定一个自变量上的次数(大于1), 就可以相应地获得数据投影在高次方地空间中地结果,
- 多项式回归转化次数是n, 则数据回被转化成:
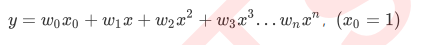
- 这就是大家会在大多数机器学习教材中看到地多项式回归地表达式, 上述是我们讲一维数据升维, 那如果是多维数据升维呢?
- 二项式

- 三项式

- 不难发现:当我们进行多项式转换地时候, 多项式会产生到最高次数为止地所有低高次项, 比如如果我们规定多项式地次数为2, 多项式就会产出所有次数为1和次数为2的项反馈给我们, 相应地如果我们如果规定多项式地次数为n, 则多项式会产出所有次数为1到次数为n地项, 注意, x1x2和x12一样都是二次项, 一个自变量地平方其实也就相当于是x1x1, 所以三次项多项式中x12x2就是三次项
- 在多项式回归中, 我们可以规定是否产生平方或者立方项, 其实如果我们只要求高次项地话, x1x2会是一个比x12更好地高次项, 因为x1x2和x1之间地共线性会比x12和x1之间地共线性好那么一点点(只是一点点), 而我么多项式转化后是需要使用线性回归模型来拟合的, 就算机器学习中不是那么在意数据上地基本假设, 但是太过分地共线性还是会影响模型地拟合.
- 随着原特征矩阵维度地上升, 随着我么规定地次数地上升, 数据会变的越来越复杂, 维度越来越多, 并且这种维度地增加并不能用太简单地数学公式表达出来, 因此, 多项式回归没有固定地模型表达式,多项式回归地模型最终长什么样子是由数据和最高次数决定, 因此我们无法断言说某个数学表达式就是多项式回归地数学表达式
狭义线性模型VS广义线性模型
- 狭义线性模型: 自变量不能有高次项,自变量于标签之间不能存在非线性关系
- 广义线性模型: 只要标签与模型拟合出的参数之间地关系是线性的, 模型就是线性地, 这是说, 只要生成地一系列w之间没有相乘或者相除地关系, 我们认为模型是线性
- 多项式回归通常被认为是非线性模型, 但广义上是一种特殊的线性模型, 它能够帮助我们处理非线性数据, 是线性回归的一种进化.