机器学习-聚类KMeans
无监督学习-聚类算法
- 聚类算法有焦作"无监督分类", 其目的是将数据阿虎分成有意义或有用的组(簇).
| 聚类 | 分类 | |
| 核心 | 将数据分成多个组, 探索每个组的数据是否有联系 | 从已经分组的数据中取学习, 把新数据放到已经分好的组中去 |
| 学习类型 | 无监督, 无需标签进行训练 | 有监督, 需要标签进行训练 |
| 典型算法 | K-Means, DBSCAN, 层次聚类, 光谱聚类 | 决策树, 贝叶斯, 逻辑回归 |
| 算法输出 |
聚类结果是不确定的, 不一定总是能够反映数据的真实分类 同样的聚类, 根据不同的业务需求, 可能是一个好结果, 也可能是一个坏结果 |
分类结果是确定的, 分类的优劣是客观的, 不是根据业务或算法需求确定 |
簇和质心:
- 簇: KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇, 直观上来看是簇一组一组聚集在一起的数据, 在一个簇中的数据就认为是同一类, 簇就是聚类的结果表现
- 质心: 簇中所有数据的均值μj通常被称为簇的质心(centroids)没在一个二维平面中, 一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值, 质心的纵坐标就是这一簇数据点的纵坐标的均值, 同理可推广至高维空间
聚类过程:
- 随机抽取K个样本作为最初的质心
- 开始循环,
- 将每个样本点分配到离它们最近的质心, 生成k个簇
- 对于每个簇, 计算所有被分配到该处的样本点的平均值作为新的质心
- 当质心的位置不在发生变化, 迭代停止, 聚类完成
- PS: 当我们找到一个质心, 在每次迭代中被分配到这个质心上的样本都是一致的, 即每次新生成的簇都是一致的, 所有样本点都不会在从一个簇转移到另一个簇, 质心就不会变化了
簇内误差平方和
- 我们认为, 被分在同一个簇中的数据是有相似性的, 而不同簇中的数据是不同的, 聚类算法中, 我们追求"簇内差异小, 簇外差异大", 而这个差异, 有样本点到其所在簇的质心的距离来衡量, 对于一个簇没所有样本点到质心的巨鹿之和越小, 我焖就认为,这个簇中样本越相似, 簇内差异越小, 而距离的衡量方法有多重, 令x表示簇中的一个样本点, μ表示该簇中的质心, n表示每个样本点的特征数目, i表示组成点x的每个特征, 则样本点到质心的距离可以由以下距离来衡量:

- 如果我们采用欧几里得距离计算, 那么一个卒中所有样本点的距离之和为:

- 其中m为一个簇中的个数, j是每个样本的编号, 这个公式被称为簇内平方和, 又叫做Inertia, 而将一个数据集中所有的簇耳朵簇内平方和相加, 就得到了整体平方和, 又叫作total intertia, Total Inertia越小, 代表每个簇内样本越相似, 胡磊的效果越好, 因此KMeans追求的是, 求解能够让Intertia最小化的质心, 实际上,在质心不断变化不断迭代的过程中, 总体平方和是越来越小的, 当整体平方和最小的时候, 质心就不在发生变化了
| 距离度量 | 质心 | Inertia |
| 欧几里得距离 | 均值 | 最小化每个样本点到质心的欧式距离之和 |
| 曼哈顿距离 | 中位数 | 最小化每个样本点到质心的曼哈顿距离之和 |
| 余弦距离 | 均值 | 最小化每个样本点到质心的余弦距离之和 |
KMeans算法的时间复杂度:
- 除了模型本身的效果之外, 我焖还是用另一种角度衡量算法: 算法复杂度, 算法的复杂度分为时间复杂度和空间复杂度,
- 时间复杂度: 是指执行算法所需要的计算工作量时间, 常用大O符号来表示,
- 空间复杂度: 是指这个算法所需要的内存空间
- KMeans算法的平均复杂度是O(K*n*T), 其中K是我们的超参数, 所需要输入的簇数, n是整个数据集中的样本量, T是所需要的迭代次数(相对的, KNN的平均复杂度是O(n)).
重要参数n_clusters
- n_clusters是KMeans中的k,也就是我们分簇的个数
聚类算法的模型评估指标
- 当真实标签已知的时候
| 模型评估指标 | 说明 |
|
互信息分 普通互信息分 metrics.adjusted_mutial_info_score(y_pred, y_true) 调整互信息分 metrics.mutual_info_score(y_pred, y_true) 标准化互信息分 metrics.narmalized_mutual_info_score(y_pred, y_true) |
取值范围在(0,1)之中, 越接近1, 聚类效果越好, 在随机均匀聚类下,产生0分 |
|
V-measure: 基于条件的一系列直观度量 同质性: 是否每个簇仅包含单个类的样本 metrics.homogeneity_score(y_true, y_pred) 完整性: 是否给定类的所有样本都被分配给同一个簇中 metrics.completeness_score(y_true, y_pred) 同质性和完整性的调和平均, 叫做V-measure metrics.v_measure_score(labels_true, labels_pred) 三者可以被一次性计算出来 metrics.homogeneity_completeness_v_measure(labels_true, labels_pred) |
取值范围在(0,1)之中, 越接近1, 聚类效果越好, 由于分为同质性和完整性两种度量, 可以更仔细地研究, 模型到底那个任务做的不好 对样本分布没有假设, 在任何分布上都可以又不错的表现, 在随机均匀聚类下不会产生0分 |
|
调整兰德系数 metrics.adjusted_rand_score(y_true, y_pred) |
取值在(-1,1)之间, 负值象征这簇内的点差异巨大, 甚至相互独立, 正类的兰德系数比较优秀, 越接近1越好 对样本分布没有假设, 在任何分布上都可以又不错的表现, 尤其是具有"折叠"形状的数据上表现优秀, 在随机均匀聚类下产生0分 |
- 当真实标签未知的情况下
- 评价聚类算法指标(簇内差异小, 簇外差异大): 轮廓系数是最常用的聚类算法的评价指标, 它是对于每个样本来定义的, 它能够同时衡量:
- 样本与其自身所在的簇中的其他样本形似度a, 等于样本与同一簇中所有其他店之间的平均距离
- 样本与其他簇中的样本的相似度b, 等于样本与下一个最近簇中的所有点之间的平均距离
- 单个样本得轮廓系数:
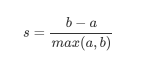
- 这个公式可以解析为:
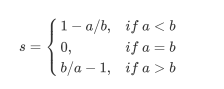
- 所以很容易理解, 轮廓系数得范围是(-1,1), 其中值越接近1表示样本与自己所在得簇中得样本很相似, 并且与其他簇中得样本不相似, 当样本点与簇外得样本更相似得时候, 轮廓系数就胃负, 当轮廓系数为0时 则代表两个簇中得样本相似度一致, 两个簇本应该是以个簇
- 如果一个簇中得大多数样本具有比较高的轮廓系数, 则簇会有比较高得总轮廓系数, 则整个数据集得平均轮廓系数越高, 则聚类是合适的, 如果许多样本点具有低轮廓系数甚至负值, 则聚类是不合适的, 聚类的超参数k可能设定的太小或太大
- 评价聚类算法指标(簇内差异小, 簇外差异大): 轮廓系数是最常用的聚类算法的评价指标, 它是对于每个样本来定义的, 它能够同时衡量:
- 当真实标签未知的情况下:
- 除了轮廓系数是最常用的, 还有卡林斯基-哈拉巴斯指数(方差比标准), 戴维斯-布尔丁指数以及权变矩阵
- 卡林斯基-哈拉巴斯指数
- sklean.metrics.calinski_harabaz_score(x, y_pred)
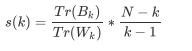
- 其中N为数据集中的样本量, k为簇的个数(即类别的个数), BK是组件离散矩阵, 即不同簇之间的协方差矩阵, Wk是簇内离散矩阵, 即一个簇内数据的协方差矩阵, 而tr表示矩阵的迹, 在线性代数中, 一个nxn矩阵的主对角线(从左上方至右下方的对角线)上各个元素总和被称为矩阵A的迹, 一般记作tr(A), 数据之间的离散程度越高, 协方差矩阵的迹就会越大, 组内离散程度低, 协方差的迹就会越小, Tr(Wk)也就越小, 同时,组间离散程度大, 协方差的迹也会越大, TT(Bk)就越大, 这正是我们希望的, 因此越高越好
- 戴维斯-布尔丁指数
- sklearn.metrics.davies_bouldin_score(x, y_pred)
- 权变矩阵
- sklearn.metrics.cluster.contingency_matrix(x, y_pred)
重要参数init & random_state & n_init
- 初始质心放置的位置不同, 聚类的结果很可能也会不一样.
重要参数max_iter & tol: 让迭代停下来
- 当质心不在移动的时候, KMeans算法就会停下来, 但在完全收敛之前, 我们可以使用max_iter, 最大迭代次数, 或者tol, 两次迭代间intertia下降的量小于tol的值.迭代就提前停下来,
重要属性与重要接口
- 属性:
| cluster_centers_ | 收敛到的质心, 如果算法在完全收敛之前就已经听下了,(受到参数max_iter和tol的控制), 所返回的内容将与labels_属性中反映出来的聚类结果不一致 |
| labels_ | 每个样本点对应的标签 |
| inertia_ | 每个样本点到距离它们最近的簇心的俊方距离, 有叫做簇内平方和 |
| n_iter_ | 实际的迭代次数 |
| fit | 训练特征矩阵X[训练使用标签, sample_weight] | 拟合模型, 计算K均值的聚类结果 |
| fit_predict | 训练特征矩阵X[训练使用标签, sample_weight] | 返回每个样本所对用的簇的索引, 计算质心并且为每个堂本预测所在的簇的索引, 功能相当于限fit,再predict |
| fit_transform | 训练特征矩阵x[训练用标签, samole_weight] | 返回新空间中的特征矩阵, 进行聚类并且将特征矩阵x转换到簇距离空间当中, 功能相当于先fit再transform |
| get_params | 不需要任何输入 | 获取该类的参数 |
| predict | 测试特征矩阵x[sample_weight] |
预测每个测试集x的样本所在的簇, 并返回每个样本所对应的簇的索引,在矢量画的相关文献中, cluster_centers_被称为代码薄, 而predict返回的咩个值是代码薄中最接近的代码的索引 |
| score | 此时特征矩阵x[训练用标签, sample_weight] | 返回聚类后的inertia,即村诶平方和的负数, 簇内平方和是KMeans常用的模型评价指标, 簇内平方和越小越好, 最佳值为0 |
| set_params | 需要新设定的参数 | 为建立好的类重设参数 |
| transform | 任意特征矩阵X |
将x转换到簇距离空间中, 在新空间中, 每个维度(即每个坐标轴)是样本点到集群中心的距离, 请注意, 即使x是稀疏的, 变换返回 的数组通常也是密集的 |
KMeans的矢量量化应用
- KMeans聚类的矢量量化本质是一种降维的运用, 但它跟我们之前学过的任何一种降维算法的思路都不同, 特征选择的降维是直接选取对模型贡献最大的特征, PCA的降维是聚合信息, 而矢量化的降维是在同等样本上的压缩信息的大小, 即不改变特征的数目, 也不改变样本的数目, 只改变在这些特征下样本上的信息量.
- K-Means聚类中获得质心来替代原有的数据, 可以把数据上的信息量压缩到非常小, 但又不损失太多信息.
KMeans参数列表
| n_clusters | 整数, 可不填, 默认是8, 要分成的簇数, 以及要生成的质心数 |
| init |
可输入'K-means++', "random"或是一个n为数组, 初始化质心的方法, 默认"K-means", 输入"K-means++": 一种为k均值聚类选择初始聚类中心的聪明的办法, 哟加速收敛, 详细信息请参阅k_init中注释的部分 如果输入了n维数组, 数组的形状应该是(n_clusters, features)并给出初始质心 |
| n_init | 整数, 默认10, 使用不认同的质心随机初始化种子来运行k-means算法的次数, 最终结果会是基于Inertia来计算n_init连续运行后的最佳输出 |
| max_iter | 整数, 默认300, 单词运行的k-means算法的最大迭代次数 |
| tol | 浮点数, 默认1e-4, 两次迭代件Inertia下降的量, 入股哦来那个词迭代之间Iertia下降的值小于tol所设定的值, 迭代就会停下来 |
| precompute_distances |
"auto", True, False,默认"auto" 预计算距离(更快但需要更多的内存) "auto": 如果(n_samples * n_nluster) > 1200万, 请不要余弦计算距离, 这相当于使用双精度来学习, 每个作业大约需要100MB的内存开销 True: 始终预先计算距离 False: 从不预先计算距离 |
| verbose | 整数, 默认是0, 计算中的详细模式 |
| random_state | 整数, RandomState或者None, 默认是None, 确定质心初始化的随机数生成, 使用init可以使随机性具有确定性 |
| copy_x |
布尔值, 可不填, 默认是True 在余弦计算距离时, 如果先中心化数据, 距离的预计算会更加精确, 如果copy_x为True(默认值), 则不修改原始数据, 确保特征矩阵X时C-连续(C-contiguous)的, 如果时False, 原始数据被修改, 并在函数返回之前放回, 但是可以通过减去货增加数据均值来引入微笑的数值差异, 在这种情况下, False模式去发确保数据C-时连续的, 这可能导致K-Means 的计算显著变慢 |
| n_jobs |
整数或None, 可不填, 默认是1 用于计算距离时, 如果先中心化数据, 距离的预计算互更加精确, 如果copy_x为True(默认值), 则不修改原始数据, 确保特征矩阵x是C-连续(C-contiguous)的, 入股为False, 原始数据被修改, 并在函数返回之前放回, 但是可以通过减去或增加数据均值来引入微笑的数值差异, 在这种情况下, False模式无法确保数据是C-连续的, 者可能导致K-Means的计算显著变慢 |
| algorithm |
可输入 "auto", "full" or "elkan", 默认为 "auto" K-means算法使用, 经典的EM风格算法是"完整的", 通过使用三角不等式, "elkan"变体更有效, 但目前不支持稀疏数据, "auto"为密集数据选择, "elkan"为稀疏数据选择"full" |



