Codeforces Round #Pi (Div. 2) (STL专场)
水题,拼手速。
/*
* @author Novicer
* language : C++/C
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
#include<iomanip>
#define INF 2147483647
#define cls(x) memset(x,0,sizeof(x))
#define rise(i,a,b) for(int i = a ; i <= b ; i++)
using namespace std;
const double eps(1e-8);
typedef long long lint;
const int maxn = 100000 + 5;
lint x[maxn];
int main(){
int n;
cin >> n;
for(int i = 1 ; i <= n ; i++)
scanf("%I64d",&x[i]);
sort(x+1,x+n+1);//事实上不用排序的:)
cout << x[2] - x[1] << " " << x[n] - x[1] << endl;
for(int i = 2 ; i < n ; i++){
lint mi = min(x[i] - x[i-1] , x[i+1] - x[i]);
lint ma = max(x[n] - x[i] , x[i] - x[1]);
printf("%I64d %I64d\n",mi,ma);
}
cout << x[n] - x[n-1] << " " << x[n] - x[1] << endl;
return 0;
}
B - Berland National Library
预处理一開始没出现过的“- x”,在开头补充“+ x"
然后用set模拟进入与离开的过程。输出最大的set容量。
/*
* @author Novicer
* language : C++/C
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
#include<iomanip>
#define INF 2147483647
#define cls(x) memset(x,0,sizeof(x))
#define rise(i,a,b) for(int i = a ; i <= b ; i++)
using namespace std;
const double eps(1e-8);
typedef long long lint;
bool vis[1000005];
int del[105],add[105],s[105];
set<int>lib;
int main(){
// freopen("input.txt","r",stdin);
int n;
cin >> n;
cls(vis);
cls(del);cls(add);cls(s);
int ans = 0;
int tmp;
int x = 0;
int ans1 = 0 , ans2 = 0;
for(int i = 1 ; i <= n ; i++){
char c;
cin >> c;
if(c == '+'){
cin >> add[i];
vis[add[i]] = true;
}
else{
int num;
cin >> num;
if(!vis[num]){
x++;
s[x] = num;
del[i] = num;
}
else{
del[i] = num;
}
}
}
for(int i = 1 ; i <= x ; i++) lib.insert(s[i]);
ans = lib.size();
for(int i = 1 ; i <= n ; i++){
if(add[i] != 0){
lib.insert(add[i]);
}
else if(del[i] != 0){
lib.erase(del[i]);
}
tmp = lib.size();
ans = max(tmp , ans);
}
cout << ans << endl;
return 0;
}C - Geometric Progression
枚举每个元素a[i]。将其当做等比数列的第二项,假设a[i]/k 与 a[i]*k存在。则将a[i]/k 与 a[i]*k的数量相乘并累加。
英文题解好像解释的更清楚些。。
Let's solve this problem for fixed middle element of progression. This means that if we fix element
ai then the progression must consist of
ai / k and
ai·k elements. It could not be possible, for example, if
ai is not divisible by
k (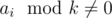 ).
).
For fixed middle element one could find the number of sequences by counting how many ai / k elements are placed left from fixed element and how many ai·k are placed right from it, and then multiplying this numbers. To do this, one could use two associative arrays Al and Ar, where for each key x will be stored count of occurences of x placed left (or right respectively) from current element. This could be done with map structure.
Sum of values calculated as described above will give the answer to the problem.
/*
* @author Novicer
* language : C++/C
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
#include<iomanip>
#define INF 2147483647
#define cls(x) memset(x,0,sizeof(x))
#define rise(i,a,b) for(int i = a ; i <= b ; i++)
using namespace std;
const double eps(1e-8);
typedef long long lint;
const int maxn = 2 * 100000 + 5;
lint a[maxn];
map<lint , lint> l;
map<lint , lint> r;
int main(){
// freopen("input.txt","r",stdin);
int n;
lint k;
cin >> n >> k;
for(int i = 1 ; i<= n ; i++){
scanf("%I64d",&a[i]);
r[a[i]]++;
}
lint ans = 0;
for(int i = 1 ; i <= n ; i++){
r[a[i]]--;
if(a[i] % k == 0)
ans += l[a[i]/k] * r[a[i]*k];
l[a[i]]++;
}
cout << ans << endl;
return 0;
}D - One-Dimensional Battle Ships
非常有意思的一道题,长度为n的空间放着k条长度为a的船,且船不重叠,Alice给你m个宣称miss(即没有船)的位置。推断Alice是否撒谎,若撒谎输出第一次能够发现矛盾的位置。
思路:
题解思路太棒!
简单来说就是推断Alice说的位置将空间分为两个部分,计算出这两个部分各能容纳几艘船,加起来与k比較,大于则撒谎。
/*
* @author Novicer
* language : C++/C
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
#include<iomanip>
#define INF 2147483647
#define cls(x) memset(x,0,sizeof(x))
#define rise(i,a,b) for(int i = a ; i <= b ; i++)
using namespace std;
const double eps(1e-8);
typedef long long lint;
map<int , int> ship;
int n,k,a;
int f(int x){return (x+1)/(a+1);};//计算长度为x区间能容纳几艘船
int main(){
// freopen("input.txt","r",stdin);
while(cin >> n >> k >> a){
ship.clear();
int m ; cin >> m;
ship[0] = ship[n+1] = 1;
int max_sum = f(n);
bool cheat = false;
for(int i = 1 ; i <= m ; i++){
int shot;
scanf("%d",&shot);
if(ship.find(shot) != ship.end()) continue;
ship[shot] = 1;
int l , r;
map<int , int>:: iterator low = ship.lower_bound(shot);
map<int , int>:: iterator up = ship.upper_bound(shot);//low-1与up各自是最靠近shot的左右位置
l = (--low)->first;
r = up->first;
max_sum -= f(r - l - 1);
max_sum += f(r - shot - 1) + f(shot - l - 1);
if(max_sum < k){
cheat = true;
cout << i << endl;
return 0;
}
}
if(!cheat)
cout << -1 << endl;
}
return 0;
}




For problem D, simply use a map structure to record the free space (a consecutive empty square without shotpoint) on a shotpoint's left and right.
You can use the lower_bound and upper_bound functions to find the nearest shotpoint, and update them.
When a shot happens a free space will be broken into 2, so calculate the sum of max number of ships of those 2 spaces and subtract it from the global sum of max number of ships.
Calculate the maximum number of ships could be placed in the space: (space+1)/(a+1)
(global sum of max number of ships = (n+1)/(a+1) before the 1st shot.)
when the global sum < k just print the current operation number and exit.