二、数学建模之误差分析和模型检验

1、介绍

• 建模前的数据的预处理
• 建立模型后的分析和检验

2、误差分析

2.1 理论分析

该原理来自于高等数学：

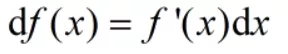
此公式具有普遍性，但有也例外：

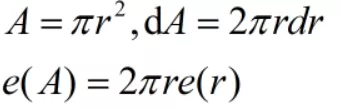
• 一元函数误差分析
  
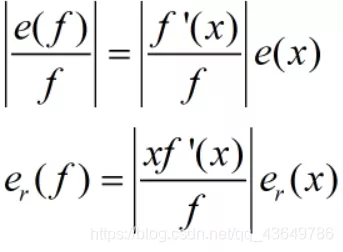
  为保证可比性，通常将绝对误差转换经过变形加绝对值转换为相对误差。

绝对误差：|测量值-真实值|
相对误差：|测量值-真实值|/真实值

• 二元函数误差分析——利用全微分理论知识
  
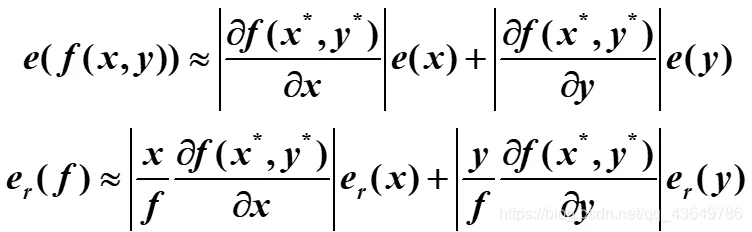
  对于得到的结果而言因变量的系数越大，就越能够认为该因子（自变量）是模型的中重要影响因子，即敏感因子。

2.2扰动分析

对重要参数进行扰动（人为），观察计算结果的变化。例如：直接让重要参数增加或减少1%，计算得到的结果发生的变化

3、稳定性分析

3.1 微分方程、差分方程稳定性理论分析

• 方程解是否在可控范围内稳定
• 解对微分方程系数的依赖程度

3.2 扰动分析

4、模型检验

4.1 实际实验检验

在理论之外直接动手进行操作。例如：直接到场地进行检验，通过带入数据对模型进行测量，求解结果对在实际试验所得到的结果进行对比分析。确定模型的准确性

4.2 扰动分析

5、敏感性分析

5.1 线性规划问题Lingo求解：直接给出

5.2 扰动分析

将模型中的参数以控制变量法进行调试，通过保持其他变量不变而对某一单独变量进行范围扰动，观察结果的变化程度，变换程度极大的则可以认为该变量所对应的影响因子敏感性较大，对于模型具有重要的影响关系，最后通过对比常识或相关研究资料验证是否合理