一、数学建模之马尔可夫预测方法

有关事件发生的概率预测：对事件的全面预测，不仅要指出事件发生的各种可能结果，还要指出每种可能结果发生的概率。

Markov方法：就是一种关于事件发生的概率预测的方法。是一种根据目前状态预测将来各个时刻或者时期的变动状态的预测方法。例如：天气预报

1、状态、状态转移过程和Markov过程

1.1 状态

是一种“术语”，是指某一个事件在某一时刻出现的可能结果（某一事件在某一刻出现的该类），比如说：商品在某一刻“畅销”，在某一刻“冷淡”，下雨在某一个时刻“大雨”、“中雨”，这就是事件发生的一种状态。

1.2 状态转移过程

• 状态转移：在事件的不断发展中，这一可能结果会从一个状态向另一个状态转移，被称为状态转移。例如：从“大雨”到“小雨”的状态就是一种状态转移
• 状态转移过程：状态转移与时间的关系，被称为状态转移过程，用数学表示就是y=f（t），y:是状态变量，t是时间变量。或者说事件发展随着时间的变化而变化所作的状态转移被称为状态转移过程。

1.3 状态转移概率和状态转移概率矩阵

• 状态转移概率：在事件的发展过程中，从一个状态出发，下一刻转移到另一个状态的可能性被称为状态转移概率（从一个状态转移到另一个状态的可能性）。
• 状态转移概率矩阵：某一被预测事件有E1、E2、E3、...、En中状态，Pij为从状态Ei转移到状态Ej的概率，则有矩阵：
  
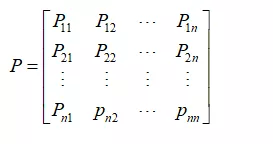
  （就是一种所有状态转移概率的表示方法）称矩阵P为状态转移矩阵。
  
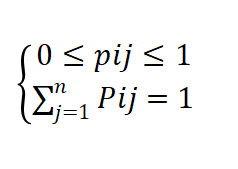
  满足上方条件的任何矩阵称为随机矩阵，或者概论矩阵。
• 标准概率矩阵：P为概率矩阵，存在m>0，使得矩阵Pm中诸元素皆非零，称P为标准概率矩阵。

1.4 状态转移概率矩阵的计算

• 计算状态转移概率矩阵就是计算每个状态转移到其他任何一个状态的转移概率。可以采用频率近似概率的方法，不过要求就是数据足够大
  例如：从状态E1->E1,E1->E2,E1->E3。
  

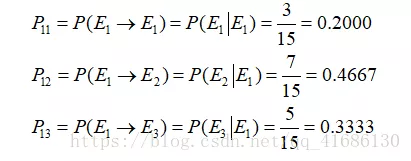
1.5 Markov预测法

• 状态概率：为了马尔可夫概率预测方法对事件发展过程中状态出现的概率进行预测，介绍状态概率Πj(k)的概念，Πj(k)表示：初始时状态（k=0）为已知条件下，经过k次状态转移过程（含有时间的定义）后，第K时刻处于状态Πj的概率。（解释：k表示事件，Πj表示k时刻后的状态，Πj(0)表示到状态Πj的初试状态）

由马尔可夫的无后效性和Bayes公式可得：

若记行向量π(k)=[π1(k)，π2(k)，…，πn(k)]，则由上式可得逐次计算状态概率的递推公式：

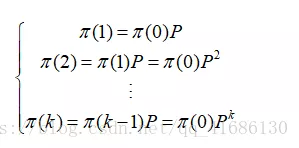
π（0)=[π1（0)，π2（0)，…，πn（0)]为初始状态概率向量

• 分析：如果某一事件在第0个时刻（或时期)的初始状态已知（即π（0)已知)，则利用递推公式，就可以求得它经过k次状态转移后，在第k个时刻（时期)处于各种可能的状态的概率（即π（k))，从而得到该事件在第k个时刻（时期)的状态概率预测。