数据结构与算法基础之图的应用

第一节数据结构与算法基础之图的应用-最小生成树

一、回顾

生成树

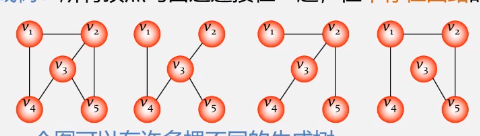
  1. 所有顶点均由边连接，且不连接

  2. 所有生成树具有以下不同热点:

    • 生成树的顶点个数与图的顶点个数相同
    • 生成树是图的极小连通子图，去掉一条边则非连通
    • 生成树任意两点间的路径是唯一的
    • 一个有n个顶点的连通图的生成树有n-1条边
    • 生成树中再加一条边必形成回路

  3. 含有n个顶点n-1条边的图不一定是生成树

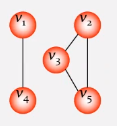
无向图的生成树

利用图的深度优先遍历生成-->深度优先生成树

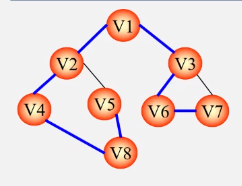
利用图的广度优先遍历生成-->广度优先生成树

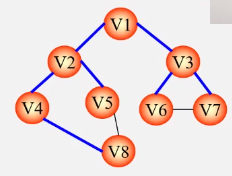
构造生成树思路：顶 点用边连起来，还不能出现回路。

构造生成树原则：

  • 必须只是用该网中的边来构造
  • 必须使用且仅使用n-1条边连结网络总的n个顶点
  • 不能产生回路的边

二、最小生成树

定义：给定一个无向网络，该网的所有生成树中，使各边权值之和最小的那棵生成树称该网的最小生成树，也叫最小代价生成树

求最小生成树

  • 使用不能遍历图的方法，可以得到不同的生成树
  • 从不同顶点出发，可以得到不同的生成树
  • MST性质（Minimum Spanning Tree）
    • 设N = （V,E）是一个联通网，U是顶点集V的一个非空子集。若边（u，v）是一条具有最小权值的边，其中u∈U，v∈V-U，则必存在一棵包含边（u，v）的最小生成树
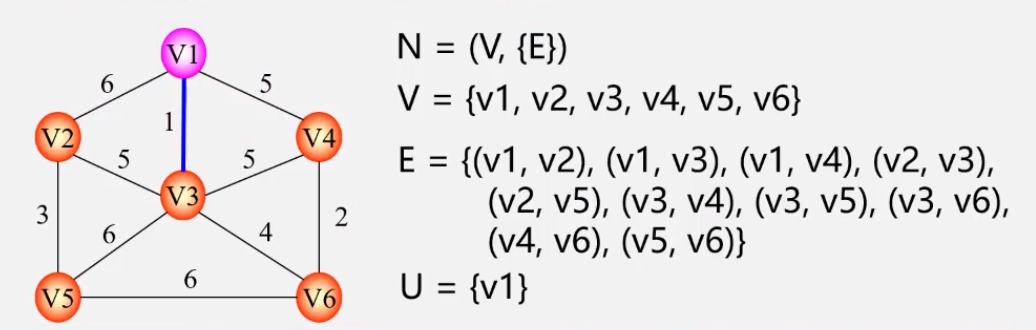
    • MST性质解释
      • 生成树构造过程中，图中n个顶点属于两个集合：
        1. 已落在生成树上的顶点集:U
        2. 尚未落在生成树上的顶点集:V-U
      • 在所有连通U中顶点和V-U中顶点的边中选权值最小的边

构造最小生成树方法一：普力姆算法（Prim）

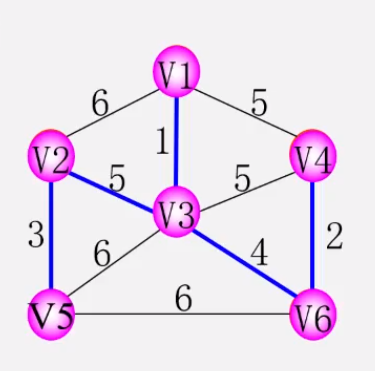
算法思想：

* 设N = （V,E）一个连通网，TE是N上最小生成树的**边的集合**         解释：有一个连通网，TE是最小生成树
* 初始化令U={uo}，（uo∈V，）TE={}                               解释：初始化：TE没有边，U也没有最小生成树的顶点集合
* 在所有u∈U，v∈V-U的边（u，v）∈E中，找一条代价最小的边（uo，vo） 解释：在所有顶点中随意找一个顶点，此顶点属于并入最小生成树的顶点。然后在与非并入TE的顶点中找一条**代价最小的边**
* 将（uo，vo）并入集合TE，同时vo并于U                             解释：将代价最小边并入最小生成树
* 重复上述操作，直到U=V为止，则T=(V,TE)为N的最小生成树             解释：在并入最小生成树中的顶点中，找连接非并入最小生成树顶点的代价最小边，然后重复
  • 第一步：
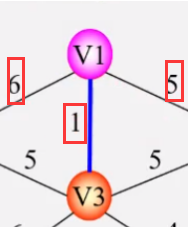
  • 第二步：
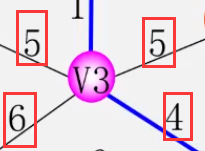
  • 第三步：
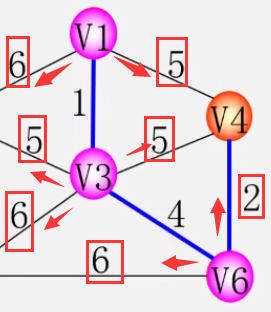
  • 第四步：
  • 第五步：

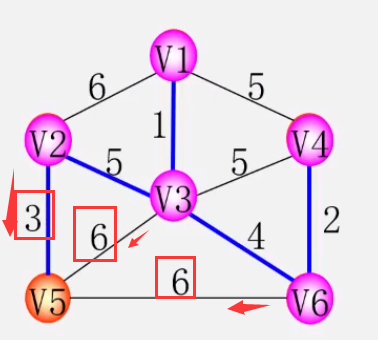
构造最小生成树方法一：克鲁斯卡尔算法（Kruskal）

算法思想：

* 设N = （V,E）一个连通网，令最小生成树初始状态为**只有n个顶点而无边**的非连通图T=（V,{}）,每个顶点自成一个连通分量。
* 在E中选取代价最小的边，该边依附的顶点落在T中不同连通分量上**（不能成为环）**，则将此边加入T中，否则，舍去此边。
* 依次类推，直至T中所有顶顶啊都在同一连通分量上为止。
  • 第一步：
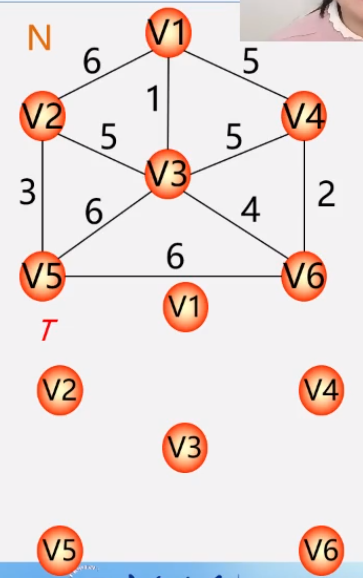
  • 第二步：
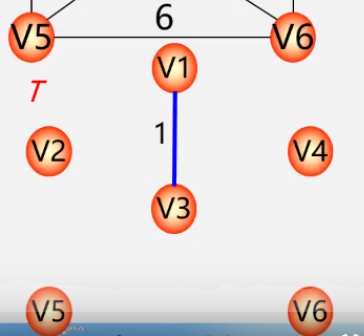
  • 第三步：
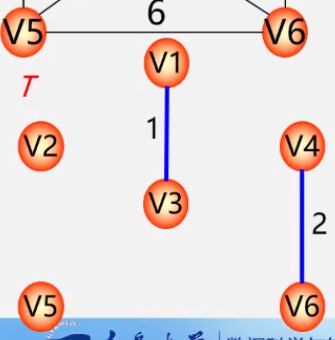
  • 第四步：
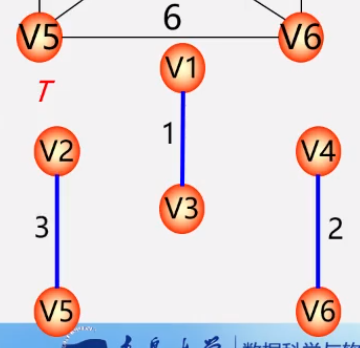
  • 第五步：
  • 第六步：

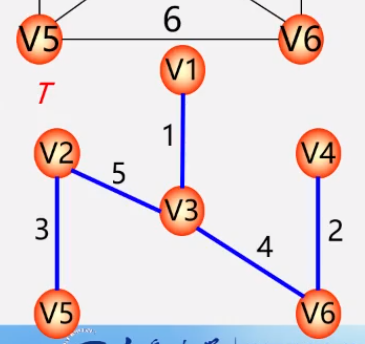
注意：最小生成树可能不唯一

两种算法比较：

算法名 普里姆算法（Prim） 克鲁斯卡尔算法(Kruskal)
算法思想 选择点 选择边
时间复杂度 O（n²）（n为顶点数） O（eloge）（e为边数）
适应范围 稠密图 稀疏图

第二节数据结构与算法基础之图的应用-最短路径

1.应用举例

　　交通网络问题——从甲地到乙地之间是否有公路连通？在有多条通路的情况下，哪一条路最短？

　　交通网络用有向图来表现：

　　顶点—>表示地点

　　弧——>表示两个有路连通，

　　弧上的权值—>表示两地点之间的距离、交通费或途中所花费的时间

2.最短路径：

  • 在有向网中A点 到 B点的多条路径中，寻找一条各边权值之和最小的路径，即最短路径
  • 即各边权值之和最小

最小生成树与最短路径的不同：路径上不一定包含n个顶点，也不一定包含n-1条边

3.最短路径遇到的问题

3.1第一类问题：两点间最短路径
*已知任意源点和终点，求最短路径

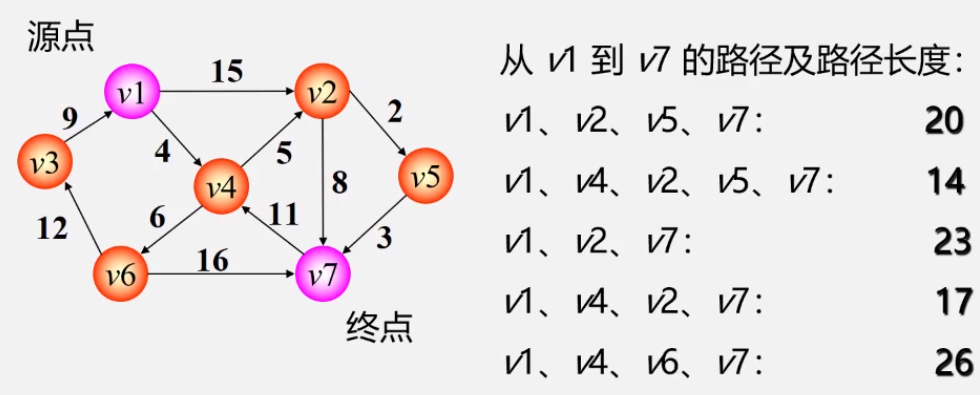
image

3.2第二类问题：某源点到其他各点最短路径

image

4.两种常见的最短路径问题

  • 单源最短路径——用Dijkstra（迪杰斯特拉）算法
  • 所有顶点间的最短路径——用Floyd（弗洛伊德）算法

4.1Dijistra算法：按路径长度递增次序产生最短路径

  1. 初始化：先找出从源点Vo到各终点Vk的直达路径（Vo，Vk）——>通过一条弧到达的路径
  2. 选择：从这些路径中找出一条长度最短的路径（Vo，u）
  3. 更新：然后对其余各条路径进行适当调整：
    * 若图中存在弧（u，Vk），且（Vo，u）+（u，Vk）<（Vo，Vk），则以路径（Vo，u，Vk）代替（Vo，Vk）

思路分析：

  • 将V（顶点集）分成两组：
    • S：已求出最短路径的顶点的集合
    • T=ｖ－Ｓ：尚未确定最短路径的顶点集合
  • 将T中顶点按最短路径递增的次序加入到S中。保证：
    • 从源点Vｏ到S中各顶点的最短路径长度都不大于从Vｏ到T中任何顶点的最短路径长度。
    • 每个顶点对应一个距离值：
      S中顶点：从Vo到此顶点的最短路径长度
      T中顶点：从Vo到此顶顶的只包括S中顶点中间顶点的最短路径长度

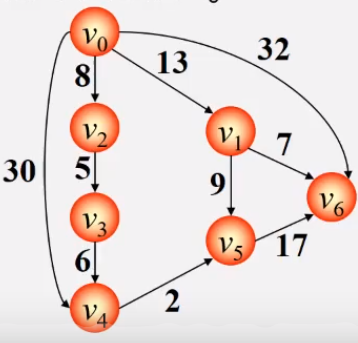
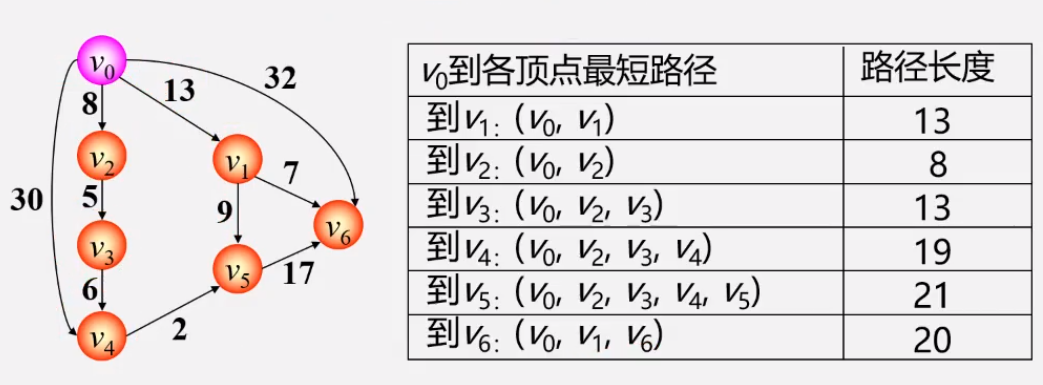
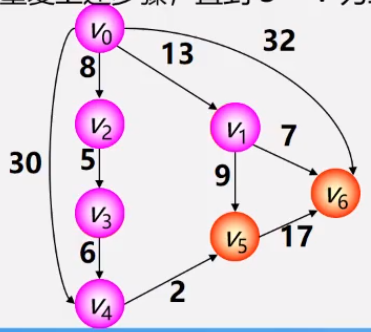
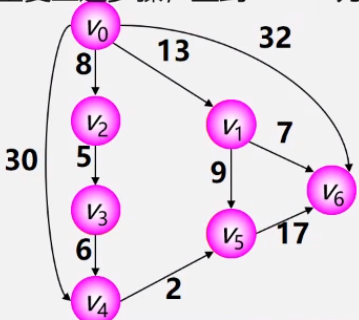
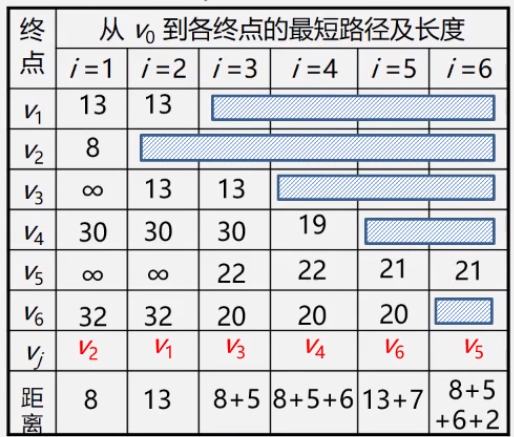
例题分析

  • 初始化时:S={Vo},T={其余顶点}。 T中顶点对应的权值用辅助数组D存放（D[i]）。
  • 第一步：从T中选取一个最小权值Vj加入S

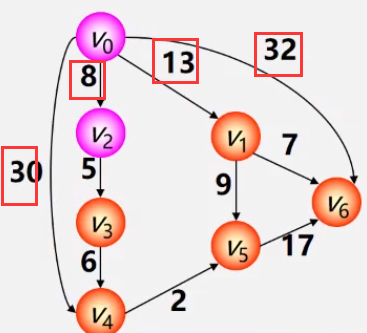
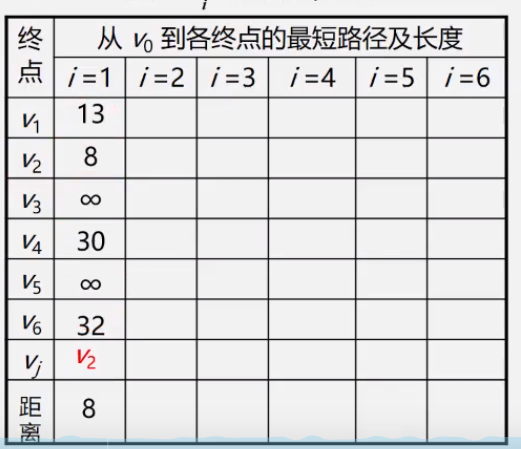
  • 第二步：对T中顶点距离进行修改（动态更新），以加入Vj作中间顶点，从Vo到Vi的距离值比 不加Vj的路径要短，则修改距离值

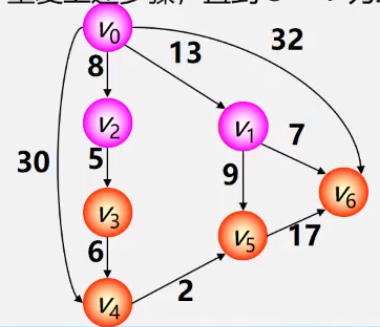
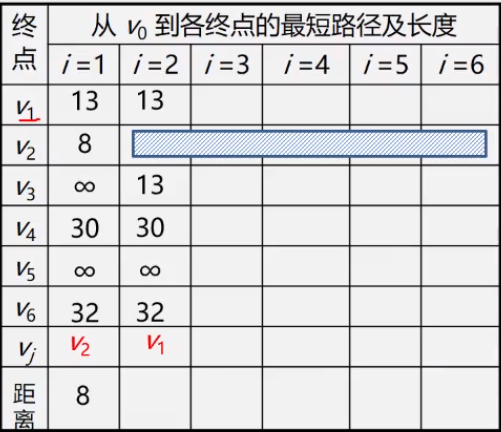
  • 第三步：

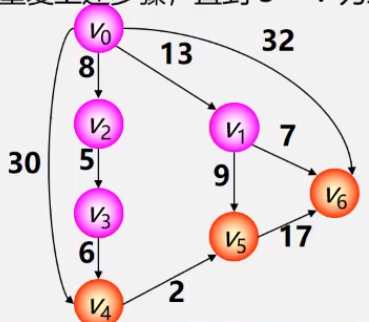
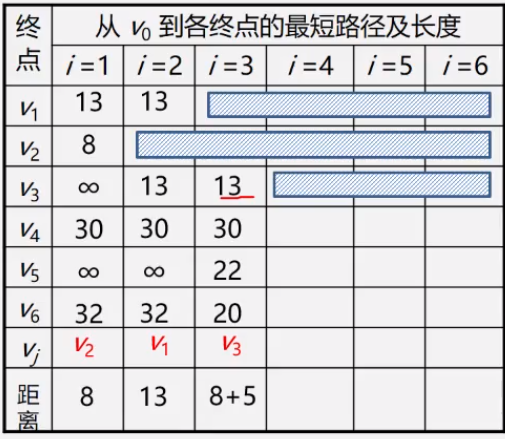
  • 第四步：

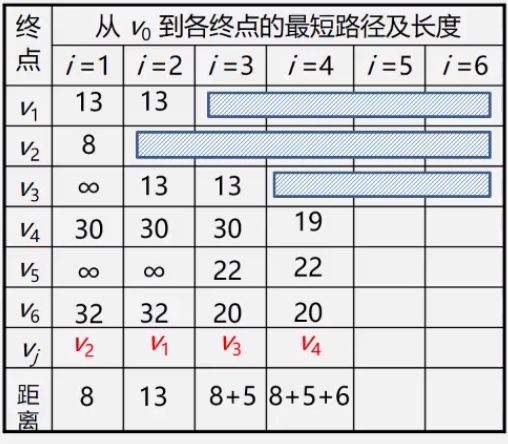
  • 第五步：

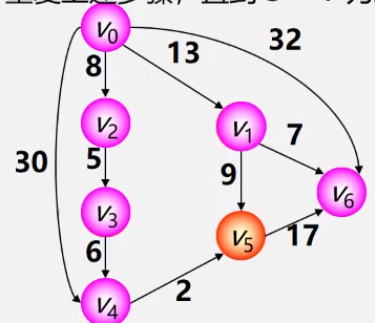
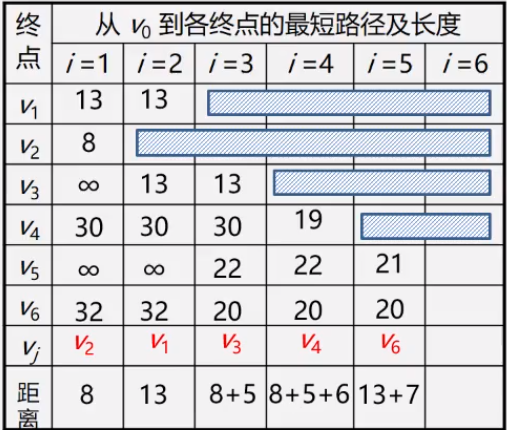
  • 第六步：

4.2Floyd算法：求图中各顶点之间的最短路径

算法思想：
* 逐个顶点试探
* 从Vi到Vj的所有可能存在的路径中
* 选出一条长度最短的路径
例题分析：

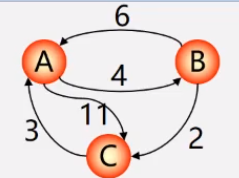
求解步骤
1. 初始化设置一个n阶方阵，令其对角线元素为0，若存在弧<Vi,Vj>,则对应元素为权值，否则∞

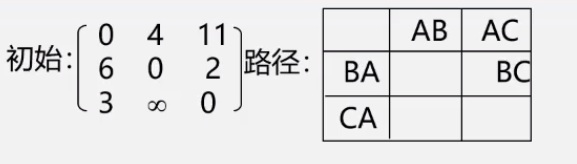
2. 逐步在原直接路径中增加中间顶点，若加入后路径变短，则修改。

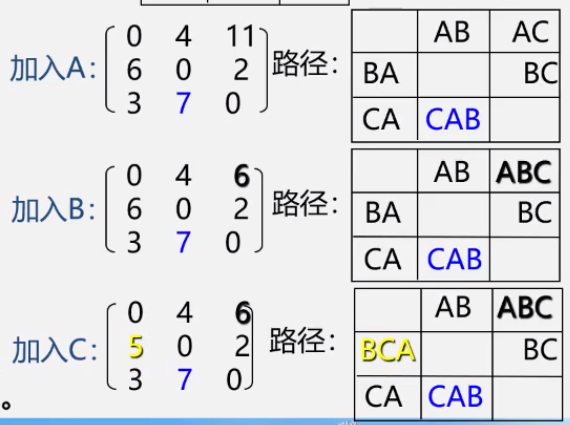
3. 最后的权值

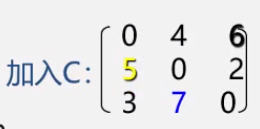
最后的路径：

第三节拓扑排序

posted @ 2021-05-23 11:13  登云上人间  阅读(23)  评论(0)  编辑  收藏  举报