分块莫队

莫队

序言

其实我不是很赞成把分块和莫队放到一起的（可能是我太菜了），原本这周先学的树上合并，树分治扫描线那些的，但是没怎么懂，先写一个记忆最新的吧。

简介

莫队算法是由莫涛提出的算法，莫队算法可以解决一类离线区间询问问题，适用性极为广泛。同时将其加以扩展，便能轻松处理树上路径询问以及支持修改操作。

其实就是暴力，不过是更加优美的暴力。

咳咳，不过其实莫队的实现因为很容易，相较于市面上的那些码量动不动上百行的算法，可以说是很仁慈了，而且很容易入手（当然个例分支除外）。

普通莫队

现在我们考虑这么一个问题：

给定一个序列，我们每次询问一个区间，询问这个区间里的不同元素的个数。

现在肯定又有人要跳出来说用线段树了，那你请出门左转 luogu 去看看 noip 出的（毒瘤）题单，这时候你会发现 ~~线段树就是弱智才去写的~~。

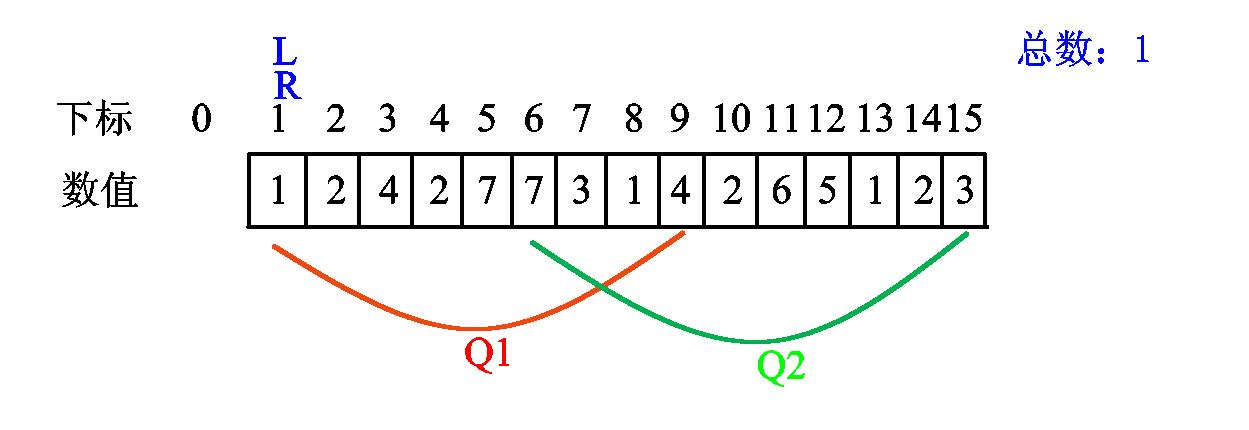
莫队的思想就是我们定义两个指针 \(l\)，\(r\) 表示莫队的区间，然后我们将所有询问区间离线下来离散化，按照左端点排序，然后每次优先把 \(l\)，向最近的询问区间移动，然后移动 \(r\) 就行。

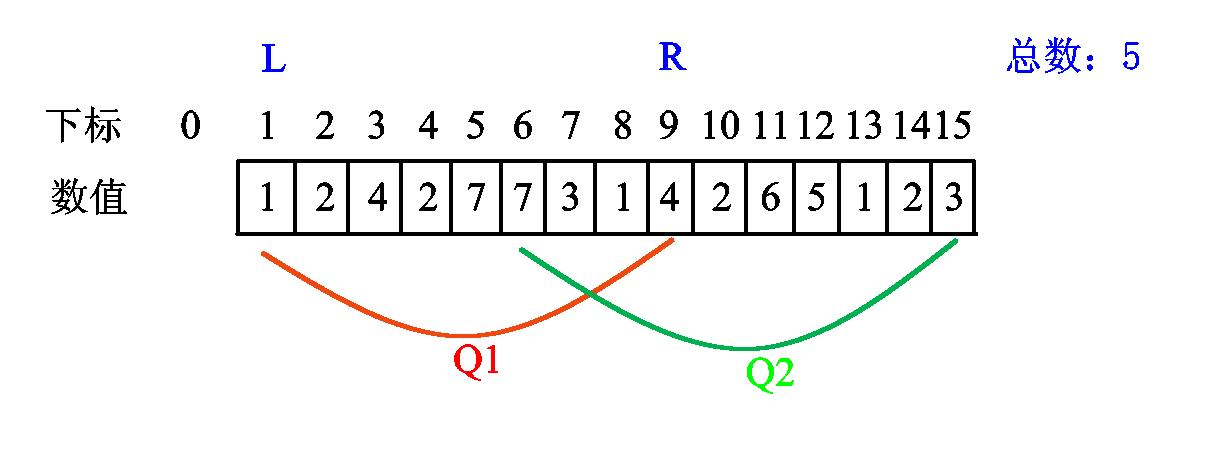
给个示意图吧：

我们初始化 \(l=1,r=0\)，下面开始移动两个指针。

我们发现 \(l\) 已经是查询区间的左端点了，现在开始移动 \(r\) 到 \(Q_1\) 的右端点，右移一位，发现新数值 1，总数 +1 。

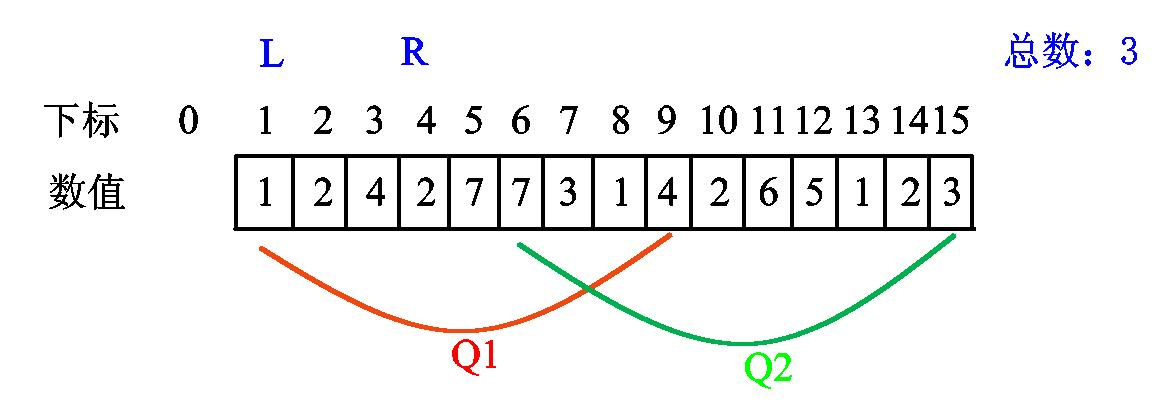
接着移动，遇到 2 答案 +1。

直到遇到第二个 2，总数不变（这个可以用个 map 啥的记录一下出现过的）。

接下来两个 7 同理，总数+1。

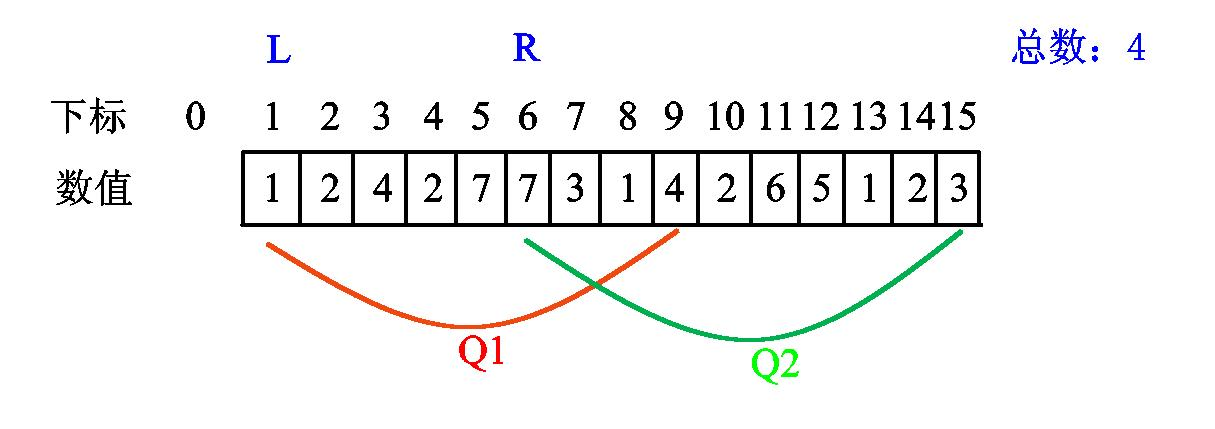
继续

最后两个都访问过了，总数不加。

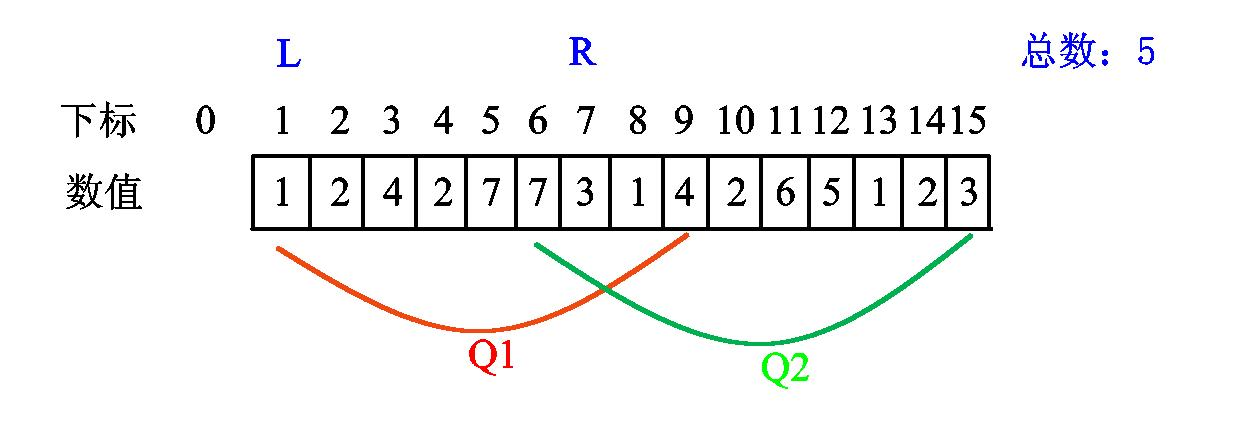
至此，我们处理完了第一个询问的区间答案，答案为 5。

下面处理 \(Q_2\) 的问题，需要先把 \(l\) 移动到其左区间，剩下的操作和之前一样。

注意 \(l\) 右移时，需要判断一下当前元素删掉会不会使得总数减少，这个同理也是用 map 记录下来过的。

粘个我认为写的很好的代码吧：

int aa[maxn], cnt[maxn], l = 1, r = 0, now = 0; //每个位置的数值、每个数值的计数器、左指针、右指针、当前统计结果（总数）
void add(int pos) {//添加一个数
    if(!cnt[aa[pos]]) ++now;//在区间中新出现，总数要+1
    ++cnt[aa[pos]];
}
void del(int pos) {//删除一个数
    --cnt[aa[pos]];
    if(!cnt[aa[pos]]) --now;//在区间中不再出现，总数要-1
}
void work() {//优化2主过程
    for(int i = 1; i <= q; ++i) {//对于每次询问
        int ql, qr;
        scanf("%d%d", &ql, &qr);//输入询问的区间
        while(l < ql) del(l++);//如左指针在查询区间左方，左指针向右移直到与查询区间左端点重合
        while(l > ql) add(--l);//如左指针在查询区间左端点右方，左指针左移
        while(r < qr) add(++r);//右指针在查询区间右端点左方，右指针右移
        while(r > qr) del(r--);//否则左移
        printf("%d\n", now);//输出统计结果
    }
}

但其实这个代码的思路其实是不完整的，我们考虑这样的一个情况：

这样的话，\(l\) 和 \(r\) 就会左跳一下右跳一下，直接寄。

接下来就是优化了。

优化1

分块大法好！我们把序列分成 \(\sqrt{n}\) 个块，然后将询问区间排序，按左端点从小到大排序，如果左端点在同一个块内，则按照右端点从小到大排序。这样复杂度就降到了 \(O(n\sqrt{n})\)。

下面乱胡一个证明（网上看的）:

排序复杂度 \(O(n\log n)\)。
左指针位移，假设最坏情况下每个询问都不在同一个块中，那么一次移动均摊最多是 \(O(\sqrt n)\) 的，所以总时间复杂度是 \(O(n\sqrt n)\)。
右指针位移，同理，最坏情况下每次移动会扫完整个序列，即 \(O(n)\)，但是总共只有 \(\sqrt n\) 个块，意味着最多只会有 \(\sqrt n\) 个不在一个块的左端点，所以右指针移动的次数最多是 \(O(\sqrt n)\)，所以总时间复杂度是 \(O(n\sqrt n)\)。

综述，莫队的复杂度为 \(O(n\log n)+O(n\sqrt n)+O(n\sqrt n)=O(n\sqrt n)\)。

参考的排序 cmp 函数

int cmp(query a, query b) {
    return belong[a.l] == belong[b.l] ? a.r < b.r : belong[a.l] < belong[b.l];
}

优化玄学卡常

1. #pragma GCC optimize(2) and #pragma GCC optimize(3)

不好多说了，反正吸个氧的莫队速度飞快，\(1e6\) 毫无压力。

2. 奇偶性排序

网上学的，看起来没什么鸟用，其实会让代码平均每个点快 \(200ms\) 左右。

思路就是对于左端点在同一奇数块的区间，右端点按升序排列，反之降序。

主要原理便是右指针跳完奇数块往回跳时在同一个方向能顺路把偶数块跳完，然后跳完这个偶数块又能顺带把下一个奇数块跳完。理论上主算法运行时间减半，实际情况有所偏差。（不过能优化得很爽就对了）

代码：

int cmp(query a, query b) {
	return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}

3.函数拆分

就是把 \(add\) 和 \(del\) 硬生生拆开，速度更快（我不李姐）。

while(l < ql) now -= !--cnt[aa[l++]];
while(l > ql) now += !cnt[aa[--l]]++;
while(r < qr) now += !cnt[aa[++r]]++;
while(r > qr) now -= !--cnt[aa[r--]];

现在代码也就不难写了

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;

#define maxn 1010000
#define maxb 1010
int aa[maxn], cnt[maxn], belong[maxn];
int n, m, size, bnum, now, ans[maxn];
struct query {
	int l, r, id;
} q[maxn];

int cmp(query a, query b) {
	return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
#define isdigit(x) ((x) >= '0' && (x) <= '9')
int read() {
	int res = 0;
	char c = getchar();
	while(!isdigit(c)) c = getchar();
	while(isdigit(c)) res = (res << 1) + (res << 3) + c - 48, c = getchar();
	return res;
}
void printi(int x) {
	if(x / 10) printi(x / 10);
	putchar(x % 10 + '0');
}

int main() {
	scanf("%d", &n);
	size = sqrt(n);
	bnum = ceil((double)n / size);
	for(int i = 1; i <= bnum; ++i) 
		for(int j = (i - 1) * size + 1; j <= i * size; ++j) {
			belong[j] = i;
		}
	for(int i = 1; i <= n; ++i) aa[i] = read(); 
	m = read();
	for(int i = 1; i <= m; ++i) {
		q[i].l = read(), q[i].r = read();
		q[i].id = i;
	}
	sort(q + 1, q + m + 1, cmp);
	int l = 1, r = 0;
	for(int i = 1; i <= m; ++i) {
		int ql = q[i].l, qr = q[i].r;
		while(l < ql) now -= !--cnt[aa[l++]];
		while(l > ql) now += !cnt[aa[--l]]++;
		while(r < qr) now += !cnt[aa[++r]]++;
		while(r > qr) now -= !--cnt[aa[r--]];
		ans[q[i].id] = now;
	}
	for(int i = 1; i <= m; ++i) printi(ans[i]), putchar('\n');
	return 0;
}

带修莫队

带修莫队就是在普通莫队的基础上增加了修改操作。

例：P1903 [国家集训队] 数颜色 / 维护队列

题目描述

墨墨购买了一套 \(N\) 支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。墨墨会向你发布如下指令：

\(Q\ L\ R\) 代表询问你从第 \(L\) 支画笔到第 \(R\) 支画笔中共有几种不同颜色的画笔。
\(R\ P\ C\) 把第 \(P\) 支画笔替换为颜色 \(C\)。

为了满足墨墨的要求，你知道你需要干什么了吗？

输入格式

第 \(1\) 行两个整数 \(N\)，\(M\)，分别代表初始画笔的数量以及墨墨会做的事情的个数。

第 \(2\) 行 \(N\) 个整数，分别代表初始画笔排中第 \(i\) 支画笔的颜色。

第 \(3\) 行到第 \(2+M\) 行，每行分别代表墨墨会做的一件事情，格式见题干部分。

输出格式

对于每一个 Query 的询问，你需要在对应的行中给出一个数字，代表第 \(L\) 支画笔到第 \(R\) 支画笔中共有几种不同颜色的画笔。

样例 #1

样例输入 #1

6 5
1 2 3 4 5 5
Q 1 4
Q 2 6
R 1 2
Q 1 4
Q 2 6

样例输出 #1

修改操作也分两种，一种是离线可做，一种是强制在线，如果是强制在线基本上莫队就萎了，可离线的话还可以做，这道题就是属于离线可做的类型。做法就是对每个询问区间再加上一维时间维度 \(t\)。

做法是把修改操作编号，称为"时间戳"，而查询操作的时间戳沿用之前最近的修改操作的时间戳。跑主算法时定义当前时间戳为 \(t\) ，对于每个查询操作，如果当前时间戳相对太大了，说明已进行的修改操作比要求的多，就把之前改的改回来，反之往后改。只有当当前区间和查询区间左右端点、时间戳均重合时，才认定区间完全重合，此时的答案才是本次查询的最终答案。

通俗地讲，就是再弄一指针，在修改操作上跳来跳去，如果当前修改多了就改回来，改少了就改过去，直到次数恰当为止。

#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define PII pair<int,int>
#define mk(a,b) make_pair(a,b)
using namespace std;
template<typename P>
inline void read(P &x){
    P res=0,f=1;
    char ch=getchar();
    while(ch<'0' || ch>'9'){
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9'){
        res=res*10+ch-'0';
        ch=getchar();
    }
    x=res*f;
}
int T=1;

const int N=250000;
const int M=1111111;

int n,m;
int cnt[M],a[N],ans[N],sum,cntq=0,cntr=0,siz;
struct dat{
    int l,r,t,id;
}qq[N];
struct change{
    int pos,val;
}qr[N];

inline bool cmp(dat a,dat b){
	return a.l/siz==b.l/siz?a.r/siz==b.r/siz?a.t<b.t:a.r<b.r:a.l<b.l;
}

inline void add(int x){
    if(!cnt[x]) ++sum;
    cnt[x]++;
}
inline void del(int x){
    cnt[x]--;
    if(!cnt[x]) --sum;
}

inline void update(int x,int t){
    if(qq[x].l<=qr[t].pos && qr[t].pos<=qq[x].r){
        del(a[qr[t].pos]);
        add(qr[t].val);
    }
    swap(a[qr[t].pos],qr[t].val);
}

signed main(){
	read(n),read(m);
	siz=pow(n,0.666);
	for(int i=1;i<=n;++i) read(a[i]);
	for(int i=1;i<=m;++i){
		char opt;
		int l,r;
		cin>>opt;
		read(l),read(r);
		if(opt=='Q') qq[++cntq].l=l,qq[cntq].r=r,qq[cntq].t=cntr,qq[cntq].id=cntq;
		else qr[++cntr].pos=l,qr[cntr].val=r;
	}
	sort(qq+1,qq+cntq+1,cmp);
	int l=1,r=0,t=0;
	for(int i=1;i<=cntq;++i){
		while(l<qq[i].l) del(a[l++]);
		while(l>qq[i].l) add(a[--l]);
		while(r>qq[i].r) del(a[r--]);
		while(r<qq[i].r) add(a[++r]);
		while(t<qq[i].t) update(i,++t);
		while(t>qq[i].t) update(i,t--);
		ans[qq[i].id]=sum;
	}
	for(int i=1;i<=cntq;++i) printf("%d\n",ans[i]);
    return 0;
}

剩下的莫队不会，以后再学吧。

posted @ 2024-08-28 14:54 God_Max_Me 阅读(7) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

God_Max_Me的小站