【数据结构&算法】13-赫夫曼树&赫夫曼编码
前言
参考：
李柱明博客：https://www.cnblogs.com/lizhuming/p/15487422.html
概念
路径：在一棵树中，一个结点到另一个结点之间的通路，称为路径。
路径长度： 路径上的分支数目称为路径长度。
树的路径长度：从树根到每个结点的路径长度。
结点的权：给每一个结点赋予一个新的数值，被称为这个结点的权。
- 如，下图中结点 a 的权为 7，结点 b 的权为 5。
结点的带权路径长度：指的是从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度：树中所有叶子结点的带权路径长度之和。通常记作 WPL。
赫夫曼树（Huffman）：带权路径长度 WPL 最小的二叉树称做赫夫曼树。也叫最优二叉树。
- 注：哈夫曼树中没有度为 1 的结点。
想法：
-
为什么数据只能是叶子结点？
- 参考赫夫曼编码来理解。只使用叶子结点就避免了每个数据中可能存在其前缀路径是一个数据的问题。因为每个数据都是叶子，所以数据路径前面、后面都没数据结点。具体去看一下赫夫曼编码过程即可。
构造最优赫夫曼树
图表实现
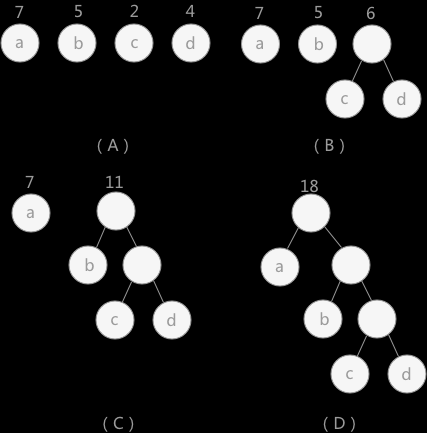
给定的有各自权值的 n 个结点，构造最优赫夫曼树步骤：
-
在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和。
- 两个结点中权值较小的为左孩子。
-
在原有的 n 个权值中删除那两个最小的权值，同时将新的权值加入到 n–2 个权值的行列中。
-
重复 1、2 步骤。
赫夫曼树中的结点结构
基本数据：
-
权重
-
父节点
- 由于赫夫曼树的构建是从叶子结点开始，不断地构建新的父结点，直至树根，所以结点中应包含指向父结点的指针。
-
左孩子
-
右孩子
参考代码：
//哈夫曼树结点结构
typedef struct {
int weight; // 结点权重
int parent; // 父结点
int left; // 左孩子
int right; //右孩子
}ht_node_t, *huffman_tree_p;
赫夫曼树算法实现
构建哈夫曼树时，需要每次根据各个结点的权重值，筛选出其中值最小的两个结点，然后构建二叉树。
思想：遍历无父结点。找出两个最小的无父结点。
- 无父结点说明该结点还未被建成树。
实现代码部分：
-
遍历找出两个最小的无父结点：
- 遍历找出第一个无父结点。
- 找出第二个无父结点，并与第一个进行比较，然后按大小存放到相应位置。
- 使用上面两个无父结点与后续的无父结点进行比较。
-
构建赫夫曼树：
-
申请内存，大小需要了解二叉树的性质三。
- 二叉树性质三：n0 = n2+1。由于赫夫曼树没有度为 1 的结点，所以知道叶子结点也就知道了该树的总结点数。
- 内存空间使用分配：前面是叶子结点，后面是辅助的组合新结点。参考下面内存图片。
-
初始化内存。先全清空，再把叶子结点的权重写入。
-
构建赫夫曼树：
- 遍历有权重的树组（即是内存前面部分），找出两个最小的无父结点。
- 把这两个结点组合出一个新的父结点，使用新的空结点内存保存。
- 循环上面 2.3.1 和 2.3.2 步骤，直至使用了最后一个结点空间。
-
申请的内存块在函数中的使用过程如下图：
- 叶子结点内存：是固定的，是数据。
- 已使用的新结点内存：是构建赫夫曼树时需要的辅助空结点。
- 未使用的新结点内存：供给创建赫夫曼树时辅助使用。
赫夫曼编码
赫夫曼树常见的应用就是赫夫曼编码了。
赫夫曼编码：
- 是在赫夫曼树的基础上构建的。
- 赫夫曼编码方式最大的优点就是用最少的字符包含最多的信息内容。
赫夫曼编码过程：（字符串为例）
- 根据字符串内容，统计出每个相同字符出现的次数，作为该字符的权值。把这些带权值的字符，建立赫夫曼树。
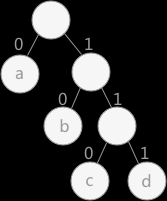
- 规定左孩子标记为 0，右孩子标记为 1。（也可以反过来，具体看需求）
- 然后从根节点开始遍历每个叶子结点，依次写出经过结点的标记，最终得到的就是该结点的哈夫曼编码。
如下图：
- a 的赫夫曼编码为：0
- b 的赫夫曼编码为：10
- c 的赫夫曼编码为：110
- d 的赫夫曼编码为：111
疑问：
- 问：编码长度不一样，不怕码表前面重复了出现误判吗？
- 答：不会。因为每个字符数据都在叶子结点，叶子结点路径前面没有数据，后面也没有数据。
参考代码
创建赫夫曼树
/** @file huffman_tree.c
* @brief 赫夫曼树
* @details 详细说明
* @author lzm
* @date 2021-10-18 21:16:12
* @version v1.0
* @copyright Copyright By lizhuming, All Rights Reserved
* @blog https://www.cnblogs.com/lizhuming/
*
**********************************************************
* @LOG 修改日志:
**********************************************************
*/
#include <string.h>
#include <stdlib.h>
#define HT_OK 0
#define HT_ERROR -1
//哈夫曼树结点结构
typedef struct {
int weight; // 结点权重
int parent; // 父结点
int left; // 左孩子
int right; //右孩子
}ht_node_t, *huffman_tree_p;
/**
* @name ht_select
* @brief 在传入的树组中检索出两个最小的权值结点，并把者两个结点从小到大放到index_mina
* @param
* @retval
* @author lzm
*/
int ht_select(huffman_tree_p ht, int index_end, int *index_mina, int *index_minb)
{
int i = 0;
int j = 0;
int weight_mina = 0;
int weight_minb = 0;
/* 1. 先找出第一个无父结点 */
while(ht[i].parent != 0)
{
i++;
if(i >= index_end)
return HT_ERROR;
}
weight_mina = ht[i].weight;
*index_mina = i;
/* 2. 寻找第二个无父结点 */
i++;
while(ht[i].parent != 0)
{
i++;
if(i > index_end)
return HT_ERROR;
}
if(ht[i].weight < weight_mina)
{
weight_minb = weight_mina;
*index_minb = *index_mina;
weight_mina = ht[i].weight;
*index_mina = i;
}
else
{
weight_minb = ht[i].weight;
*index_minb = i;
}
/* 遍历剩下数据，找出更小的 */
for(j = i+1; j <= index_end; j++)
{
if(ht[i].parent != 0)
continue;
if(ht[i].weight < weight_minb)
{
if(ht[i].weight < weight_mina)
{
weight_minb = weight_mina;
*index_minb = *index_mina;
weight_mina = ht[i].weight;
*index_mina = i;
}
else
{
weight_minb = ht[i].weight;
*index_minb = i;
}
}
}
return HT_OK;
}
/**
* @name ht_create_huffman_tree
* @brief 创建赫夫曼树
* @param ht:赫夫曼树地址。二级指针。
* @retval
* @author lzm
*/
int ht_create_huffman_tree(huffman_tree_p *ht_ptr, int *weight_a, int n)
{
int i = 0;
int num_ht = 2*n-1; // 二叉树性质3
huffman_tree_p ht = NULL;
if(n <= 1)
return HT_ERROR;
/* 申请内存 */
ht = (huffman_tree_p)malloc((num_ht+1) * sizeof(ht_node_t)); // 0 号位置保留，方便判断父结点域为空。
if(ht == NULL)
{
return HT_ERROR;
}
memset(ht, 0x00, (num_ht+1) * sizeof(ht_node_t));
/* 赋值叶子结点权值 */
for(i = 1; i <= n; i++)
{
ht[i].weight = weight_a[i-1];
}
/* 开始构建huffman tree */
for(i = n+1; i <= num_ht; i++)
{
int err = HT_OK;
int index_mina = 0;
int index_minb = 0;
err = ht_select(ht, i-1, &index_mina, &index_minb);
if(err != HT_OK)
{
free(ht);
return HT_ERROR;
}
ht[index_mina].parent = i;
ht[index_minb].parent = i;
ht[i].weight = ht[index_mina].weight + ht[index_minb].weight;
ht[i].left = index_mina;
ht[i].right = index_minb;
}
*ht_ptr = ht;
return HT_OK;
}
赫夫曼编码方法 1-逆序
typedef char **huffman_code_p;
/**
* @name ht_huffman_encode
* @brief 赫夫曼编码
* @param n:n个结点数
* @retval
* @author lzm
*/
int ht_huffman_encode(huffman_tree_p ht, huffman_code_p *hc_ptr, int n)
{
int i = 0;
char *hcc = NULL;
huffman_code_p hc = NULL;
hc = (huffman_code_p)malloc((n+1) * sizeof(char *)); // 该空间存放每个字符的编码值的地址（申请存放一级指针的空间赋值给二级指针）
if(hc == NULL)
return HT_ERROR;
hcc = (char *)malloc(n * sizeof(char)); // 该空间为一个字符的编码空间（本函数通用） 该空间存放每个字符的各个编码值（申请数据的空间赋值给一级指针）
if(hcc == NULL)
{
free(hc);
return HT_ERROR;
}
memset(hc, 0x00, (n+1) * sizeof(char *));
memset(hcc, 0x00, n * sizeof(char));
/* huffman 树组前面为叶子结点的结构适合使用下面方案实现获取huffman编码 */
/* 从叶子出发反向寻找根结点 */
for(i = 1; i <= n; i++)
{
int current_index = i; // 当前结点索引
int code_index = n-1; // 逆序
int parent_index = ht[i].parent; // 父结点索引
while(parent_index != 0)
{
if(ht[parent_index].left == current_index)
hcc[--code_index] = '0';
else
hcc[--code_index] = '1';
current_index = parent_index;
parent_index = ht[current_index].parent;
}
hc[i] = (char *)malloc((n-code_index)*sizeof(char)); // 多一个空间作为结束符
if(hc[i] == NULL)
{
for(int j=0; j < i; j++)
free(hc[j]);
free(hc);
free(hcc);
return HT_ERROR;
}
strncpy(hc[i], &hcc[code_index], n-code_index); // 最后一个为 0x00，即是‘\0’
}
free(hcc);
*hc_ptr = hc;
return HT_OK;
}
