【数据结构&算法】10-串基础&KMP算法源码
目录
前言
李柱明博客：https://www.cnblogs.com/lizhuming/p/15487367.html
串的定义
定义：
- 串（string）：由零个或多个字符组成的有限序列，又名叫字符串。
相关概念：
-
空格串：只包含空格的串。
- 注意：与空串区别，空格串是有内容有长度的，而且可以不止一个空格。
-
子串：串中任意个数的连续字符组成的子序列，称为该串的子串。
-
主串：相应地，包含子串的串，称为主串。
-
子串在主串中的位置：子串的第一个字符在主串中的序号。
串的比较
串的比较：
- 通过组成串的字符之间的编码来进行的。
- 而字符的编码：指的是字符在对应字符集中的序号。
ASCII 和 Unicode：
- ASCII 码：用 8 个二进制数表示一个字符，总共可以表示 256 个字符。
- Unicode 码：用 16 位二进制数表示一个字符，总共有 2 的 16 次方 个字符。
- 为了和 ASCII 码兼容，Unicode 码的前 256 个字符与 ASCII 码完全相同。
串相等：
- 长度相等，各个对应位置的字符相等。
串的抽象类型数据
串与线性表的比较
线性表：更关注单个元素的操作，如查找一个元素，插入或删除一个元素。
串：更多是查找子串位置、得到指定位置子串、替换子串等操作。
串的数据
数据：串中元素仅由一个字符组成，相邻元素具有前驱和后继关系。
操作：
str_assign(t, *cahrs);生成一个其值等于字符串常量 chars 的串 t。str_copy(t, s);串 s 存在，由串 s 复制得到串 t 中。str_clear(s);清空串。str_empty(s);判断串是否空。str_length(s);串的长度。str_compare(s, t);若 s>t，返回 >0 ， 若 s=t ，返回 0 ，若 s<t ，返回 <0。str_concat(t, s1, s2);合并 s1 和 s2，通过 t 返回。str_get_sub(t, s, pos, len);在串 s 中从 pos 点开始截取最大 len 的长度，通过 t 返回。str_index(s, t, pos);在主串 s 的 pos 位置起查找子串 t 并返回起始子串起始位置，没有则返回 0。str_replace(s, t, v);在主串 s 中查找子串 t，并用串 v 代替。str_insert(s, pos, t);在主串 s 的 pos 位置中插入串 t。str_delete(s, pos, len);在主串 s 中的 pos 位置其删除长度为 len 的子串。
串的存储结构
串的存储结构与线性表类似，分为两类：顺序和链式。
串的顺序存储结构
定义：用一组地址连续的存储单元来存储串中的字符序列。
按照预定义大小，为每个定义的串分配一个固定长度的存储区，一般用定长数组来定义。
一般可以将实际的串长值保存在数组的 0 下标位置，或者在数组的最后一个下标位置。
但有的语言规定在串值后面加一个不计入串长度的结束标记符号“\0”来表示串值的终结（但占用一个空间）。
由于过于不便，串的顺序存储操作有一些变化：串值的存储空间可在程序执行过程中动态分配而得
- 比如堆：可由 c 语言动态分配函数 malloc() 和 free()来管理。
串的链式存储结构
定义：用节点保存串的数据。
若一个结点存放一个字符，会存在很大的空间浪费。
故串的链式可以一个结点放多个字符，最后一个结点若不满，可用#或其他非串值字符补全。（每个节点固定长度）
优点：连接两串操作方便。
缺点：灵活度、性能都不如顺序存储结构的。
朴素的模式匹配算法
模式匹配的定义
子串（又称模式串）的定位操作通常称做串的模式匹配，是串中最重要的操作之一。
朴素的匹配方法（BRUTE FORCE 算法，BF 算法）
逻辑思路：
- 对主串的每个字符作为子串开头，与要匹配的字符串进行匹配。
- 对主串做大循环，每个字符开头做要匹配子串的长度的小循环，直到匹配成功或全部遍历完成为止。
数据结构：
typedef struct{
char *str;
int max_length;
int length;
}data_str_t;
代码实现：
int bf_index(data_str_t main_str, int start, data_str_t sub_str)
{
int i = start, j = 0, v;
while ((i < main_str.length)&&(j < sub_str.length))
{
if(main_str.str[i] == sub_str.str[j])
{
i++;
j++;
}
else
{
i = i - j + 1;
j = 0;
}
}
if (j == sub_str.length)
{
v = i-sub_str.length;
}
else
{
v = -1;
}
return v;
}
时间复杂度分析
n：主串长度，m：要匹配子串长度。
时间复杂度分析：
-
最好情况：O(1)
- 第一次比较就找到。
-
平均情况：O(n+m)
- 根据等概率原则，平均是(n+m)/2 次查找。
-
最坏的情况： O(m×n) （注：(n-m+1)×m）
- 每遍比较都在最后出现不等，即每遍最多比较 m 次，最多比较 n-m+1 遍，总的比较次数最多为 m(n-m+1)。
KMP 模式匹配算法
KMP 与 BF 算法
KMP 算法：
- 由三位前辈发表的一个模式匹配算法，可以大大避免重复遍历的情况，称之为克努特-莫里斯-普拉特算法，检查 KMP 算法。
- 又叫 快速模式匹配算法。
KMP 算法相比于 BF 算法，优势在于：
- 在保证指针 i 不回溯的前提下，当匹配失败时，让模式串向右移动最大的距离；
- 并且可以在
O(n+m)的时间数量级上完成对串的模式匹配操作。
KMP 算法原理
参考链接：CSDN
理解：
- 为什么要找最长公共部分？因为 公共部分 就是一样的意思，既然一样，那就不用重复再逐个对比，直接调到差异或未知部分进行对比，这就是最长公共部分的意义。比过就不要再比。
原理：
-
主串 S 与模式串 T 有部分相同子串时，可以简化朴素匹配算法中的循环流程。
-
KMP 中的关键就是求公共最长匹配前缀和后缀的长度。
-
从子串最长前缀和最长后缀开始求。最长也少于前面字符个数。
-
最长公共前缀的后面一个字符（指针 j）和匹配失败的那个字符（指针 i）进行对比。
- 若匹配相同，则继续推荐 i 和 j。
- 若匹配不同，则继续缩短公共最长前缀和后缀。就是指针 j 进行参考 next 数组回溯。
-
-
-
例子 1，如下图：跳过主串和子串相同的部分。
- 前提：要先知道模式串 T 中首字符 ‘a’ 与串 T 后面的字符均不相等。
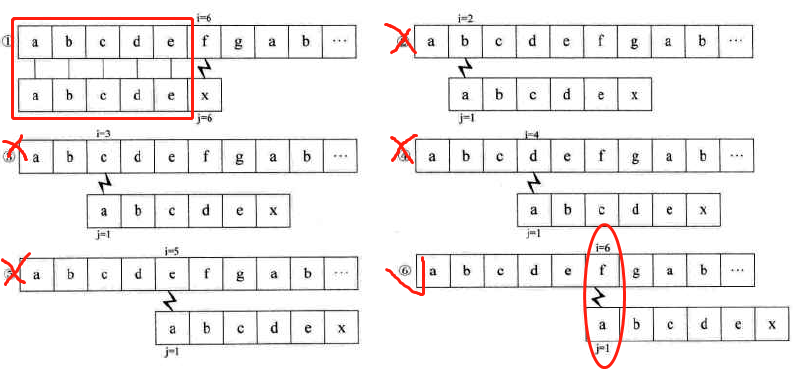
- 前提：要先知道模式串 T 中首字符 ‘a’ 与串 T 后面的字符均不相等。
-
例子二，如下图：跳过子串中与首字符相同的字符。
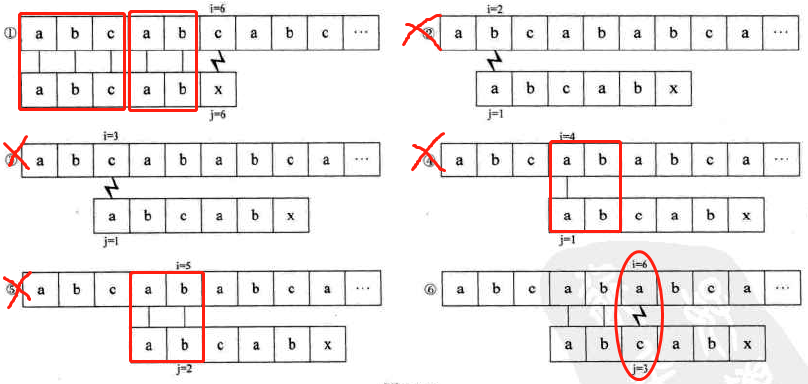
模式串向右移动距离的计算
在模式串和主串匹配时，各有一个指针指向当前进行匹配的字符（主串中是指针 i ，模式串中是指针 j ）。
在保证 i 指针不回溯的前提下，如果想实现功能，就只能让 j 指针回溯。
j 指针回溯的距离，就相当于模式串向右移动的距离。 j 指针回溯的越多，说明模式串向右移动的距离越长。
计算模式串向右移动的距离，就可以转化成：当某字符匹配失败后， j 指针回溯的位置。
模式串中的每个字符所对应 j 指针回溯的位置，可以通过算法得出，得到的结果相应地存储在一个数组中（默认数组名为 next ）。
- 即是模式串中遇到某个字符匹配失败，就在 next 数组中找到对应的回溯位置，取出该位置对应的字符和当前的字符继续匹配，直至全部匹配失败再推进主串指针 i 和模式串指针 j。
计算方法：
-
对于模式串中的某一字符来说，提取它前面的字符串，分别从字符串的两端查看连续相同的字符串的个数，在其基础上 +1 ，结果就是该字符对应的值。
-
注意：
-
next为0，就是拿模式串首个字符的前一个字符和当前主串字符比，意思就是模式串的首个字符和主串的下一个字符比。就是表示需要推进 i 的意思。
- next为1，表示模式串首个字符和主串比。
-
回溯值数组的索引是从1开始的，第一个元素
next[1]是默认设为0的。即是模式串首个字符的回溯值放到next[1]。next[0]没有用到，可以存放 next 数组的长度。
-
模式串前面两个字符对应的回溯值默认为 0、1。
-
例子：求模式串 “abcabac” 的 next 。
- 第 1 个字符：‘a’，next 值为 0。
- 第 2 个字符：‘b’，next 值为 1。
- 第 3 个字符：‘c’，提取字符串 ‘ab’，连续系统字符为 0 个。0 + 1 = 1。 next 值为 1。
- 第 4 个字符：‘a’，提取字符串 ‘abc’，连续系统字符为 0 个。0 + 1 = 1。 next 值为 1。
- 第 5 个字符：‘b’，提取字符串 ‘abca’，连续系统字符为 1 个。1 + 1 = 2。 next 值为 2。
- 第 6 个字符：‘a’，提取字符串 ‘abcab’，连续系统字符为 2 个。2 + 1 = 3。 next 值为 3。
- 第 7 个字符：‘c’，提取字符串 ‘abcaba’，连续系统字符为 1 个。1 + 1 = 2。 next 值为 2。
- 由上的 next 数组的值为（从
next[1]开始） [0, 1, 1, 1, 2, 3, 2]。
代码实现：
-
理解：下图为 demo
-
-
理解字符串和 next 数组的下标都为 1 开始。（可以从 0 开始，自己留意下就可以了，不影响原理）
-
计算 next 数组的值只需要模式串即可，求出每个字符匹配失败时指针 j 回溯的长度。
-
在求 next 数组的值得过程中：
-
不要采用暴力算法检索模式串。
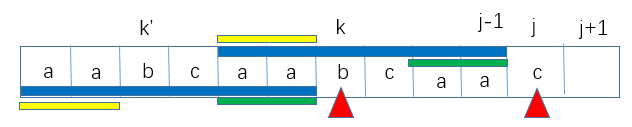
- 即是不要从可能最长的公共前后缀开始一个减一个地对比下去。如求图中 j+1 的 next 值时，暴力算法就是对比 aabcaabcaa 和 abcaabcaab，如果失败就减少一个长度继续重新对比 aabcaabca 和 bcaabcaab。然后循环下去。
-
应该采用 KMP 算法（对，就是在 KMP 算法中利用 KMP 算法思维）检索模式串。
-
即是如求图中 j+1 的 next 值时，直接取出 j 的 next 值 k 对应的字符 b（j 匹配时的最长公共前后缀，从最长的公共前后缀下手），对比 j 和 k 对应的字符。
- 如匹配相同，则 k+1 （在上一个字符的最长公共前后缀基础上在加长一个字符）就是 j+1 对应字符的 next 值。
- 若匹配不同，噢，匹配不同，后缀和前缀匹配时不同噢，主串和模式串匹配时不同噢，那就找出后缀（主串）和前缀（模式串）的公共前后缀，在这里前缀（主串）和后缀（模式串）是一样的，就是找出前缀（模式串）的公共前后缀部分（或者说 k 匹配失败时怎么办，利用 next 回溯啊）。就是找出 k 对应的公共前后缀部分，我们已经求出来了啊，就是
next[k]k'。k' 对应的字符和 j 对应的字符继续对比，若匹配相同，就next[j] = k'+1，若匹配不同就继续缩短最长公共前后缀，最长就是 k' 对应字符的最长公共前后缀next[k']。 - 不说了，这样应该能看出递归了吧。直至最长公共前后缀为 0 时，采用特殊处理，因为这里下标 0 没有对应的字符，所以就推进 i 和 j，就是模式串的首字符和主串的下一个字符继续比较。看代码吧，骚年！！
-
-
-
利用上一个字符对应的 next 值，取出对应的字符，比较当前字符。
-
如果相等。当前字符的 next 值为上一个 next 值 + 1。结束。
-
如果不等，就拿上一个 next 的值做 next 的下标，继续取出字符对比。直至字符相等或循环到 next[1] = 0 结束。
- 循环获取下标 j 就是不断回溯 j。
-
-
-
注意：
- next 数组使用的下标初始值为 1 ，next[0] 没有用到（也可以存放 next 数组的长度）。
- 而串的存储是从数组的下标 0 开始的，所以程序中为 str[i-1] 和 str[j-1]。
-
初版（下面代码只提供思路，具体代码参考最后）：
#include <stdio.h>
#include <string.h>
/**
* @name next_creat
* @brief 简版。时间复杂度O(n)
* @param
* @retval
* @author
*/
void next_creat(char *str, int *next)
{
int i = 1;
next[1] = 0;
int j = 0;
while (i<strlen(str))
{
if (j == 0 || str[j-1] == str[i-1])
{
i++;
j++;
next[i] = j;
}
else
{
j = next[j]; // 指针j，递归回溯。 // 算法重点语句。
}
}
}
-
优化版（下面代码只提供思路，具体代码参考最后）：
-
初版有个弊端，如模式串 caaaaabx。
- 用初版思维推导下，会发现当最后一个 a 匹配失败时需要回溯，但是前面的最长公共前后缀都是-1，不就是和暴力算法一样的效果吗。
- 另外既然最后一个字符 a 匹配不成功，那前面连续的 a 肯定匹配不成功的，所以就应该直接回溯到前面连续字符的前一个字符 c。参考下面代码或者看大话数据结构 P142 页。
-
根据第 j 个的 next 值找它的 next 值 x 对应的第 x 个字符，并判断第 j 个和第 x 个字符是否相等。
-
若不相等，保持 val 值等于 next 值；若相等，val 值等于第 x 个值的 val 值。
-
#include <stdio.h>
#include <string.h>
/**
* @name next_creat
* @brief 优化版。时间复杂度O(n)
* @param
* @retval
* @author
*/
void nextval_creat(char *str, int *nextval)
{
int i = 1;
nextval[1] = 0;
int j = 0;
while (i<strlen(str))
{
if (j == 0 || str[j-1] == str[i-1])
{
i++;
j++;
if(str[i-1] != str[j-1])
nextval[i] = j;/* 如果当前字符和前缀字符不同，则把子串的当前回溯指针j赋值给next */
else
nextval[i] = nextval[j]; /* 如果当前字符和前缀字符相同，则自己采用前缀字符的回溯值 */
}
else
{
j = nextval[j]; // 指针j，递归回溯。
}
}
}
基于 next 的 KMP 算法的实现
KMP 算法（下面代码只提供思路，具体代码参考最后）：
/**
* @name kmp_index
* @brief
* @param
* @retval
* @author
*/
int kmp_index(char *str_main, char *str_sub)
{
int i = 1;
int j = 1;
int next[10];
next_creat(str_sub, next); //根据模式串T,初始化next数组
while (i<=strlen(str_main) && j<=strlen(str_sub))
{
//j==0:代表模式串的第一个字符就和指针i指向的字符不相等；S[i-1]==T[j-1],如果对应位置字符相等，两种情况下，指向当前测试的两个指针下标i和j都向后移
if (j==0 || str_main[i-1] == str_sub[j-1])
{
i++;
j++;
}
else
{
j=next[j];//如果测试的两个字符不相等，i不动，j变为当前测试字符串的next值
}
}
if (j > strlen(str_sub))
{
//如果条件为真，说明匹配成功
return i-(int)strlen(str_sub);
}
return -1;
}
KMP 时间复杂度
KMP 算法的时间复杂度：O(m+n)
- get_next 的时间复杂度：O(m)
- while 循环的时间复杂度：O(n)
参考代码
串 & KPM 算法
/** @file string_kmp.c
* @brief 采用kmp算法
* @details 详细说明
* @author lzm
* @date 2021-09-11 20:10:56
* @version v1.0
* @copyright Copyright By lizhuming, All Rights Reserved
* @blog https://www.cnblogs.com/lizhuming/
*
**********************************************************
* @LOG 修改日志:
**********************************************************
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define STRING_SIZE 100
/* status_e是函数的类型,其值是函数结果状态代码，如OK等 */
typedef enum {
LZM_STRING_STATUS_ERR = -1,
LZM_STRING_STATUS_OK,
LZM_STRING_STATUS_FALSE,
}status_e;
typedef int elem_type; /* elem_type类型根据实际情况而定，这里假设为int */
typedef char string_t[STRING_SIZE+1];
/**
* @name str_assing
* @brief 生成一个其值等于 str_t 的串 str_s
* @param
* @retval
* @author lzm
*/
status_e str_assing(string_t str_s, char *str_t)
{
int i = 0;
if(str_t == NULL || str_s == NULL || strlen(str_s) > STRING_SIZE)
return LZM_STRING_STATUS_ERR;
else
{
str_t[0] = strlen(str_s);
for(i = 1; i <= str_t[0]; i++)
str_t[i] = *(str_s + i-1);
return LZM_STRING_STATUS_OK;
}
}
/**
* @name str_copy
* @brief 复制串 str_t 到串 str_s
* @param
* @retval
* @author lzm
*/
status_e str_copy(string_t str_s, string_t str_t)
{
int i = 0;
if(str_s == NULL || str_t == NULL)
{
return LZM_STRING_STATUS_ERR;
}
for(i = 0; i <= str_t[0]; i++)
{
str_s[i] = str_t[i];
}
return LZM_STRING_STATUS_OK;
}
/**
* @name str_empty
* @brief 判空
* @param
* @retval
* @author lzm
*/
status_e str_empty(string_t str_t)
{
if(str_t == NULL)
{
return LZM_STRING_STATUS_ERR;
}
if(str_t[0] == 0)
return LZM_STRING_STATUS_OK;
return LZM_STRING_STATUS_FALSE;
}
/**
* @name str_compare
* @brief
* @param
* @retval str_s > str_t 则返回大于0，等就0， 小就负
* @author lzm
*/
int str_compare(string_t str_s, string_t str_t)
{
int i = 0;
if(str_t == NULL || str_s == NULL)
{
return LZM_STRING_STATUS_ERR;
}
for(i = 1; i <= str_s[0] && i <= str_t[0]; ++i)
if(str_s[i] != str_t[i])
return str_s[i] - str_t[i];
return str_s[0] - str_t[0];
}
/**
* @name str_length
* @brief 获取长度
* @param
* @retval
* @author lzm
*/
int str_length(string_t str_s)
{
if(str_s == NULL)
{
return LZM_STRING_STATUS_ERR;
}
return str_s[0];
}
/**
* @name str_clear
* @brief 清空
* @param
* @retval
* @author lzm
*/
int str_clear(string_t str_s)
{
if(str_s == NULL)
return LZM_STRING_STATUS_ERR;
str_s[0] = 0;
return LZM_STRING_STATUS_OK;
}
/**
* @name str_concat
* @brief 拼接
* @param
* @retval
* @author lzm
*/
int str_concat(string_t str_t, string_t str_s1, string_t str_s2)
{
int i = 0;
if(str_t == NULL || str_s1 == NULL || str_s2 == NULL)
return LZM_STRING_STATUS_ERR;
if(str_s1[0] + str_s2[0] <= STRING_SIZE)
{
/* 未截断 */
for(i=1; i<=str_s1[0]; i++)
str_t[i] = str_s1[i];
for(i=1; i <= str_s2[0]; i++)
str_t[str_s1[0]+i]=str_s2[i];
str_t[0] = str_s1[0] + str_s2[0];
return LZM_STRING_STATUS_OK;
}
else if(str_s1[0] <= STRING_SIZE)
{
/* 截断S2 */
for(i=1; i <= str_s1[0]; i++)
str_t[i] = str_s1[i];
for(i=1;i<=STRING_SIZE-str_s1[0]; i++)
str_t[str_s1[0]+i] = str_s2[i];
str_t[0] = STRING_SIZE;
return LZM_STRING_STATUS_FALSE;
}
else
{
return LZM_STRING_STATUS_ERR;
}
}
/**
* @name str_insert
* @brief 插串str_t入串str_s
* @param
* @retval
* @author lzm
*/
int str_insert(string_t str_s, string_t str_t, int pos)
{
int i = 0;
if(str_t == NULL || str_s == NULL || pos < 1 || pos > str_t[0]+1)
{
return LZM_STRING_STATUS_ERR;
}
if(str_s[0] + str_t[0] <= STRING_SIZE)
{
/* 完全插入 */
for(i=str_s[0]; i>=pos; i--)
str_s[i+str_t[0]]=str_s[i]; // 先挪动str_s串腾出空间
for(i=pos; i<pos+str_t[0]; i++)
str_s[i] = str_t[i-pos+1];
str_s[0] = str_s[0] + str_t[0];
return LZM_STRING_STATUS_OK;
}
else
{
/* 部分插入 */
for(i = STRING_SIZE; i<=pos; i--)
str_s[i] = str_s[i-str_t[0]];
for(i=pos; i<pos+str_t[0]; i++)
str_s[i] = str_t[i-pos+1];
str_s[0]=STRING_SIZE;
return LZM_STRING_STATUS_FALSE;
}
}
/**
* @name str_delete
* @brief 删除部分
* @param
* @retval
* @author lzm
*/
int str_delete(string_t str_s, int pos, int len)
{
int i = 0;
if(str_s == NULL || pos < 1 || pos > str_s[0]-len+1)
return LZM_STRING_STATUS_ERR;
for(i=pos+len;i<=str_s[0];i++)
str_s[i-len] = str_s[i];
str_s[0]-=len;
return LZM_STRING_STATUS_ERR;
}
/**
* @name next_creat
* @brief 优化版。时间复杂度O(n)
* @param
* @retval
* @author
*/
int nextval_creat(char *str, int *nextval)
{
int i = 1;
int j = 0;
int len = strlen(str);
if(str == NULL || nextval == NULL)
return LZM_STRING_STATUS_ERR;
nextval[1] = 0; /* 首个字符的next值默认为0。nextval[0]没有用，可以用来存一些数据，如模式串长度 */
while (i<len)
{
/* 遍历算出第 i 个字符的next值。 */
if (j == 0 || str[j-1] == str[i-1])
{
/* j==0：到了需要推进 i ，然后重新对比模式串的地步了，让主串下一个字符和模式串首个字符对比。 */
/* str[j-1] == str[i-1]：主串的字符和最长公共位置的字符一样，也可以推进 i，对比下一个。 */
/* 可以把这个j对应的字符下标记录到next了；顺便对比下一个 */
i++;
j++;
if(str[j-1] != str[i-1]) /* 不一样才有可比性，因为一样，说明和实际主串字符不一样 */
{
nextval[i] = j;/* 如果当前字符和前缀字符不同，直接更新i的回溯值为j */
}
else
{
/*主 xxxxxxxxxxxxxxxxxx[i++]xxxxxxx */
/*模 abcabc...abcabc[i][i++]xxxx */
/*模 abcabc[j][j++]xxxx */
/* 当要求[i++]的next值时，就是[i++]和主串不一样时，我们应该拿哪个字符和主串[i++]继续比？
这里比到[i]和[j]一样，那就本来应该拿[j++]和[i++]继续比的（就是说[j++]这个字符的下标就是next值），
但是优化点就是，如果模式串[j++]和模式串[i++]一样，说明模式串[j++]也和主串[i++]不一样，那对比了后还是要走[j++]不一样的KMP算法，那干嘛不直接把这次模式串[i++]的next值用[j++]的next值呢？直接走[j++]不一样时的kmp算法值更加直接 */
/* 解决更细的重复比较问题。如aaaaab中的b，next应该为0，而不是为5 */
/* 我们本来想拿j来和主串匹配的，但是j和i一样了，而i和主串的值不一样（因为算的就是i的next值），也就说明拿这个j和主串比，那也是不一样的，所以直接按照j不一样来回溯，就是那之前算好的j的next值，所以直接用j的回溯值也是一样的。 */
nextval[i] = nextval[j]; /* 如果当前字符和前缀字符相同，则自己采用前缀字符的回溯值 */
}
}
else
{
/* i和j的字符不一样，那用j的回溯再和i比较 */
j = nextval[j]; // 指针j，递归回溯。
}
}
return LZM_STRING_STATUS_OK;
}
/**
* @name str_kmp_index
* @brief
* @param
* @retval
* @author
*/
int str_kmp_index(string_t str_main, string_t str_sub, int pos)
{
int i = 1;
int j = 1;
int *nextval = NULL;
if(str_main == NULL || str_sub == NULL || pos < 1 || pos > str_main[0] + 1)
return LZM_STRING_STATUS_ERR;
nextval = (int *)malloc(str_sub[0]);
if(nextval == NULL)
return LZM_STRING_STATUS_ERR;
nextval_creat(str_sub, nextval); //根据模式串str_sub,初始化nextval数组
while (i<=strlen(str_main) && j<=strlen(str_sub))
{
//j==0:代表模式串的第一个字符就和指针i指向的字符不相等；S[i-1]==T[j-1],如果对应位置字符相等，两种情况下，指向当前测试的两个指针下标i和j都向后移
if (j==0 || str_main[i-1] == str_sub[j-1])
{
i++;
j++;
}
else
{
j=nextval[j];//如果测试的两个字符不相等，i不动，j变为当前测试字符串的next值
}
}
if (j > strlen(str_sub))
{
//如果条件为真，说明匹配成功
return i-(int)strlen(str_sub);
}
return LZM_STRING_STATUS_ERR;
}
/**
* @name str_replace
* @brief 删除部分
* @param
* @retval
* @author lzm
*/
int str_replace(string_t str_s, string_t str_t, string_t str_v)
{
int i = 0;
if(str_s == NULL || str_t == NULL || str_empty(str_v) != LZM_STRING_STATUS_OK)
return LZM_STRING_STATUS_ERR;
do
{
i = str_kmp_index(str_s, str_t, i); /* 结果i为从上一个i之后找到的子串T的位置 */
if(i) /* 串str_s中存在串str_t */
{
str_delete(str_s, i, str_length(str_t)); /* 删除该串str_t */
str_insert(str_s, str_v, i); /* 在原串str_t的位置插入串str_v */
i+=str_length(str_v); /* 在插入的串str_v后面继续查找串str_t */
}
}
while(i);
return LZM_STRING_STATUS_OK;
}
