欧拉函数
定义
\(1-N\)中与 \(N\) 互质的个数被称为欧拉函数,记为 \(φ(n)\)。
公式
设 \(n={p_1}^{c_1}*{p_2}^{c_2}*\cdots*{p_m}^{c_m}\)
则 \(φ(n)=n*\dfrac{p_1-1}{p_1}*\dfrac{p_2-1}{p_2}*\cdots*\dfrac{p_m-1}{p_m}\)
性质
- \(φ(1)=1\),
因为 \(1\) 的质因数个数为 \(0\),
所以 原式\(=1\) - \(n\) 为质数, 则 \(φ(n)=n-1\),
因为 原式\(=n*\dfrac{n-1}{n}=n-1\) - \(n\) 为质数,则 \(φ(n^k)=(n-1)*n^{k-1}\),
因为 原式\(=n^k*\dfrac{n-1}{n}=n^{k-1}*(n-1)\) - 当 \(n,m\) 互质,\(φ(n*m)=φ(n)*φ(m)\),
因为如果设
\(n={p_1}^{c_1}*{p_2}^{c_2}*\cdots*{p_x}^{c_x}\),
\(m={q_1}^{d_1}*{q_2}^{d_2}*\cdots*{q_y}^{d_y}\),
则 \(φ(n*m)=n*m*\dfrac{p_1-1}{p_1}*\dfrac{p_2-1}{p_2}*\cdots*\dfrac{p_x-1}{p_x}*\dfrac{q_1-1}{q_1}*\dfrac{q_2-1}{q_2}*\cdots*\dfrac{q_y-1}{q_y}\)
\(=n*\dfrac{p_1-1}{p_1}*\dfrac{p_2-1}{p_2}*\cdots*\dfrac{p_x-1}{p_x}*m*\dfrac{q_1-1}{q_1}*\dfrac{q_2-1}{q_2}*\cdots*\dfrac{q_y-1}{q_y}\)
\(=φ(n)*φ(m)\) - \(n\) 为质数,\(\begin{cases}p\%n=0,φ(p*n)=φ(p)*n\\p\%n\neq0,φ(p*n)=φ(p)*(n-1)\end{cases}\)
因为,第二条由④与②得。而当 \(n\%p=0\) 时,每增加 \(n\) 就会少一个互质数,所以最终少 \(φ(n)\) 个。 - 当 \(n>1\) 时 ,\(s=1-n\) 与 \(n\) 互质的整数和 \(=n*φ(n)/2\)
令 \(x<n,gcd(x,n)=1\) 则 \(gcd(n,n-x)\) ,所以 \(x∈\{1,a2,\cdots ,a*φ(n)/2,- n-a*φ(n)/2,\cdots,n-a2,n-1\}\) ,等差数列得 \(n*φ(n)/2\) - \(\sum_{d|n} φ(d)=n\)
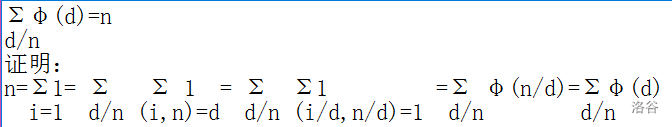
同余
定义
当 \(a\%m=b\%m\) 时,我们称 \(a,b\) 关于 \(mod\) \(m\) 同余。记作 \(a\equiv b\pmod{m}\)。
定理
\(a\equiv b\pmod{m}\) ,当且仅当 \(m|(a-b)\)。
\(a\equiv b\pmod{m}\) ,当且仅当存在整数 \(k\),使得 \(a=b+k*m\)。
性质
1、自反性:\(a≡a\pmod m\)
2、对称性:若 \(a ≡ b\pmod m\),则 \(b ≡ a\pmod m\)
3、传递性:若 \(a ≡ b\pmod m\),\(b ≡ \pmod m\),则 \(a ≡ c\pmod m\)
4、同加性:若 \(a ≡ b\pmod m\),则 \(a+c ≡ b+c\pmod m\)
5、同乘性:若 \(a ≡ b\pmod m\),则 \(a*c ≡ b*c\pmod m\)
6、同幂性:若 \(a ≡ b\pmod m\),则 \(a^n ≡ b^n\pmod m\)
7、若 \(a \% p=x,a \% q=x,\gcd(p,q)=1\),则\(a \%(p*q)=x\)
欧拉定理
当 \(gcd(a,m)=1\) ,会有 \(a^{\varphi(m)}≡1\pmod m\)。
证明:
既约剩余系:所有关于 \(m\) 同余的数组成的集合称为模 \(m\) 的一个剩余类。在模 \(m\) 的每个互质剩余类中任取一数,我们称所有的数所组成的集为模 \(m\) 的一个既约剩余系,项数为 \(\varphi(m)\)。
设 \(S=\{b_1,b_2,\cdots b_{\varphi (m)}\}\) 为模 \(m\) 的一个既约剩余系。
因为 \(gcd(a,m)=1,gcd(b_i,m)=1(1 \le i \le \varphi (m))\)
所以 \(S'=\{a*b_1,a*b_2,\cdots a*b_{\varphi (m)}\}\) 也为模 \(m\) 的一个既约剩余系,\(S=S'\)。
所以 \(S≡S'\pmod m\)
\(\prod_{i=1}^{φ(m)}b_i ≡ \prod_{i=1}^{φ(m)}(a*b_i)\pmod m\)
$ \prod_{i=1}^{φ(m)}(a*b_i) ≡ \prod_{i=1}^{φ(m)}b_i\pmod m$
\(m|\prod_{i=1}^{φ(m)}(a*b_i)-\prod_{i=1}^{φ(m)}b_i\pmod m\)
\(m|(a^{φ(m)}-1)\prod_{i=1}^{φ(m)}b_i\pmod m\)
因为 \(S\) 为模 \(m\) 的一个既约剩余系
所以 \(m|\prod_{i=1}^{φ(m)}b_i\pmod m\)
所以 \(m|(a^{φ(m)}-1)\pmod m\)
\(a^{φ(m)}-1≡0\pmod m\)
\(a^{φ(m)}≡1\pmod m\)
费马小定理
当 \(p\) 为质数,\(a^p≡a\pmod p\)。
证明:
当 \(\gcd(p,a)=1\) ,根据欧拉定理,\(a^{φ(p)}≡1\pmod p\)
因为 \(φ(p)=p-1\)
所以 \(a^{p-1}≡1\pmod p\)
\(a^p≡a\pmod p\)
当 \(\gcd(p,a)\neq 1\),即 \(a\) 为 \(p\) 的倍数。
所以 \(a^p|p,a|p\)
所以 \(a^p≡a\pmod p\)
扩展欧几里得
贝祖定理
对于任意整数 \(a,b\) 存在整数 \(x,y\),满足 \(ax+by=\gcd(a,b)\)
在辗转相除中求解:\(a*x+b*y=\gcd(a,b)=\gcd(b,a\%b)=b*x'+(a\%b)*y'\)
\(=b*x'+(a-\lfloor\dfrac{a}{b}\rfloor*b)*y'\)
\(=b*x'+a*y'-\lfloor\dfrac{a}{b}\rfloor*b*y'\)
\(=a*y'+b*(x'-\lfloor\dfrac{a}{b}\rfloor*y')\)
所以 \(x=y'\),\(y=x'-\lfloor\dfrac{a}{b}\rfloor*y'\)。递归求解
通解:
设辗转相除中的解为 \(x_0,y_0\) ,则通解满足:
\(x=x_0+b/\gcd(a,b)*t\)
\(y=y_0-a/\gcd(a,b)*t\)
\(t\) 为任意整数
证明:
设 \(x=x_0+k_1,y=y_0+k_2\)
则 \(a*x_0+a*k_1+b*y_0+b*k_2=\gcd(a,b)\)
\(a*k_1+b*k_2=0\)
有特殊解 \(k_1=b,k_2=-a\)
有最小解 \(k_{1_0}=\dfrac{b}{\gcd(a,b)},k_{2_0}=\dfrac{a}{\gcd(a,b)}\)
其他解扩倍则 \(t*(\dfrac{b}{\gcd(a,b)}+\dfrac{a}{\gcd(a,b)})=0\)
所以 \(x=x_0+b/\gcd(a,b)*t\),\(y=y_0-a/\gcd(a,b)*t\)
最小非负整数解:
\(x_0\) 每次移动 \(b/\gcd(a,b)\) 单位,最终 \(x_0-b/\gcd(a,b)*i>0\) 并且 \(x_0-b/\gcd(a,b)*(i+1)<0\)。
则 \(x=(\underline{x_0\%(b/\gcd(a,b)}+\underline{b/\gcd(a,b))\%(b/\gcd(a,b))}\)
(限定范围)(取非负)
解方程 \(ax+by=n\)
条件:\(\gcd(a,b)|n\)
过程:
- 扩欧求得 \(ax+by=gcd(a,b)\) 的解 \(x_0,y_0\)
- 求得原方程特解 \(x_1=x_0*n/\gcd(a,b),y_1=y_0*n/\gcd(a,b)\)
- 套用通解 \(x=x_1+b/\gcd(a,b)*t\) \(y=y_1-a/\gcd(a,b)*t\)
线性同余方程
基本形式:\(a*x≡\pmod m\)
条件:\(\gcd(a,m)|b\)
转化:\(a*x≡b\pmod m ->m|(a*x-b)->a*x-m*y=b->a*x+m*y=b\)
逆元
定义:当 \(\gcd(m,b)=1\) 且 \(b|a\),则有整数 \(x\) ,满足 \(\dfrac{a}{b}≡a*x\pmod m\) ,称 \(x\) 为 \(b\) 的模 \(m\) 乘法逆元,记为 \(b^{-1}\pmod m\)。
扩欧求逆元:
当 \(\gcd(a,m)=1\) 时,
\(\dfrac{a}{b}≡\dfrac{a}{b}*b*b^{-1}\pmod m\)
\(1≡b*x\pmod m\)
解方程
费马小求逆元:
当 \(m\) 为质数,\(b<m\) 时,由费马小定理得 \(b^m≡b\pmod m\)
\(b^{m-1}≡1\pmod m\)
\(b*b^{m-2}≡1\pmod m\)
\(x=b^{m-2}\)
递推求逆元:
当 \(i<p\),\(p\) 为质数时,\(p=k*i+r\),其中 \(k=p/i,r=p\%i\)
\((k*i+r)≡0\pmod p\)
\((k*i*i^{-1}+r*i^{-1}) ≡0\pmod p\)
\(r*i^{-1} ≡-k\pmod p\)
\(i^{-1} ≡-k*r^{-1}\pmod p\)
\(i^{-1} ≡-(p/i)(p\%i)^{-1}\pmod p\)
\(i^{-1} ≡(p-p/i)(p\%i)^{-1}\pmod p\)
则 \(ny_i=(p-p/i)*ny_{p\%i}\%p\)
中国剩余定理
CRT
定义:
\(\begin{cases}x≡a_1\pmod {m_1}\\x≡a_2\pmod {m_2}\\\cdots\\x≡a_n\pmod {m_n}\end{cases}\)
当 \(m_1,m_2,\cdots,m_n\) 两两互质,\(\dfrac{\prod_{i=1}^{n}m_i}{m_i}*t_i≡a_i\pmod {m_i}\),解为 \(x=\sum_{i=1}^n (a_i*t_i*\dfrac{\prod_{i=1}^{n}m_i}{m_i})\)
证明:
当 \(m_1,m_2,\cdots,m_n\) 两两互质:
设 \(m_{i_{lcm}}=lcm(m_1,m_2,\cdots,m_n)/m_i=\dfrac{\prod_{i=1}^{n}m_i}{m_i}\)
则 \(m_{i_{lcm}}*t_i≡a_i\pmod {m_i}\)
\(m_{i_{lcm}}*(t_i/a_i)≡1\pmod {m_i}\)
解出 \((t_i/a_i)\)
则该方程最终的解为 \(m_{i_{lcm}}*(t_i/a_i)*a_i\)
则最终解为 \(x=\sum_{i=1}^n (a_i*t_i*m_{i_{lcm}})\)
EXCRT
定义:
\(\begin{cases}x≡a_1\pmod {m_1}\\x≡a_2\pmod {m_2}\\\cdots\\x≡a_n\pmod {m_n}\end{cases}\)
求解的过程
过程:
从第一个方程开始,逐个满足
设 \(m=lcm(m_1,m_2,\cdots,m_i)\) ,初始 \(x_1=a_1\) 。
则 \(x+t*m\) 是前 \(i-1\) 个方程的解。
当前方程满足 \(x_{i-1}+t'*m≡a_i\pmod {m_i}\)
即 \(t'*m≡a_i-1\pmod {m_i}\)
求解或无解,若有解,则 \(x_i=x_{i-1}+t'*m\)
最终输出 \(x_n\)

Catalan 数
定义:将 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 按照某种顺序排成长度为2n的序列,满足任意前缀 \(0\) 的个数都不少于 \(1\) 的个数的序列的数量。
组合公式:\(Cat_n=\dfrac{1}{n+1}*C^{n}_{2n}\)
证明:
\(n\) 个 \(0\) 和 \(n\) 个 \(1\) 组成的排列个数为 \(C^{n}_{2n}\)。
对于一个由 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 组成的序列,必然有一个前缀有 \(p\) 个 \(0\) ,\(p+1\) 个 \(1\)。对于一个由 \(n'-1\) 个 \(0\) 和 \(n'+1\) 个 \(1\) 组成的序列,也必然存在一个前缀有 \(p'\) 个 \(0\) ,\(p'+1\) 个 \(1\)。所以由 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 组成的序列和由 \(n'-1\) 个 \(0\) 和 \(n'+1\) 个 \(1\) 组成的序列一一对应。由 \(n'-1\) 个 \(0\) 和 \(n'+1\) 个 \(1\) 组成的序列有 \(\dfrac{(2n)!}{(n-1)!*(n+1)!}=C^{n-1}_{2n}\),则:\(Cat_n=C^{n}_{2n}-C^{n-1}_{2n}=\dfrac{(2n)!}{n!*n!}-\dfrac{(2n)!}{(n-1)!*(n+1)!}=\dfrac{1}{n+1}*C^{n}_{2n}\)
递推公式:\(Cat_n=\dfrac{4n-2}{n+1}*Cat_{n-1}\)
证明:
\(Cat_n-Cat_{n-1}=(\dfrac{1}{n+1}*C^{n}_{2n})/(\dfrac{1}{n}*C^{n-1}_{2n-2})\)
\(=\dfrac{1}{n+1}*C^{n}_{2n}*\dfrac{1}{n}/C^{n-1}_{2n-2}\)
\(=\dfrac{1}{n+1}*\dfrac{(2n)!}{n!*n!}*\dfrac{1}{n}/\dfrac{(2n-2)!}{(n-1)!*(n-1)!}\)
\(=\dfrac{4n-2}{n+1}\)
所以 \(Cat_n=\dfrac{4n-2}{n+1}*Cat_{n-1}\)
概率与数学期望
随机试验
条件:
- 试验可以在相同条件下重复进行
- 试验可能出现的结果有多个,试验之前知道所有可能的结果
- 试验结束后会出现哪一个结果是随机的
定义:
- 基本事件(\(ω\)):一次试验可能出现的每一个直接的结果,也就是随机试验不能够再分解的结果。
- 样本空间(\(Ω\)):全体基本事件的集合。
- 标记:每个事件使用大写字母标记。
- 事件发生:事件 \(A\) 中包含的任意基本时间发生,我们称事件 \(A\) 发生。
- 必然事件:必然发生的事件(\(Ω\))。
- 不可能事件:必然不发生的事件(\(Φ\))。
运算:
- \(A⊂B\) 或 \(B⊃A\) : 事件 \(A\) 发生必然导致事件 \(B\) 发生。
- \(A\cup B\) 或 \(A+B\):事件 \(A\) 与事件 \(B\) 至少有一个发生。
- \(A\cap B\) 或 \(A*B\):事件 \(A\) 与事件 \(B\) 同时发生。
- \(A-B\):事件 \(A\) 发生而事件 \(B\) 不发生。
- \(B=A\) 或 \(A=B\):事件 \(A\) 与事件 \(B\) 不能同时发生。(\(A\cap B=Φ,A\cup B=Ω\))
- \(A|B\):\(A\) 和 \(B\) 为两事件,且 \(P(A)>0\),则称 \(P(A*B)/P(A)\) 为事件 \(A\) 发生的条件下事件 \(B\) 发生的条件概率,记作 \(P(B|A)\),即 \(P(B|A)= P(A*B)/P(A)\)
离散概率模型
定义:
- 试验中所有可能出现的基本事件只有有限个。
- 试验中每个基本事件出现的可能性相等。
公式:
设 \(A\) 由 \(m\) 个基本事件组成,共 \(n\) 个基本事件
则发生 \(A\) 的概率 \(P(A)=\dfrac{m}{n}\)
连续概率模型
定义:
- 试验中所有可能出现的基本事件有无限个。
- 试验中每个基本事件出现的可能性相等。
公式:
设 \(A\) 长 \(m\) ,共长 \(n\) 。
则发生 \(A\) 的概率 \(P(A)=\dfrac{m}{n}\)
公式
划分:
\(A_1,A_2,\cdots,A_n\) 为样本空间 \(S\) 的划分当:
- \(U_{i=1}^na_i=S\)
- \(A_i*A_j=Φ(1 \le i,j \le n,i\neq j)\)
全概率公式:
设 \(A_1,A_2\cdots,A_n\) 为 \(S\) 的一个划分且 \(P(A_i)>0\),则:
\(P(A)\)
\(=\sum_{i=1}^nP(A*B_i)\)
\(=\sum_{i=1}^nP(B_i)*P(A|B_i)\)
贝叶斯公式:
\(P(A_j|B)=\dfrac{P(A_j*B)}{P(B)}=\dfrac{P(A_j)*P(B)}{\sum_{i=1}^nP(A_i)*P(B|A_i)}(1 \le i \le n)\)
数学期望
定义:设 \(X\) 为离散的随机边量,它的值为 \(X_i(1 \le i \le n)\) 的概率为 \(P_i\) 。则数学期望 \(E[X]=\sum_{i=1}^n(X_i*P_i)\)
性质:
- \(E[X+c]=E[X]+c\)
- \(E[X*c]=E[X]*c\)
- \(E[X+Y]=E[X]+E[Y]\)
- \(E[aX+bY]=aE[X]+bE[Y]\)
方差
定义:“期望值离散程度”的期望值
公式:设 \(X\) 为离散的随机边量,它的值为 \(X_i(1 \le i \le n)\) 的概率为 \(P_i\) 。则方差 \(V[X]=E[(X-\mu)^2]=\sum_{i=0}^nP(x_i)*(x_i-\mu)^2\)。其中 \(\mu=E[X]\)
性质:
- \(V[X+c]=V[X]\)
- \(V[X*c]=c^2*V[x]\)
- \(V[X]=E[X^2]-E[X]^2\)


