[数据结构]克鲁斯卡尔（Kruskal）算法

算法的概念

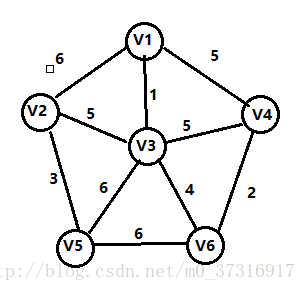
　　与Prim算法从顶点开始扩展最小生成树不同，Kruskal算法是一种按权值的递增次序选择合适的边来构造最小生成树的方法。假设N=（V,E）是连通网，对应的最小生成树T=（Vt，Et），Kruskal算法的步骤如下：
　　初始化：Vt=V，Et=空集。即每个顶点构成一棵独立的树，T此时是一个仅含|V|个顶点的森林；
　　循环（重复下列操作至T是一棵树）：按G的边的权值第怎顺序依次从E-Et中选择一条鞭，如果这条边加入T后不构成回路，则将其加入Et，否则舍弃，直到Et中含有n-1条边。

实例及解析

第一步：

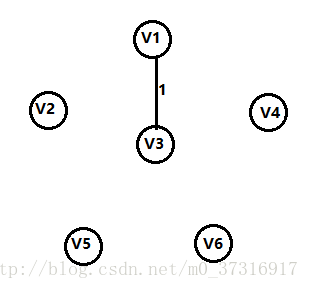
从上面介绍的步骤可以看出，按权值递增的顺序添加边，从这个例子中可以看出1是最短的边，加入集合E
第二步：

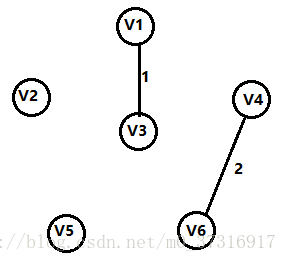
还是上面的原则，加入一条权值最短的边，并且不能构成回路，所以添加V4,V6的边。
第三步：

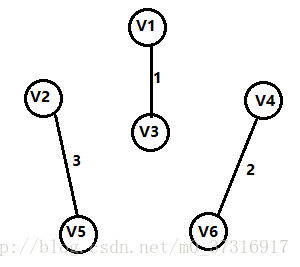
还是上面的原则，加入一条权值最短的边，并且不能构成回路，所以添加V2,V5的這条边。
第四步：

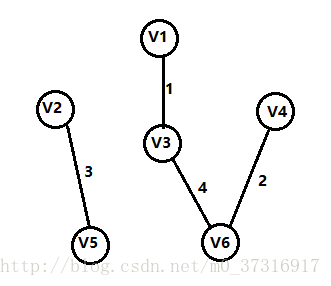
还是上面的原则，加入一条权值最短的边，并且不能构成回路，所以添加V3,V6的這条边。
第五步：

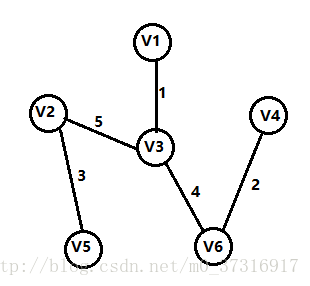
这一步很重要！我们会发现图中有3条权值为5的边，那我们应该如何选择呢？有一个很重要的原则就是添加这条边之后，生成树不能构成回路，如果添加V3,V4或者V1,V4这两条边的话就会构成回路，所以我们只能选择V2到V3的这条边；此时，最小生成树已经形成。

总结：通过kruskal算法和prim算法的比较我们可以发现一个最大的区别：Prim算法要求每次添加一条边，都要集合中所有的顶点都是连通状态的，而kruskal算法却没有这样的要求，它只需要每条边的权值都是从小往大递增选择的；而两个算法共同点就是要求：加入这条边之后，顶点集合不能构成一个回路。

伪代码

void Kruskal(V,T){
    T=V;
    numS=n;
    while(numS>1){
    从E中取出权值最小的边（v，u）;
    if(v和u属于T中不同的连通分量){
    T=T∪{（v，u）};//将此边加入生成树中
    numS--;//不连通分量树减1
    }
    }
}

算法复杂度

　　通常在kruskal算法中，采用堆来存放边的集合，则每次选择最小权值的边只需要O（log|E|）的时间。(按小根堆存放，每次从堆顶取值，每次调整堆只需要logn的复杂度)。由于按照最小堆存放，所以建堆的时间为O（n），需要进行n-1次向下调整的操作，每次调整时间为O(logn)，所以总的时间复杂度为O(nlogn)，也就是O(ElogE)。