最小生成树

　　最小生成树的定义：一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。

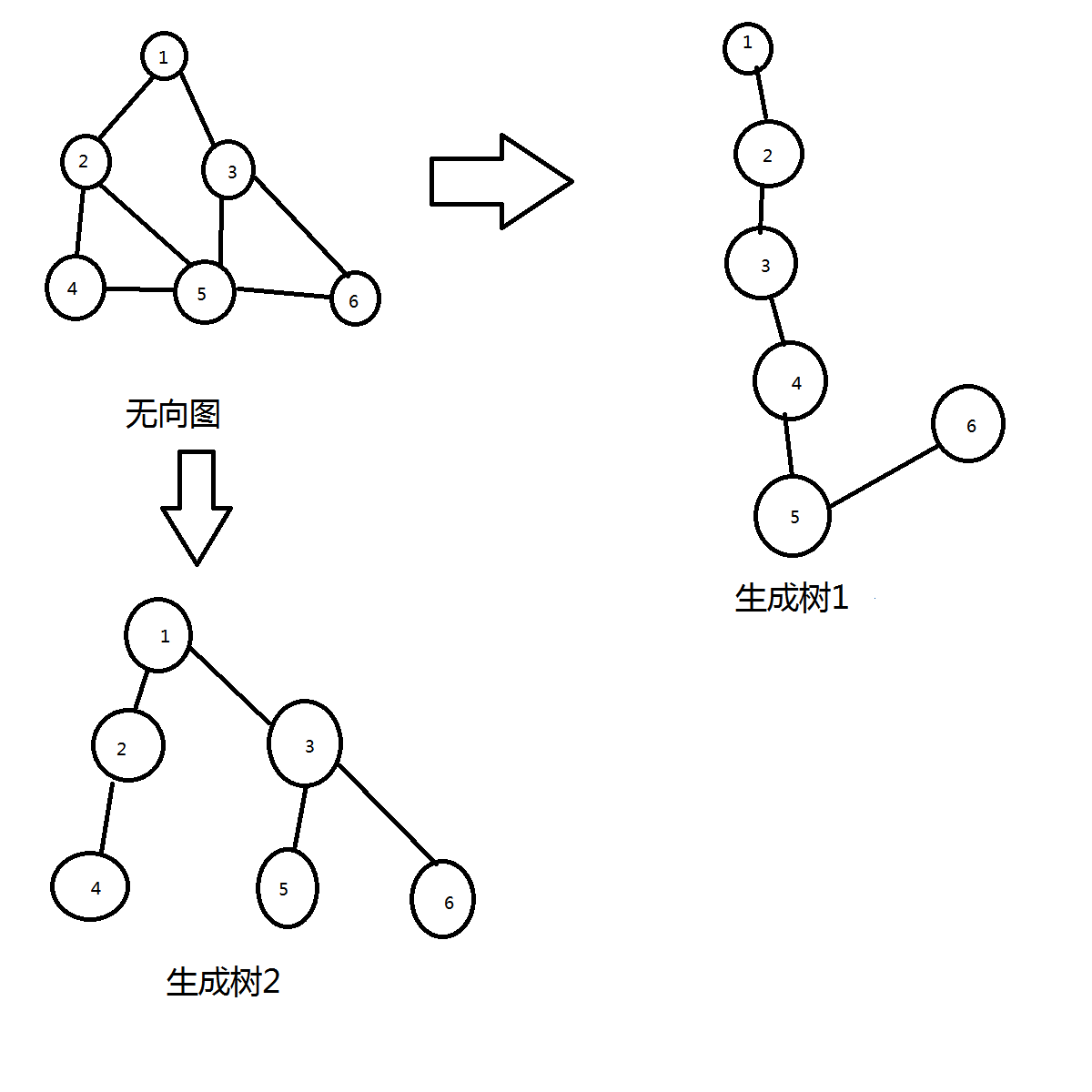
　　定理：任意一棵最小生成树一定包含无向图中权值最小的边。

　　在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得的 w(T) 最小，则此 T 为 G 的最小生成树。

　　　

　

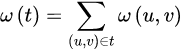
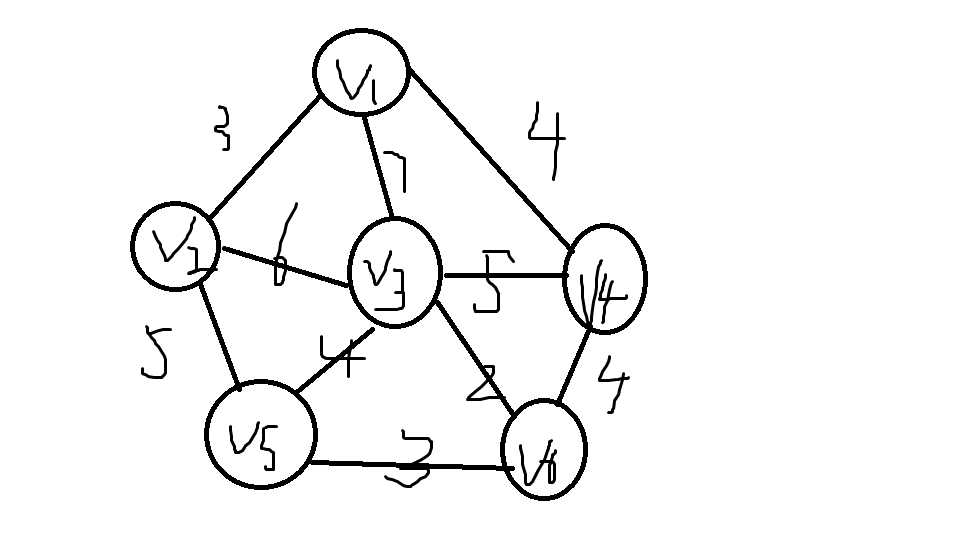
　　最小生成树其实是最小权重生成树的简称。

　　下面介绍两种算法：Kruskal和Prim。

　Kruskal是维护无向图的最小生成森林。Prim是维护最小生成树的一部分。

　　Kruskal：

　　1.建立并查集，以每个点为一个集合。

　　2.边权从小到大排序，扫描每条边（横坐标，纵坐标，边权）（下文用x，y，z分别表示）。

　　3.若x，y属于同一集合（就是所谓的联通），跳过，下一条。

　　4.如果不是，将其合并（这时候就用到了并查集），把z累加到答案中。

　　5.处理完所有边后，上一步处理的边就是最小生成树。

　　复杂度（o（m log m））；

　　核心代码：

　　

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;

struct rec{
    int x,y,z;
}edge[500010];

int fa[100010],n,m,ans;

bool operator <(rec a,rec b){
    return a.z<b.z;
}

int get(int x){
    if(x==fa[x]) return x;
    return fa[x]=get(fa[x]);
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++)
        scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].z);
    sort(edge+1,edge+m+1);//按边权排序 
    for(int i=1;i<=n;i++) fa[i]=i;//并查集初始化 
    for(int i=1;i<=m;i++){
        int x=get(edge[i].x);
        int y=get(edge[i].y);
        if(x==y) continue;
        fa[x]=y;
        ans+=edge[i].z; 
    }//求最小生成树 
    cout<<ans<<endl;
}

 

　　Prim：

　　最初，仅先确定1号节点属于最小生成树。任意时刻假设已经确定属于最小生成树的节点集合为T，剩余节点集合为S。Prim算法找到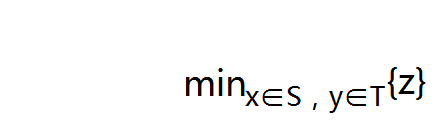，即两个端点分别属于集合S,T的权值最小的边，然后把点x从集合S中删除，加入到集合T，并把z累加到答案中。

　　具体一点，维护数组d：若x∈S，则d[x]表示节点x与集合T的节点之间权值最小的边的权值。若x∈T，则d[x]就等于x被加入T时选出的最小值的权值。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;

int a[3010][3010],d[3010],n,m,ans;
bool v[3010];

void prim(){
    memset(d,0x3f,sizeof(d));
    memset(v,0,sizeof(v));
    d[1]=0;
    for(int i=1;i<n;i++){
        int x=0;
        for(int j=1;j<=n;j++){
            if(!v[j]&&(x==0||d[j]<d[x])) x=j;
        v[x]=1;
        for(int y=1;y<=n;y++)
            if(!v[y]) d[y]=min(d[y],a[x][y]);
        }
    }
}

int main(){
    cin>>n>>m;
    memset(a,0x3f,sizeof(a));
    for(int i=1;i<=n;i++) a[i][i]=0;
    for(int i=1;i<=m;i++){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        a[y][x]=a[x][y]=min(a[x][y],z);
    }//建立邻接矩阵 
    prim();
    for(int i=2;i<=n;i++) ans+=d[i];//求最小生成树 
    cout<<ans<<endl;
}

两种方法不做比较，因题和个人而定。