棋盘问题

题目描述

设有一个N×M方格的棋盘(1≤N≤100,1≤M≤100)(1≤N≤100,1≤M≤100)

求出该棋盘中包含有多少个正方形、多少个长方形（不包括正方形）。

例如：当 N=2, M=3N=2,M=3时： 

正方形的个数有8个：即边长为1的正方形有6个；

边长为2的正方形有2个。

长方形的个数有10个：

即

2×1的长方形有4个 

1×2的长方形有3个： 

3×1的长方形有2个：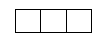 

3×2的长方形有1个：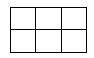 

如上例：输入：2,3

输出：8,10

这道题是入门难度，我真正想写的不是题解，而是自己的问题，一开始想判断每种情况，可是正方形写错了，就去看了看题解，发现有用公式的，自己举了几个数试了试，发现没有问题，自己就用了那个公式s1=(n-min(n,m)+1)*(m-min(n,m)+1)，s2=((1+n)*(1+m)*n*m)/4;在用s2-s1就是最后答案，有时候一些题其实可以用数学推导公式，用公式算就是公式不好想，要看情况而定。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,m,s1=0,s2;
    cin>>n>>m;
    s2=((m+1)*(n+1)*m*n)/4;
    for(;m>=1&&n>=1;m--,n--)
    s1+=m*n;                       
    cout<<s1<<" "<<s2-s1;
    return 0;
}