散列函数、消息摘要与数字签名

一， 散列函数（Hash function）

散列函数：任何一种能将任意大小数据映射为固定大小数据的函数，都能被称为散列函数。散列函数的返回值称为散列值、散列码，摘要或者简单散列。
也就是说散列函数能将任意长度的输入变换成固定长度的输出，该输出就是散列值。散列值空间通常远小于输入的空间。

散列函数的一些特性：

• 消息的长度不受限制
• 确定性：对于相同的输入（根据同一函数），它必须始终生成相同的散列值，如果两个散列值是不相同的，那么这两个散列值的原始输入也是不相同的， 但是对于不同的输入可能会散列成相同的输出（哈希碰撞），所以不可能从散列值来确定唯一的输入值。
• 均匀性：良好的散列函数应该输入尽可能均匀的映射到输出范围上。
• 单向性：在加密应用程序中，通常期望散列函数实际上是不可逆的。

二， 散列函数的应用

1. 散列表

散列函数通常与散列表（hash table）结合使用，使用散列表能够快速的按照关键字查找数据记录。具体地，散列函数会先将关键字映射到地址集合中的某一个位置，然后通过这个地址来查找数据记录（也就是将关键字通过散列函数转换的地址来查找表中的数据）

2. 加密散列函数

由于散列函数的多样性，它们经常是专门为某一应用而设计的，比如为加密和验证信息完整性而设计的散列函数（又被称为单向散列函数、杂凑函数或者消息摘要函数），这种散列函数是一个“单向”操作：对于给定的散列值，没有实用的方法可以计算出一个原始输入，也就是说很难伪造，比如 MD5 这种散列函数，被广泛用作检测文件的完整性。

2.1 验证消息的完整性

安全hash的一个重要应用就是验证消息的完整性：发送者将原文与摘要一起发送给接受者，然后接收者用同一个hash函数对收到的原文产生一个摘要，与发送者的摘要信息对比，如果相同，则说明收到的信息是完整的。
验证流程如下：

在上述流程中，信息收发双发在通信前已经商定了具体的散列算法，并且该算法是公开的，如果消息在传递过程中被篡改，则该消息不能与已获得的数字指纹相匹配。

2.2 单向散列函数（杂凑函数/消息摘要算法）

单向散列函数是一种特殊的散列函数，它是一种将任意长度的输入转换为固定长度的输出，但难以由输出转换成输入的散列函数。这个输出就被称为该消息（输入）的散列值，或者消息摘要。
就像前文所提到的，单向散列函数所保证的不是机密性，而是完整性。完整性指的是“数据是正牌的而不是伪造的”这一性质，使用单向散列函数，就可以检测出数据是否被篡改过。
（ps：一般地，把对一个消息的摘要称为该消息的指纹或者数字签名，它是一个唯一对应一消息或文本的固定长度的值，它由一个单向哈希函数对消息进行作用而产生。）

单向散列函数又称消息摘要算法，其核心在于散列函数的单向性。即通过散列函数可获得对应的散列值，但不可通过该散列值反推其原始信息。这是消息摘要算法的安全性的根本所在。

消息摘要算法的特征：
消息摘要算法就是前面所说的单向散列函数，它的主要特征就是加密过程中不需要密钥，并且经过加密的数据无法被破解，只有输入相同的明文数据经过相同的消息摘要算法才能得到相同的密文。消息摘要算法不存在密钥的管理与分发问题。

消息摘要算法能够验证消息的完整性（具体验证完整性的流程在上面已经介绍了），它主要应用在“数字签名”领域，作为对明文的摘要算法。

2.3 小结:

• 消息摘要算法是一种特殊的散列函数，因为具有单向性（即一个消息通过散列函数可获得其对应的散列值，但不可通过该散列值反推其原始信息），所以消息摘要算法也被称为单向散列函数。
• 消息摘要算法是验证数据完整性的算法
• 消息摘要算法返回的散列值通常也被称为 摘要 或者 数字签名。

3 数字签名

前面已经介绍了通过散列函数可以确保数据内容的完整性，但这还远远不够。此外，还需要确保数据来源的可认证性（身份识别）和数据发送行为的不可否认性（防止抵赖行为）。即完整性、可认证性和不可否认性。这些正是数字签名的主要特征。
任何一个公钥密码体制都可以单独作为一种数字签名方案使用，比如使用 RSA 作为数字签名方法使用时的流程如下：

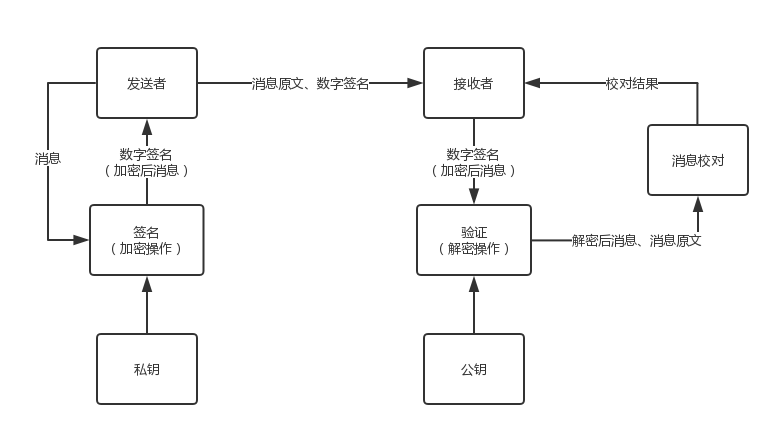
这种数字签名的流程是：发送方使用私钥对消息原文做签名（加密）处理，生成出消息原文的“数字签名”，然后将消息原文连同它的数字签名（即加密后的消息密文）一起发送给接收方。然后接收方使用公钥对接收到的消息密文做解密处理，并将公钥解密后的消息与原来的消息进行比较。
数字签名满足了以下的要求：

• 完整性：当使用公钥解密后的消息与消息原文相同，则说明消息是完整的，否则消息不完整
• 不可否认性和可认证性：当消息原文和加密后的消息密文一起被 A 发送给 接收方B 后，接收方B 可以确信信息确实是发送方A 发送的，同时 发送方A 也不能否认发送过该信息，因为除了 A 本人之外，其他任何人都无法由消息原文产生正确的消息密文，所以 RSA 数字签名方案是可行的。

但是这种方案是存在问题的，这种方案需要对所有信息原文进行加密操作，这在消息的长度比较大时，效率是非常低的，主要原因在于公钥体质的加解密过程的低效性，所以这种方案通常不可取。

3.1 更有效的数字签名算法

这种数字签名算法可以看做是一种带有密钥的消息摘要算法，并且这种密钥包含了公钥和私钥，也就是说，数字签名算法是非对称加密算法和消息摘要算法的结合体。
具体流程如下：

1. 发送方先用摘要算法对消息进行摘要（digest），加密后的密文被称作摘要。
2. 发送方把摘要用私钥进行加密，生成“数字签名”（signature）
3. 发送方将 数字签名 和消息原文 一起发送给接收方
4. 接收方使用相同的散列函数从接收到的消息原文中计算出摘要1
5. 接收方使用公钥对数字签名进行解密得到摘要2。
6. 比较摘要1和摘要2是否相等，如果相等，则就能确定消息的完整性以及消息的来源确实是发送方

几乎所有的数字签名方法都要和快速高效的摘要算法（hash函数）一起使用，当非对称加密算法和消息摘要算法结合起来使用，便构成了一种有效地数字签名方案。比如当经典的非对称加密算法和数字签名算法——RSA 算法与消息摘要算法 MD5 结合之后就形成了MD5withRSA 算法。

参考：
百度百科: https://baike.baidu.com/item/数字签名
wiki百科: https://en.wikipedia.org/wiki/Hash_function
Java加密与解密的艺术