分箱——转
one-hot 编码会将原始变量中的每个状态都做为作为一个新的特征,当原始特征状态较多时,数据经过one-hot编码之后特征数量会成倍的增加,同时新特征也会变得过于稀疏。在进行变量筛选的过程中,也会出现原始特征的一部分状态被筛选出来,另一部分状态未被筛选出来,造成特征的不完整。
而WOE编码不仅可以解决以上这些问题,同时还可以将特征转化为线性。
在建模中,需要对连续变量离散化,特征离散化后,模型会更稳定,降低了模型过拟合的风险。
一、有监督的卡方分箱法(ChiMerge)
自底向上的(即基于合并的)数据离散化方法。
它依赖于卡方检验:具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。
基本思想:
对于精确的离散化,相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布,则这两个区间可以合并;否则,它们应当保持分开。而低卡方值表明它们具有相似的类分布。
我们先来看看卡方分布的定义:
若kk个独立的随机变量Z1,Z2,⋯,Zk且符合标准正态分布N(0,1),则这kk个随机变量的平方和

χ2检验是以χ2分布为基础的一种假设检验方法,主要用于分类变量。其基本思想是根据样本数据推断总体的分布与期望分布是否有显著性差异,或者推断两个分类变量是否相关或者独立。
一般可以设原假设为 H0:观察频数与期望频数没有差异,或者两个变量相互独立不相关。
实际应用中,我们先假设H0成立,计算出χ2的值,χ2表示观察值与理论值之间的偏离程度。根据χ2分布,χ2统计量以及自由度,可以确定在H0成立的情况下获得当前统计量以及更极端情况的概率p。
如果p很小,说明观察值与理论值的偏离程度大,应该拒绝原假设。否则不能拒绝原假设。
实际上WOE编码相当于把分箱后的特征从非线性可分映射到近似线性可分的空间内。如下图所示:
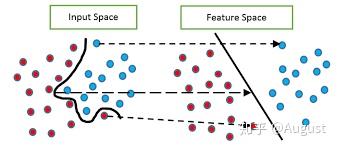
总结一下WOE编码的优势:
- 可提升模型的预测效果
- 将自变量规范到同一尺度上
- WOE能反映自变量取值的贡献情况
- 有利于对变量的每个分箱进行评分
- 转化为连续变量之后,便于分析变量与变量之间的相关性
- 与独热向量编码相比,可以保证变量的完整性,同时避免稀疏矩阵和维度灾难



