图论基本知识
图
图的基本概念
图示一个复杂的结构,节点之间的关系可以是任意的,图中的任意两个元素之间都可能相关。
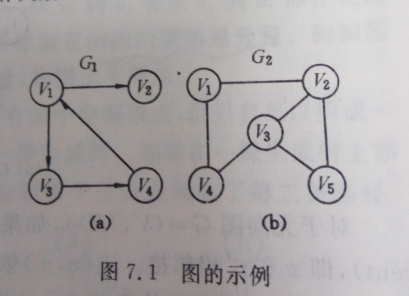
图分为有向图和无向图,无向图为两个节点之间互相可以到达,有向图只能根据箭头所指的方向到达另一个节点。上图中(a)为有向图,(b)为无向图
有时边或者弧具有与它相关的数,这种数字叫做权,这种带权的图常常称为网。
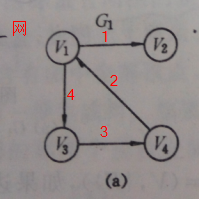
回路:第一个顶点和最后一个顶点相同的路径称之为回路或者环,路径中顶点不重复出现为简单路径,回路中无重复顶点为简单回路。
连通:如果两个顶点之间有路径,则称这两个顶点是连通的,如果图中的任意一点都可以到其他的所有顶点,则称这个图为连通图。
连通分量:无向图中的极大连通子图(N个顶点构成一个连通图),连通图必然有连通分量,有连通分量不一定为连通图,两者无必然联系。
有向图的连通图成为强连通图和强连通子图,概念和无向图的相同
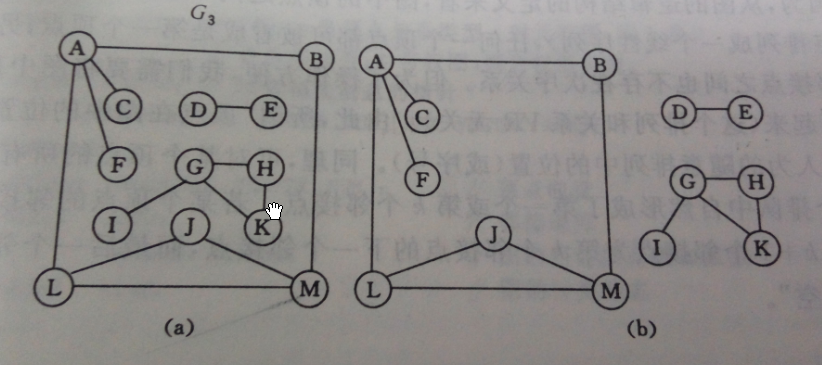
图的存储结构
邻接矩阵
用矩阵来存储图的结构

0表示两个顶点之间无联系,1表示有联系(无向图中由于没有方向所以V3可以到达V2 V2也可以到达V3)
构建邻接矩阵
import java.util.Scanner;
public class UDN {
String vex[] = new String[100]; // 邻接矩阵
int a[][]; // 顶点存储数组
// 创建邻接矩阵
public void createChart() {
int i = 0;
int t = 0;
Scanner in = new Scanner(System.in);
System.out.println("请输入顶点");
String str = in.nextLine();
while (str.length() != 0) {
vex[t] = str;
t++;
str = in.nextLine();
}
System.out.println(t);
a = new int[t][t]; // 邻接矩阵
for (i = 0; i < t; i++) {
System.out.println("请输入一条边的依附顶点");
String d1 = in.nextLine();
String d2 = in.nextLine();
int d1Index = findLine(d1);
int d2Index = findLine(d2);
a[d2Index][d1Index] = 1;
a[d1Index][d2Index] = 1;
}
}
// 输出
public void print() {
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a.length; j++) {
System.out.print(a[i][j] + " ");
}
System.out.println();
}
}
// 查找输入顶点对应的下标
public int findLine(String d1) {
int i = 0;
for (int t = 0; t < vex.length; t++) {
if (vex[t].equals(d1)) {
i = t;
break;
}
}
return i;
}
public static void main(String[] args) {
UDN i = new UDN();
i.createChart();
i.print();
}
}
邻接表存储
邻接表是一种链式的存储结构,存储结构示意图(a):
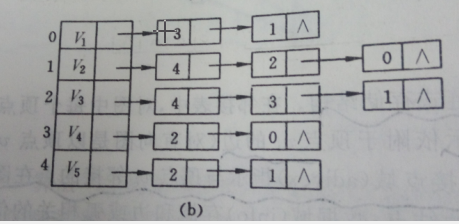
数组中存储的为节点,每个节点后面为此节点邻接节点的下标
头节点
public class VNode {
private String data; // 该弧的顶点信息
private ArcNode firstArc; // 第一条弧
public String getData() {
return data;
}
public void setData(String data) {
this.data = data;
}
public ArcNode getFirstArc() {
return firstArc;
}
public void setFirstArc(ArcNode firstArc) {
this.firstArc = firstArc;
}
}
表节点
public class VNode {
private String data; // 该弧的顶点信息
private ArcNode firstArc; // 第一条弧
public String getData() {
return data;
}
public void setData(String data) {
this.data = data;
}
public ArcNode getFirstArc() {
return firstArc;
}
public void setFirstArc(ArcNode firstArc) {
this.firstArc = firstArc;
}
}
图的信息
public class AlGraph {
private VNode nodeList[];
private int vexnum, arcnum; // 图的定点数和弧数
private int kind; // 弧的种类
public VNode[] getNodeList() {
return nodeList;
}
public void setNodeList(VNode[] nodeList) {
this.nodeList = nodeList;
}
public int getVexnum() {
return vexnum;
}
public void setVexnum(int vexnum) {
this.vexnum = vexnum;
}
public int getArcnum() {
return arcnum;
}
public void setArcnum(int arcnum) {
this.arcnum = arcnum;
}
public int getKind() {
return kind;
}
public void setKind(int kind) {
this.kind = kind;
}
}
构建
public class AdjancecyListDemo {
AlGraph alGraph = new AlGraph();
public void createAdjancency() {
Scanner in = new Scanner(System.in);
System.out.println("请输入顶点数");
int n = in.nextInt(); // 表内容初始化
alGraph.setNodeList(new VNode[n]);
alGraph.setVexnum(n);
System.out.println("请输入弧数");
alGraph.setArcnum(in.nextInt());
VNode[] list = alGraph.getNodeList(); // 头结点初始化
System.out.println(list.length);
System.out.println("input Node:");
for (int i = 0; i < list.length; i++) {
VNode node = new VNode();
node.setData(in.next());
list[i] = node;
}
for (int i = 0; i < alGraph.getArcnum(); i++) {
System.out.println("请输入弧依附的两个顶点"); // 构建邻接表
String begin = in.next();
String end = in.next();
int ii = findIndex(begin);
int jj = findIndex(end);
if (ii == -1 || jj == -1) {
System.out.println("输入的节点不存在");
return;
}
ArcNode arcNode = new ArcNode();
addArcNode(ii, jj, end);
addArcNode(jj, ii, begin);
}
}
public void prinfAlGralph() { // 输出
VNode[] list = alGraph.getNodeList();
for (int i = 0; i < list.length; i++) {
System.out.print(i + "-" + list[i].getData() + " : ");
ArcNode arc = list[i].getFirstArc();
while (arc != null) {
System.out.print(arc.getAdjVex() + " | ");
arc = arc.getNextArc();
}
System.out.println();
}
}
public void addArcNode(int index, int end, String info) { // 添加表结点
VNode[] list = alGraph.getNodeList();
ArcNode tempArc = list[index].getFirstArc();
ArcNode arcNode = new ArcNode();
if (tempArc == null) {
arcNode.setAdjVex(end);
arcNode.setInfo(info);
list[index].setFirstArc(arcNode);
} else {
while (tempArc.getNextArc() != null) {
tempArc = tempArc.getNextArc();
}
arcNode.setAdjVex(end);
arcNode.setInfo(info);
tempArc.setNextArc(arcNode);
}
}
public int findIndex(String node) { // 查找给定节点的下标
VNode[] list = alGraph.getNodeList();
for (int i = 0; i < list.length; i++) {
if (list[i].getData().equals(node)) {
return i;
}
}
return -1;
}
public static void main(String[] args) {
AdjancecyListDemo demo = new AdjancecyListDemo();
demo.createAdjancency();
demo.prinfAlGralph();
}
}




