BP神经网络模型

1. BP神经网络模型（Backpropagation Neural Networks）

• 采用非线性激活函数，Sigmoid函数。
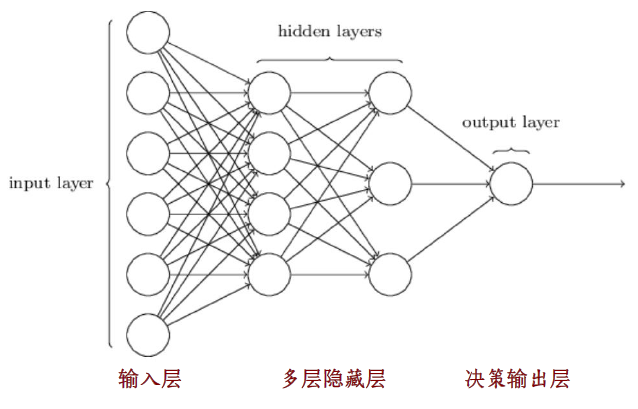
• 三个层次：输入层（Input Layer）,隐藏层（Hidden Layer） 和输出层（Output layer），就好比神经网络的各个神经元具有不同功能一样。
• 输入层：负责接收外界刺激，即外部数据。
• 隐藏层：又叫可多层，负责增加计算能力，以解决困难问题。但隐藏层神经元不能无限增加，否则会出现过拟合现象。
• 输出层：又称为决策层，负责进行决策。
• 一般来说，当数据和决策问题确定之后，输入层和输出层的节点个数是固定的，唯一可变的是隐藏层。
• 层与层之间是通过神经键（权重）完成连接。
• 训练好之后的BP神经网路模型是前馈的（feedforward），但在进行模型训练的时候是从输出层到输入层，是反馈的（即：Train Backward）

• • （图片来源：经管之家CDA）

 

2.如何构建BP神经网络

　　（1） 只有隐藏层和输出层的神经元才有构造，且每个神经元的 构造都是一模一样的，而输入层的神经元只负责接收外来数据，数据一旦输入，便会立即输出，故不具有构造。

　　（2）神经元由上一层神经元与本层神经元交叉形成神经键、权重加总（Weighted Sum）、常数项（Bias）以及激活函数（Activation Function）组成。

　　（3）w0j,w1j,...wnj 表示上一层神经元对于该神经元的影响权重Weights，可正可负，范围为【0,1】；常数项（Bias）表示神经元自身的偏好；激活函数f表示一个以权重加总和常数项之和为自变量的函数，决定该神经元的输出结果。

　　

 

 　　（4）在BP神经网络中，一般采用S型函数作为激活函数。表达式为1/(1+e^-xj)，其中xj 是权重加总和常数项之和，成为组合函数的值，当组合函数的值为负时，激活函数的值小于0.5，否则，激活函数的值大于0.5。

 

3.应用举例

　　

 

 　　（1）假设训练数据（x1，x2，x3）为（1,0,1），各个神经键的权重值以及隐藏层和输出层神经元的常数项随机取值如下

 

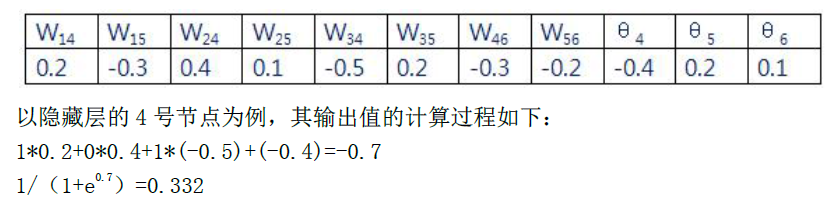
 　　（2）同理，计算出4/5/6节点的输出值依次为：0.332，0.525,0.474

　　　　

 

 

　　 （3）假设实际的结果应当为 1 ，但采用随机赋予权重值的方法得到输出值为0.474，与目标值1 差距过大，因而要对神经网络进行修正。

　　（4）修正权重和常数项值需要一个标准：平方误差。平方误差=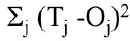，其中，Tj为训练数据实际值，Oj为神经网络输出值。

 

　　（5）新的权重值=旧的权重值+学习效率*前节点的输出值*后节点的误差值。