509. 斐波那契数

509. 斐波那契数

暴力破解

class Solution {
    public int fib(int n) {
        //data base
        if(n == 0 || n==1){
            return n;
        } 
        //递推关系
        return fib(n-1)+fib(n-2);

    }
}

时间复杂度

递归函数本身的复杂度是：O(1),里面没有循环

递归函数调用的次数就是递归树的结点，如下图

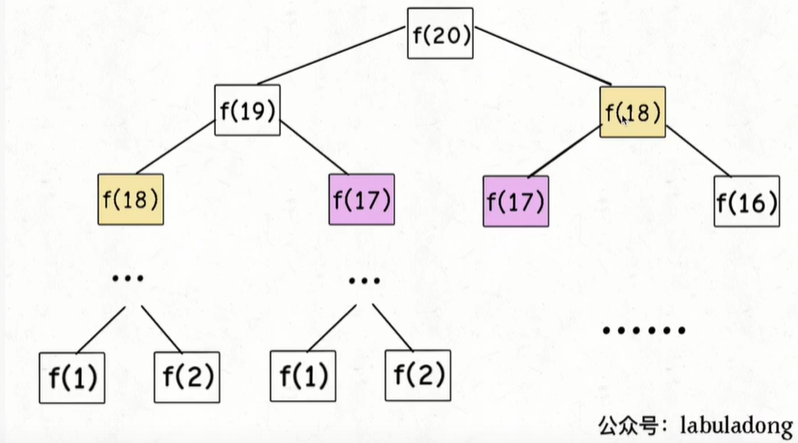
递归次数是高度为n的二叉树的结点个数：2的n次方

所以上面所写的暴力算法是时间复杂度就是：O(1)xO(2^n) = O(2^n)，所以效率非常低。

带备忘录的递归算法（自顶向下）

class Solution {

    public int fib(int N) {
        //备忘录全初始化为0
        int[] memo = new int[N+1];
        return helper(memo,N);
    }

    private int helper(int[] memo,int n){
        //base case
        if(n == 0 ||n==1) return n;        
        //已经计算过了，不用再计算了
        if(memo[n]!= 0)return memo[n];                 
        memo[n] = helper(memo,n-1)+helper(memo,n-2);
        return memo[n];
    }
}

时间复杂度

O(n)x O(1) = O(n)

将树形时间复杂度度转换成链性事件复杂度，用空间换取时间。

递推解法（自底向上）

• 使用了dp数组

class Solution {

    public int fib(int N) {
       if(N==0) return 0;
       int[] dp = new int[N+1];
       //base case
       dp[0] = 0;dp[1] = 1;
       //状态转移
       for(int i=2;i<=N;i++){
           dp[i] = dp[i-1]+dp[i-2];
       }
       return dp[N];
    
    }

}

其实,dp数组里面存的内容和memo是完全一样的，只不过把递归改为了for循环迭代了而已。

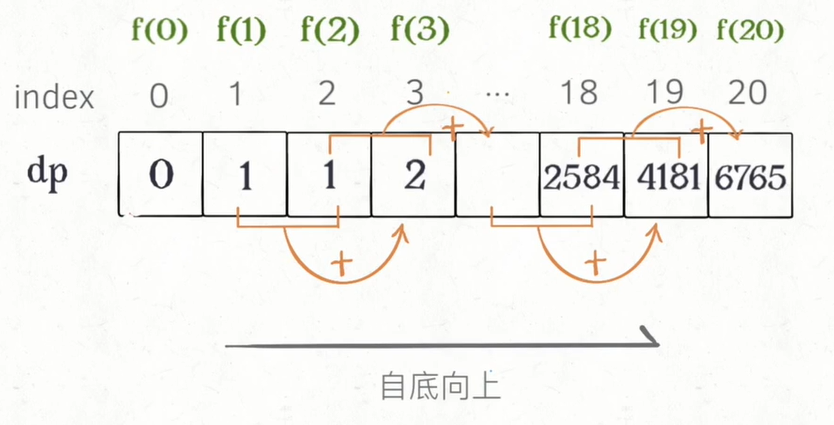
空间复杂度和时间复杂度最优的解法

上面两个最优解法，本质都是保存一个大小为N的数组，但实际上，每个值都是满足关系的也就是F(n) = F(n - 1) + F(n - 2),我们可以把空间再进行优化。保留两个数字就可以。

class Solution {

    public int fib(int n) {
        //base case
        if(n==0 || n==1)
            return n;        
        int prev = 0, curr =1;

        for(int i = 2; i <= n; i++){
            int sum = prev + curr;
            prev = curr;
            curr = sum;
        }
        return curr;
    }
       
}